sklearn.linear model.LinearRegression: Difference between revisions
m (Remove links to pages that are actually redirects to this page.) |
m (Remove links to pages that are actually redirects to this page.) |
||
| Line 28: | Line 28: | ||
:x = boston.data <span style="font-weight:italic; color:gray;># Creating Regression Design Matrix </span> | :x = boston.data <span style="font-weight:italic; color:gray;># Creating Regression Design Matrix </span> | ||
:y = boston.target <span style="font-weight:italic; color:gray;># Creating target dataset</span> | :y = boston.target <span style="font-weight:italic; color:gray;># Creating target dataset</span> | ||
:linreg = [[LinearRegression()]] <span style="font-weight:italic; color:gray;># Create linear regression object </span> | :linreg = [[sklearn.linear model.LinearRegression|LinearRegression()]] <span style="font-weight:italic; color:gray;># Create linear regression object </span> | ||
:linreg.fit(x,y) <span style="font-weight:italic; color:gray; # Fit linear regression</span> | :linreg.fit(x,y) <span style="font-weight:italic; color:gray; # Fit linear regression</span> | ||
:yp = linreg.predict(x) <span style="font-weight:italic; color:gray;># predicted values</span> | :yp = linreg.predict(x) <span style="font-weight:italic; color:gray;># predicted values</span> | ||
Revision as of 20:45, 23 December 2019
A sklearn.linear model.LinearRegression is a linear least-squares regression system within sklearn.linear_model class.
- AKA: LinearRegression, linear model.LinearRegression
- Context
- Usage:
- 1) Import Linear Regression model from scikit-learn :
from sklearn.linear_model import LinearRegression - 2) Create a design matrix
Xand response vectorY - 3) Create a Lasso Regression object:
model=LinearRegression([fit_intercept=True, normalize=False, copy_X=True, n_jobs=1]) - 4) Choose method(s):
- Fit model with coordinate descent:
model.fit(X, Y[, check_input]))(supervised learning) ormodel.fit(X)(unsupervised learning) - Predict Y using the linear model with estimated coefficients:
Y_pred = model.predict(X) - Return coefficient of determination (R^2) of the prediction:
model.score(X,Y[, sample_weight=w]) - Get estimator parameters:
model.get_params([deep]) - Set estimator parameters:
model.set_params(**params)
- Fit model with coordinate descent:
- 1) Import Linear Regression model from scikit-learn :
- Example(s):
| Input: | Output: |
|
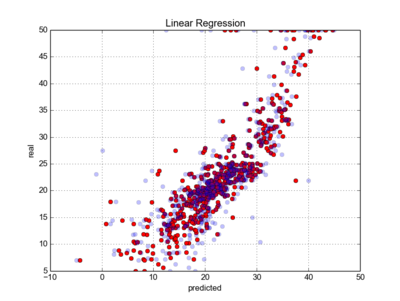
|
|
#Calculaton of RMSE and Explained Variances
|
|
- Counter-Example(s)
- See: Linear Regression Task, Ordinary Least Squares Linear Regression System, Estimation Task, Coordinate Descent Algorithm.
References
2017a
- http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
- QUOTE: Ordinary least squares Linear Regression.
class sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)[source]
- QUOTE: Ordinary least squares Linear Regression.
2017b
# Split the targets into training/testing sets diabetes_y_train = diabetes.target[:-20] diabetes_y_test = diabetes.target[-20:]
# Create linear regression object regr = linear_model.LinearRegression()
# Train the model using the training sets regr.fit(diabetes_X_train, diabetes_y_train)
2017D
- (Mobasher,2017) ⇒ Bamshad Mobasher (2017). Example of Regression Analysis Using the Boston Housing Data Set. Retrieved 2017-10-01
2017 e.
- (Scipy Lectures, 2017) ⇒ http://www.scipy-lectures.org/packages/scikit-learn/#supervised-learning-regression-of-housing-data
- QUOTE: 3.6.4.2. Predicting Home Prices: a Simple Linear Regression
Now we'll use scikit-learn to perform a simple linear regression on the housing data. There are many possibilities of regressors to use. A particularly simple one is LinearRegression: this is basically a wrapper around an ordinary least squares calculation.
- QUOTE: 3.6.4.2. Predicting Home Prices: a Simple Linear Regression
| from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(data.data, data.target) from sklearn.linear_model import LinearRegression clf = LinearRegression() clf.fit(X_train, y_train) predicted = clf.predict(X_test) expected = y_test print("RMS: %s" % np.sqrt(np.mean((predicted - expected) ** 2))) |
- We can plot the error: expected as a function of predicted:
plt.scatter(expected, predicted)
2016
- (Thiebaut) ⇒ D. Thiebaut (2016). SKLearn Tutorial: Linear Regression on Boston Data