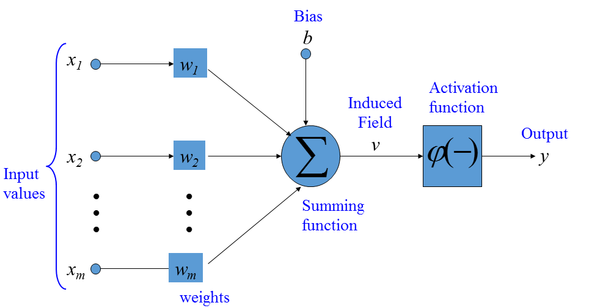
Artificial Neuron
An Artificial Neuron is a computational unit that can model a biological neuron (by processing artificial neuron inputs to produce artificial neuron outputs).
- AKA: Neural Network Node, Neural Network Unit, Neural Network Processing Element, Virtual Neuron, Computational Neuron.
- Context:
- It can typically receive multiple artificial neuron inputs through artificial neural connections.
- It can typically compute weighted sums of artificial neuron inputs using neural network weights.
- It can typically apply neuron activation functions to produce artificial neuron outputs.
- It can typically be connected to other artificial neurons via artificial neural connections within an artificial neural network.
- It can typically serve as a graph node within an artificial neural network topology.
- ...
- It can often learn neural network patterns through artificial neuron training algorithms.
- It can often adjust neural network weights during artificial neuron training processes.
- It can often contribute to artificial neural network computations for pattern recognition tasks.
- It can often model synaptic plasticity through weight modification mechanisms.
- ...
- It can range from being a Visible Artificial Neuron to being a Hidden Artificial Neuron, depending on its artificial neuron layer position.
- It can range from being an Artificial Neuron Instance to being an Abstract Artificial Neuron, depending on its artificial neuron implementation level.
- It can range from being a Linear Artificial Neuron to being a Nonlinear Artificial Neuron, depending on its artificial neuron activation function.
- It can range from being a Deterministic Artificial Neuron to being a Stochastic Artificial Neuron, depending on its artificial neuron output behavior.
- ...
- It can be produced by an Artificial Neuron Training Task that can be solved by an Artificial Neuron Training System implementing an Artificial Neuron Training Algorithm.
- It can be mathematically described by a Single Layer Artificial Neural Network Model containing only 1 Neuron:
[math]\displaystyle{ y=f( \displaystyle\sum_{i=1}^n w_i x_i+b) }[/math]
where [math]\displaystyle{ f }[/math] is the Neural Activation Function, [math]\displaystyle{ x }[/math] is the Neuron Input Vector, [math]\displaystyle{ y }[/math] is the Neuron Output Vector, [math]\displaystyle{ w_i }[/math] is the Neural Network Weights, [math]\displaystyle{ b }[/math] is the Bias Neuron.
- It can be graphically represented as:
- It can process artificial neural signals analogous to biological neural signals in biological neurons.
- It can exhibit artificial neuron behaviors such as neuron firing when activation thresholds are exceeded.
- ...
- Example(s):
- Linear Neuron Types, such as:
- Identity Neuron, which applies identity activation function.
- Parametric Linear Neuron, which uses parametric linear activation function.
- Sigmoid-based Neuron Types, such as:
- Logistic Sigmoid Neuron, which uses logistic sigmoid activation function.
- Hyperbolic Tangent Neuron, which applies hyperbolic tangent activation function.
- Rectifier-based Neuron Types, such as:
- Rectified Linear Unit (ReLU), which implements ReLU activation function.
- Leaky ReLU Neuron, which uses leaky ReLU activation function.
- Parametric ReLU Neuron, which applies parametric ReLU activation function.
- Step Function Neuron Types, such as:
- Heaviside Step Neuron, which implements Heaviside step activation function.
- Binary Threshold Neuron, which uses binary threshold activation function.
- Probabilistic Neuron Types, such as:
- Stochastic Binary Neuron, which exhibits stochastic firing behavior.
- Gaussian Neuron, which uses Gaussian activation function.
- Specialized Neuron Types, such as:
- Softmax Neuron, for multi-class classification tasks.
- Maxout Neuron, which implements maxout activation function.
- Sinusoidal Neuron, which uses sinusoidal activation function.
- Historical Neuron Models, such as:
- McCulloch-Pitts Neuron (1943), the first artificial neuron model.
- Perceptron Neuron (1958), for binary classification tasks.
- ADALINE Neuron (1960), with adaptive linear elements.
- ...
- Linear Neuron Types, such as:
- Counter-Example(s):
- Biological Neurons, which are living cells with biological processes rather than mathematical functions.
- Bias Neurons, which provide constant bias values rather than processing variable inputs.
- Neural Network Weights, which are connection parameters rather than processing units.
- Neural Network Layers, which are neuron collections rather than individual processing elements.
- Activation Functions, which are mathematical transformations rather than complete neuron models.
- Example(s):
- See: Artificial Neural Network, MCP Neuron Model, Artificial Neuron, Fully-Connected Neural Network Layer, Neuron Activation Function, Neural Network Weight, Neural Network Connection, Neural Network Topology, Multi Hidden Layer NNet.
References
2018
- (CS231n, 2018) ⇒ Biological motivation and connections. In: CS231n Convolutional Neural Networks for Visual Recognition Retrieved: 2018-01-14.
- QUOTE: The basic computational unit of the brain is a neuron. Approximately 86 billion neurons can be found in the human nervous system and they are connected with approximately [math]\displaystyle{ 10^{14} - 10^{15} }[/math] synapses. The diagram below shows a cartoon drawing of a biological neuron (left) and a common mathematical model (right). Each neuron receives input signals from its dendrites and produces output signals along its (single) axon. The axon eventually branches out and connects via synapses to dendrites of other neurons. In the computational model of a neuron, the signals that travel along the axons (e.g. [math]\displaystyle{ x_0 }[/math]) interact multiplicatively (e.g. [math]\displaystyle{ w_0x_0 }[/math]) with the dendrites of the other neuron based on the synaptic strength at that synapse (e.g. [math]\displaystyle{ w_0 }[/math]). The idea is that the synaptic strengths (the weights [math]\displaystyle{ w }[/math]) are learnable and control the strength of influence (and its direction: excitory (positive weight) or NN Inhibitoryinhibitory (negative weight) of one neuron on another. In the basic model, the dendrites carry the signal to the cell body where they all get summed. If the final sum is above a certain threshold, the neuron can fire, sending a spike along its axon. In the computational model, we assume that the precise timings of the spikes do not matter, and that only the frequency of the firing communicates information. Based on this rate code interpretation, we model the firing rate of the neuron with an activation function [math]\displaystyle{ f }[/math], which represents the frequency of the spikes along the axon. Historically, a common choice of activation function is the sigmoid function [math]\displaystyle{ \sigma }[/math], since it takes a real-valued input (the signal strength after the sum) and squashes it to range between 0 and 1. We will see details of these activation functions later in this section.
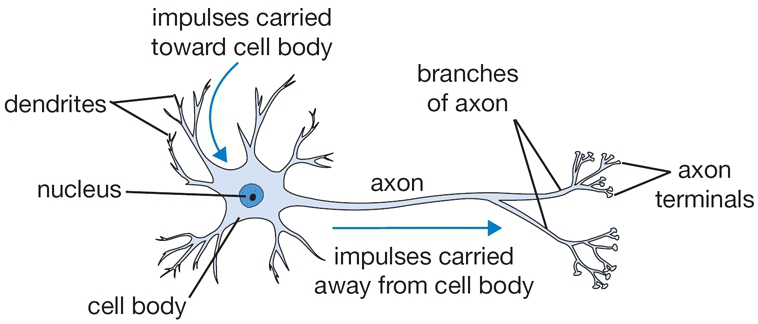
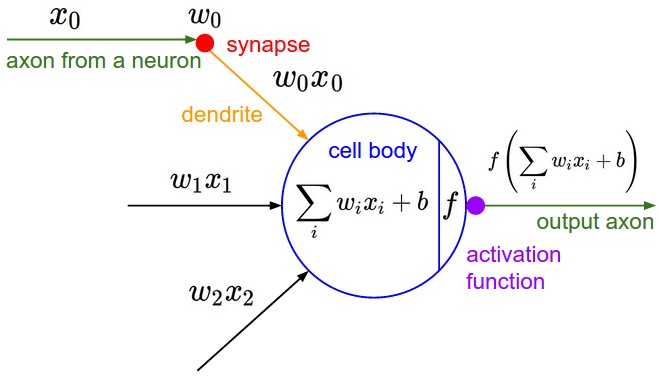
A cartoon drawing of a biological neuron (left) and its mathematical model (right).
- QUOTE: The basic computational unit of the brain is a neuron. Approximately 86 billion neurons can be found in the human nervous system and they are connected with approximately [math]\displaystyle{ 10^{14} - 10^{15} }[/math] synapses. The diagram below shows a cartoon drawing of a biological neuron (left) and a common mathematical model (right). Each neuron receives input signals from its dendrites and produces output signals along its (single) axon. The axon eventually branches out and connects via synapses to dendrites of other neurons. In the computational model of a neuron, the signals that travel along the axons (e.g. [math]\displaystyle{ x_0 }[/math]) interact multiplicatively (e.g. [math]\displaystyle{ w_0x_0 }[/math]) with the dendrites of the other neuron based on the synaptic strength at that synapse (e.g. [math]\displaystyle{ w_0 }[/math]). The idea is that the synaptic strengths (the weights [math]\displaystyle{ w }[/math]) are learnable and control the strength of influence (and its direction: excitory (positive weight) or NN Inhibitoryinhibitory (negative weight) of one neuron on another. In the basic model, the dendrites carry the signal to the cell body where they all get summed. If the final sum is above a certain threshold, the neuron can fire, sending a spike along its axon. In the computational model, we assume that the precise timings of the spikes do not matter, and that only the frequency of the firing communicates information. Based on this rate code interpretation, we model the firing rate of the neuron with an activation function [math]\displaystyle{ f }[/math], which represents the frequency of the spikes along the axon. Historically, a common choice of activation function is the sigmoid function [math]\displaystyle{ \sigma }[/math], since it takes a real-valued input (the signal strength after the sum) and squashes it to range between 0 and 1. We will see details of these activation functions later in this section.
2017
- (Miikkulainen, 2011c) ⇒ Miikkulainen R. (2017) Neuron. In: Sammut, C., Webb, G.I. (eds) Encyclopedia of Machine Learning and Data Mining. Springer, Boston, MA.
- QUOTE: Neurons carry out the computational operations of a network; together with connections (see Topology of a Neural Network, Weight), they constitute the neural network. Computational neurons are highly abstracted from their biological counterparts. In most cases, the neuron forms a weighted sum of a large number of inputs (activations of other neurons), applies a nonlinear transfer function to that sum, and broadcasts the resulting output activation to a large number of other neurons. Such activation models the firing rate of the biological neuron, and the nonlinearity is used to limit it to a certain range (e.g., 0 or 1 with a threshold, (0, 1) with a sigmoid, (− 1, 1) with a hyperbolic tangent, or (0, ∞) with an exponential function). Each neuron may also have a bias weight, i.e., a weight from a virtual neuron that is always maximally activated, which the learning algorithm can use to adjust the input sum quickly into the most effective range of …
2016a
- (Wikipedia, 2016) ⇒ https://en.wikipedia.org/wiki/artificial_neuron Retrieved:2016-8-5.
- An artificial neuron is a mathematical function conceived as a model of biological neurons. Artificial neurons are the constitutive units in an artificial neural network. Depending on the specific model used they may be called a semi-linear unit, Nv neuron, binary neuron, linear threshold function, or McCulloch–Pitts (MCP) neuron. The artificial neuron receives one or more inputs (representing dendrites) and sums them to produce an output (representing a neuron's axon). Usually the sums of each node are weighted, and the sum is passed through a non-linear function known as an activation function or transfer function. The transfer functions usually have a sigmoid shape, but they may also take the form of other non-linear functions, piecewise linear functions, or step functions. They are also often monotonically increasing, continuous, differentiable and bounded. The thresholding function is inspired to build logic gates referred to as threshold logic; with a renewed interest to build logic circuit resembling brain processing. For example, new devices such as memristors have been extensively used to develop such logic in the recent times.
The artificial neuron transfer function should not be confused with a linear system's transfer function.
- An artificial neuron is a mathematical function conceived as a model of biological neurons. Artificial neurons are the constitutive units in an artificial neural network. Depending on the specific model used they may be called a semi-linear unit, Nv neuron, binary neuron, linear threshold function, or McCulloch–Pitts (MCP) neuron. The artificial neuron receives one or more inputs (representing dendrites) and sums them to produce an output (representing a neuron's axon). Usually the sums of each node are weighted, and the sum is passed through a non-linear function known as an activation function or transfer function. The transfer functions usually have a sigmoid shape, but they may also take the form of other non-linear functions, piecewise linear functions, or step functions. They are also often monotonically increasing, continuous, differentiable and bounded. The thresholding function is inspired to build logic gates referred to as threshold logic; with a renewed interest to build logic circuit resembling brain processing. For example, new devices such as memristors have been extensively used to develop such logic in the recent times.
2016b
- (Zhao, 2016) ⇒ Peng Zhao, February 13, 2016. R for Deep Learning (I): Build Fully Connected Neural Network from Scratch
- QUOTE: A neuron is a basic unit in the DNN which is biologically inspired model of the human neuron. A single neuron performs weight and input multiplication and addition (FMA), which is as same as the linear regression in data science, and then FMA’s result is passed to the activation function. The commonly used activation functions include sigmoid, ReLu, Tanh and Maxout. In this post, I will take the rectified linear unit (ReLU) as activation function, f(x) = max(0, x). For other types of activation function, you can refer here.
(...)
In R, we can implement neuron by various methods, such as
sum(xi*wi). But, more efficient representation is by matrix multiplication.R code:
neuron.ij <- max(0, input %*% weight + bias)
- QUOTE: A neuron is a basic unit in the DNN which is biologically inspired model of the human neuron. A single neuron performs weight and input multiplication and addition (FMA), which is as same as the linear regression in data science, and then FMA’s result is passed to the activation function. The commonly used activation functions include sigmoid, ReLu, Tanh and Maxout. In this post, I will take the rectified linear unit (ReLU) as activation function, f(x) = max(0, x). For other types of activation function, you can refer here.
2016c
- (Garcia et al., 2016) ⇒ García Benítez, S. R., López Molina, J. A., & Castellanos Pedroza, V. (2016). Neural networks for defining spatial variation of rock properties in sparsely instrumented media. Boletín de la Sociedad Geológica Mexicana, 68(3), 553-570.
- QUOTE: Since the first neural model by McCulloch and Pitts (1943), hundreds of different models have been developed. Given that the function of ANNs is to process information, they are used mainly in fields related to this topic. The wide variety of ANNs used for engineering purposes works mainly in pattern recognition, forecasting, and data compression.
A ANN is characterized by two main components: a set of nodes, and the connections between nodes. The nodes can be seen as computational units that receive external information (inputs) and process it to obtain an answer (output), this processing might be very simple (such as summing the inputs), or quite complex (a node might be another network itself). The connections (weights) determine the information flow between nodes. They can be unidirectional, when the information flows only in one sense, and bidirectional, when the information flows in either sense.
The interactions of nodes through the connections lead to a global behaviour of the network that is conceived as emergent "knowledge". Inspired by biological neurons (Figure 1), nodes, or artificial neurons, collect signals through connections as the synapses located on the dendrites or membrane of the organic neuron. When the signals received are strong enough (beyond a certain threshold) the neuron is activated and sends out a signal through the axon to another synapse and might activate other neurons. The higher the connections (weights) between neurons, the stronger the influence of the nodes connected on the modelled system.
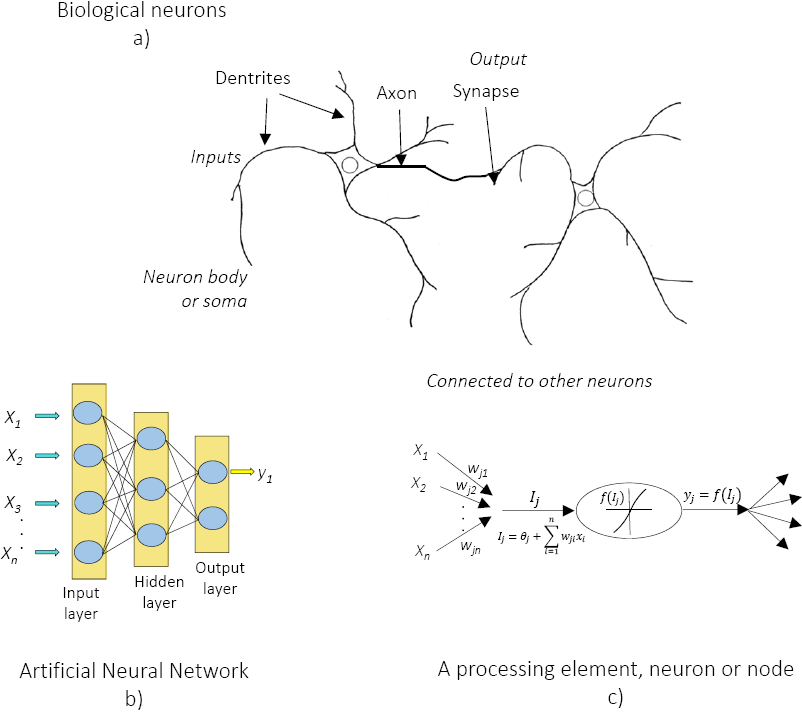
- QUOTE: Since the first neural model by McCulloch and Pitts (1943), hundreds of different models have been developed. Given that the function of ANNs is to process information, they are used mainly in fields related to this topic. The wide variety of ANNs used for engineering purposes works mainly in pattern recognition, forecasting, and data compression.
2014
- (Gomes, 2014) ⇒ Lee Gomes (2014). Machine-learning maestro michael jordan on the delusions of big data and other huge engineering efforts. IEEE Spectrum, Oct, 20.
- Michael I. Jordan: … And there, each “neuron” is really a cartoon. It’s a linear-weighted sum that’s passed through a nonlinearity. Anyone in electrical engineering would recognize those kinds of nonlinear systems.
2005
- (Golda, 2005) ⇒ Adam Gołda (2005). Introduction to neural networks. AGH-UST.
- QUOTE: The scheme of the neuron can be made on the basis of the biological cell. Such element consists of several inputs. The input signals are multiplied by the appropriate weights and then summed. The result is recalculated by an activation function.
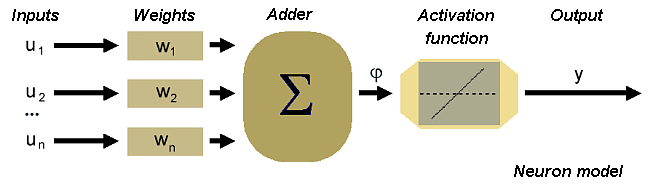
In accordance with such model, the formula of the activation potential [math]\displaystyle{ \varphi }[/math] is as follows
[math]\displaystyle{ \varphi=\sum_{i=1}^Pu_iw_i }[/math]
Signal [math]\displaystyle{ \varphi }[/math] is processed by activation function, which can take different shapes.
- QUOTE: The scheme of the neuron can be made on the basis of the biological cell. Such element consists of several inputs. The input signals are multiplied by the appropriate weights and then summed. The result is recalculated by an activation function.
2003
- (Aryal & Wang, 2003) ⇒ Aryal, D. R., & Wang, Y. W. (2003). “The Basic Artificial Neuron" In: Neural network Forecasting of the production level of Chinese construction industry. Journal of comparative international management, 6(2).
- QUOTE: The first computational neuron was developed in 1943 by the neurophysiologist Warren McCulloch and the logician Walter Pits based on the biological neuron. It uses the step function to fire when threshold [math]\displaystyle{ \mu }[/math] is exceeded. If the step activation function is used (i.e. the neuron's output is 0 if the input is less than zero, and 1 if the input is greater than or equal to 0) then the neuron acts just like the biological neuron described earlier. Artificial neural networks are comprised of many neurons, interconnected in certain ways to cast them into identifiable topologies as depicted in Figure 2.
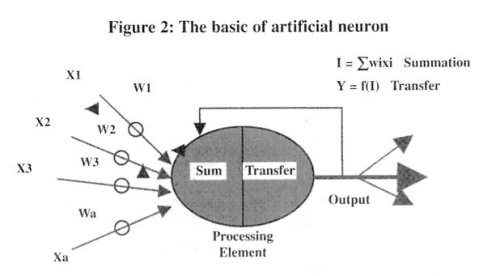
Note that various inputs to the network are represented by the mathematical symbol, [math]\displaystyle{ x(n) }[/math]. Each of these inputs is multiplied by a connection weights [math]\displaystyle{ w(n) }[/math]. In the simplest case, these products are simply summed, fed through a transfer function to generate a result, and then output. Even though all artificial neural networks are constructed from this basic building block the fundamentals vary in these building blocks and there are some differences.
- QUOTE: The first computational neuron was developed in 1943 by the neurophysiologist Warren McCulloch and the logician Walter Pits based on the biological neuron. It uses the step function to fire when threshold [math]\displaystyle{ \mu }[/math] is exceeded. If the step activation function is used (i.e. the neuron's output is 0 if the input is less than zero, and 1 if the input is greater than or equal to 0) then the neuron acts just like the biological neuron described earlier. Artificial neural networks are comprised of many neurons, interconnected in certain ways to cast them into identifiable topologies as depicted in Figure 2.
1943
- (McCulloch & Pitts, 1943) ⇒ McCulloch, W. S., & Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. The bulletin of mathematical biophysics, 5(4), 115-133.
- ABSTRACT: Because of the “all-or-none” character of nervous activity, neural events and the relations among them can be treated by means of propositional logic. It is found that the behavior of every net can be described in these terms, with the addition of more complicated logical means for nets containing circles; and that for any logical expression satisfying certain conditions, one can find a net behaving in the fashion it describes. It is shown that many particular choices among possible neurophysiological assumptions are equivalent, in the sense that for every net behaving under one assumption, there exists another net which behaves under the other and gives the same results, although perhaps not in the same time. Various applications of the calculus are discussed.