A* Shortest Path Algorithm
An A* Shortest Path Algorithm is a shortest path algorithm that is a modification of Dijkstra's Algorithm that is optimized for a single destination.
- Context:
- It can (typically) be a Dynamic Programming-based Algorithm.
- It can be implemented by an A* Shortest Path-based System.
- It uses a uniform-cost heuristic that assigns a weight to each open node equal to the weight of the edge to that node plus the approximate distance between that node and the finish.
- It finds paths to one location, or the closest of several locations while Dijkstra's Algorithm can find paths to all locations.
- Example(s):
- Counter-Example(s)
- See: Graph Search Algorithm, Pathfinding, Graph Traversal Algorithm.
References
2021
- (Patel, 2021) ⇒ Amit Patel (2021). "Introduction to A*". In: Thoughts on Pathfinding.
- QUOTE: I will be focusing on the A* Algorithm. A* is the most popular choice for pathfinding, because it’s fairly flexible and can be used in a wide range of contexts.
A* is like Dijkstra's Algorithm in that it can be used to find a shortest path. A* is like Greedy Best-First-Search in that it can use a heuristic to guide itself. In the simple case, it is as fast as Greedy Best-First-Search:

In the example with a concave obstacle, A* finds a path as good as what Dijkstra’s Algorithm found:
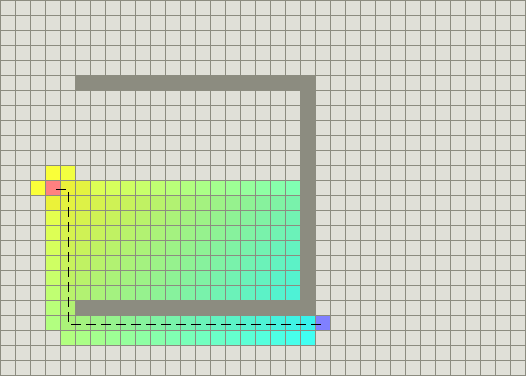
The secret to its success is that it combines the pieces of information that Dijkstra's Algorithm uses (favoring vertices that are close to the starting point) and information that Greedy Best-First-Search uses (favoring vertices that are close to the goal). In the standard terminology used when talking about A*, $g(n)$ represents the exact cost of the path from the starting point to any vertex $n$, and $h(n)$ represents the heuristic estimated cost from vertex $n$ to the goal. In the above diagrams, the yellow ($h$) represents vertices far from the goal and teal ($g$) represents vertices far from the starting point. A* balances the two as it moves from the starting point to the goal. Each time through the main loop, it examines the vertex $n$ that has the lowest $f(n) = g(n) + h(n)$.
- QUOTE: I will be focusing on the A* Algorithm. A* is the most popular choice for pathfinding, because it’s fairly flexible and can be used in a wide range of contexts.
2017
- (Wikipedia, 2017) ⇒ https://en.wikipedia.org/wiki/A*_search_algorithm Retrieved:2017-12-5.
- In computer science, A* (pronounced as "A star") is a computer algorithm that is widely used in pathfinding and graph traversal, the process of plotting an efficiently directed path between multiple points, called nodes. It enjoys widespread use due to its performance and accuracy. However, in practical travel-routing systems, it is generally outperformed by algorithms which can pre-process the graph to attain better performance, although other work has found A* to be superior to other approaches.[1] Peter Hart, Nils Nilsson and Bertram Raphael of Stanford Research Institute (now SRI International) first described the algorithm in 1968.[2] It is an extension of Edsger Dijkstra's 1959 algorithm. A* achieves better performance by using heuristics to guide its search.
- ↑ Zeng, W.; Church, R. L. (2009). "Finding shortest paths on real road networks: the case for A*". International Journal of Geographical Information Science. 23 (4): 531–543. doi:10.1080/13658810801949850. S2CID 14833639.
- ↑ Nilsson, Nils J. (2009-10-30). The Quest for Artificial Intelligence (PDF). Cambridge: Cambridge University Press. ISBN 9780521122931.
2016
- (Wikipedia, 2016) ⇒ http://en.wikipedia.org/wiki/Pathfinding#A*_algorithm
- QUOTE: A* is a variant of Dijkstra's algorithm commonly used in games. A* assigns a weight to each open node equal to the weight of the edge to that node plus the approximate distance between that node and the finish. This approximate distance is found by the heuristic, and represents a minimum possible distance between that node and the end. This allows it to eliminate longer paths once an initial path is found. If there is a path of length x between the start and finish, and the minimum distance between a node and the finish is greater than x, that node need not be examined.[1]
A* uses this heuristic to improve on the behavior relative to Dijkstra's algorithm. When the heuristic evaluates to zero, A* is equivalent to Dijkstra's algorithm. As the heuristic estimate increases and gets closer to the true distance, A* continues to find optimal paths, but runs faster (by virtue of examining fewer nodes). When the value of the heuristic is exactly the true distance, A* examines the fewest nodes. (However, it is generally impractical to write a heuristic function that always computes the true distance.) As the value of the heuristic increases, A* examines fewer nodes but no longer guarantees an optimal path. In many applications (such as video games) this is acceptable and even desirable, in order to keep the algorithm running quickly.
- QUOTE: A* is a variant of Dijkstra's algorithm commonly used in games. A* assigns a weight to each open node equal to the weight of the edge to that node plus the approximate distance between that node and the finish. This approximate distance is found by the heuristic, and represents a minimum possible distance between that node and the end. This allows it to eliminate longer paths once an initial path is found. If there is a path of length x between the start and finish, and the minimum distance between a node and the finish is greater than x, that node need not be examined.[1]
2012b
- (Wikipedia, 2012) ⇒ http://en.wikipedia.org/wiki/A*_search_algorithm
- QUOTE: In computer science, A* (pronounced "A star" (File:Speaker Icon.svg listen)) is a computer algorithm that is widely used in pathfinding and graph traversal, the process of plotting an efficiently traversable path between points, called nodes. Noted for its performance and accuracy, it enjoys widespread use. … It is an extension of Edsger Dijkstra's 1959 algorithm. A* achieves better performance (with respect to time) by using heuristics.
2009
- (Korf, 2009) ⇒ Richard E. Korf. (2009). “Artificial Intelligence Search Algorithms.” In: Algorithms and Theory of Computation Handbook. ISBN:1584888180
- QUOTE: The A* algorithm [14] combines features of uniform-cost search and pure heuristic search to efficiently compute optimal solutions. A* is a best-first search in which the cost associated with a node is f(n) = g(n) + h(n), where g(n) is the cost of the path from the initial state to node n, and h(n) is the heuristic estimate of the cost of a path from node n to a goal. At each point a node with lowest f value is chosen for expansion. Ties among nodes of equal f value are broken in favor of nodes with lower h values. The algorithm terminates when a goal node is chosen for expansion. A* finds an optimal path to a goal if the heuristic function h(n) is admissible, meaning it never overestimates actual cost. … The main drawback of A*, and indeed of any best-first search, is its memory requirement. Since the open and closed lists are stored in memory, A* is severely space-limited in practice, and will exhaust the available memory on current machines in minutes.
1968
- (Hart et al., 1968) ⇒ Peter E. Hart, Nils J. Nilsson, and Bertram Raphael. (1968). “A Formal Basis for the Heuristic Determination of Minimum Cost Paths". In: IEEE Transactions on Systems Science and Cybernetics SSC4, 4(2). doi:10.1109/TSSC.1968.300136.