Latent Dirichlet Allocation Model Family
(Redirected from Latent Dirichlet Allocation)
Jump to navigation
Jump to search
A latent Dirichlet allocation model family is a generative hierarchical probabilistic metamodel that models latent groups (e.g. latent word groups that represent latent topics) within item sets (such as a bag-of-words corpus).
- AKA: LDA, Latent Dirichlet Allocation Metamodel.
- Context:
- It can be a Bayesian Topic Model designed as a latent semantic analysis model that
- represents text documents as random mixtures over unobserved groups (latent topics characterized by a word tuples and word distribution).
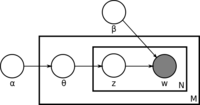
- generates each word [math]\displaystyle{ w }[/math] in document [math]\displaystyle{ d }[/math] by first sampling a topic [math]\displaystyle{ t }[/math] and then sampling a word from the Topic-Word Distribution of t.
- It can assume that the topic distribution has a Dirichlet prior.
- It can be a Constrained Latent Dirichlet Allocation Metamodel if the model includes constraints, such as Background Knowledge ((Andrzejewski et al., 2009))
- It can be trained by a Latent Dirichlet Allocation Model Training Algorithm.
- It can be used for a Topic Modeling Task.
- It can be used for a Topic Detection and Tracking Task.
- It can be a Bayesian Topic Model designed as a latent semantic analysis model that
- Example(s):
- Counter-Example(s):
- See: Probabilistic Graphical Model, Latent Semantic Analysis, Topic Modeling Algorithm.
References
2011
- (Wikipedia, 2011-Jun-22) ⇒ http://en.wikipedia.org/wiki/Latent_Dirichlet_allocation
- In statistics, latent Dirichlet allocation (LDA) is a generative model that allows sets of observations to be explained by unobserved groups that explain why some parts of the data are similar. For example, if observations are words collected into documents, it posits that each document is a mixture of a small number of topics and that each word's creation is attributable to one of the document's topics. LDA is an example of a topic model and was first presented as a graphical model for topic discovery by David Blei, Andrew Ng, and Michael Jordan in 2002. … In LDA, each document may be viewed as a mixture of various topics. This is similar to probabilistic latent semantic analysis (pLSA), except that in LDA the topic distribution is assumed to have a Dirichlet prior. In practice, this results in more reasonable mixtures of topics in a document. It has been noted, however, that the pLSA model is equivalent to the LDA model under a uniform Dirichlet prior distribution.
2008
- (Blei, 2008) ⇒ David M. Blei. (2008). “Modeling Science." Presentation. April 17, 2008
- (AlSumait et al., 2008) ⇒ Loulwah AlSumait, Daniel Barbará, and Carlotta Domeniconi. (2008). “On-line LDA: Adaptive Topic Models for Mining Text Streams with Applications to Topic Detection and Tracking.” In: Proceedings of the Eighth IEEE International Conference on Data Mining (ICDM 2008) [doi:10.1109/ICDM.2008.140].
- (Wallach, 2008) ⇒ Hanna M. Wallach. (2008). “Structured Topic Models for Language." Ph.D. Thesis, Newnham College, University of Cambridge.
2006
- (Bhattacharya & Getoor, 2006) ⇒ Indrajit Bhattacharya, and Lise Getoor. (2006). “A Latent Dirichlet Model for Unsupervised Entity Resolution.” In: Proceedings of the Sixth SIAM International Conference on Data Mining (SIAM 2006).
- (Blei & Lafferty, 2006) ⇒ David M. Blei, and John D. Lafferty. (2006). “Dynamic Topic Models.” In: Proceedings of the 23rd International Conference on Machine Learning (ICML 2006). doi:10.1145/1143844.1143859
2005
- (Steyvers & Griffiths, 2005) ⇒ Mark Steyvers, and Thomas L. Griffiths. (2005). “Probabilistic Topic Models.” In: Thomas K. Landauer (editor), D. Mcnamara (editor), S. Dennis (editor), and W. Kintsch (editor). “Latent Semantic Analysis: A Road to Meaning.” Laurence Erlbaum.
2003
- (Blei, Ng & Jordan, 2003) ⇒ David M. Blei, Andrew Y. Ng, and Michael I. Jordan. (2003). “Latent Dirichlet Allocation.” In: The Journal of Machine Learning Research, 3.
- QUOTE: We describe latent Dirichlet allocation (LDA), a generative probabilistic model for collections of discrete data such as text corpora. LDA is a three-level hierarchical Bayesian model, in which each item of a collection is modeled as a finite mixture over an underlying set of topics. … Latent Dirichlet allocation (LDA) is a generative probabilistic model of a corpus. The basic idea is that documents are represented as random mixtures over latent topics, where each topic is characterized by a distribution over words
2001
- (Blei, Ng & Jordan, 2001) ⇒ David M. Blei, Andrew Y. Ng, and Michael I. Jordan. (2001). “Latent Dirichlet Allocation.” In: Advances in Neural Information Processing Systems 14 (NIPS 2001).