Line (Geometry)

A Line (Geometry) is an one-dimensional algebraic curve of order one that only has length, without thickness or curvature.

• AKA: Line, Straight Line, Right Line.
• Context:
  • It can be mathemaically described by a two-dimensional linear equation:

    [math]\displaystyle{ ax+by+c=0 }[/math]

    or

    [math]\displaystyle{ y = mx+b_0 }[/math]

    where [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are variables; [math]\displaystyle{ m }[/math], [math]\displaystyle{ b_0 }[/math], [math]\displaystyle{ a }[/math], [math]\displaystyle{ b }[/math], [math]\displaystyle{ c }[/math] are constants. The line slope is [math]\displaystyle{ m=-a/b }[/math], y-intercept is [math]\displaystyle{ b_0=-c/b }[/math] and x-intercept is [math]\displaystyle{ c/a }[/math].

• Example(s):
  • a straight line such as [math]\displaystyle{ y = 2x+3 }[/math], with slope 2, y-intercept at 3 and x-intercept at -3/2;
  • a straight line such as [math]\displaystyle{ 2x+3y=4 }[/math], with slope -2/3, y-intercept 4/3 and x-intercept 2;
  • a vertical line such as [math]\displaystyle{ x = 1 }[/math], that crosses the x-axis at 1,
  • an horizontal line such as [math]\displaystyle{ y = 1 }[/math] that crosses the y-axis at 1,
• Counter-Example(s):
  • a Circle such as [math]\displaystyle{ x^2+y^2 = 10 }[/math] of radius [math]\displaystyle{ 10 }[/math] centred at (0,0)
  • a Parabola such [math]\displaystyle{ y=x^2+2x-8 }[/math] that opens upwards with vertex point at (-1,-9)
  • an Ellipse, such as [math]\displaystyle{ (x^2/5)+(y^2/4)=1 }[/math] with eccentricity 0.2 and focus at (0,1)
  • a Hyperbola, such as [math]\displaystyle{ x^2-y^2=1 }[/math] of length 2 and focal parameter 1.
  • a Cubic Function, such as [math]\displaystyle{ y=x^3+x^2+x+1= }[/math].
• See: Curvature, Projective Geometry, Euclidean Geometry, Conic Section, Paraboloid, Reflection Symmetry, Curve, Plane (Geometry), Point (Geometry), Focus (Geometry), Directrix (Conic Section).

---

---

References

2018a

• (Wikipedia, 2018) ⇒ https://en.wikipedia.org/wiki/Line_(geometry) Retrieved:2018-10-12.
  • The notion of line or straight line was introduced by ancient mathematicians to represent straight objects (i.e., having no curvature) with negligible width and depth. Lines are an idealization of such objects. Until the 17th century, lines were defined in this manner: "The [straight or curved] line is the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which […] will leave from its imaginary moving some vestige in length, exempt of any width. […] The straight line is that which is equally extended between its points."

     Euclid described a line as "breadthless length" which "lies equally with respect to the points on itself"; he introduced several postulates as basic unprovable properties from which he constructed all of geometry, which is now called Euclidean geometry to avoid confusion with other geometries which have been introduced since the end of the 19th century (such as non-Euclidean, projective and affine geometry).

    In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation, but in a more abstract setting, such as incidence geometry, a line may be an independent object, distinct from the set of points which lie on it.

    When a geometry is described by a set of axioms, the notion of a line is usually left undefined (a so-called primitive object). The properties of lines are then determined by the axioms which refer to them. One advantage to this approach is the flexibility it gives to users of the geometry. Thus in differential geometry a line may be interpreted as a geodesic (shortest path between points), while in some projective geometries a line is a 2-dimensional vector space (all linear combinations of two independent vectors). This flexibility also extends beyond mathematics and, for example, permits physicists to think of the path of a light ray as being a line.

2018b

• (Stover & Weisstein, 2018) ⇒ hristopher Stover, and Eric W. Weisstein (2018) "Line." From MathWorld -- A Wolfram Web Resource. http://mathworld.wolfram.com/Line.html Retrieved:2018-10-12.
  • QUOTE: A line is a straight one-dimensional figure having no thickness and extending infinitely in both directions. A line is sometimes called a straight line or, more archaically, a right line (Casey 1893), to emphasize that it has no "wiggles" anywhere along its length. While lines are intrinsically one-dimensional objects, they may be embedded in higher dimensional spaces.

     Harary (1994) called an edge of a graph a "line."

    

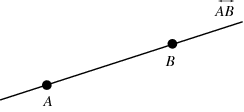
    A line is uniquely determined by two points, and the line passing through points [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] is denoted [math]\displaystyle{ \longleftrightarrow }[/math]; [math]\displaystyle{ \overleftrightarrow{AB} }[/math]. Similarly, the length of the finite line segment terminating at these points may be denoted [math]\displaystyle{ \overline{AB} }[/math]. A line may also be denoted with a single lower-case letter (Jurgensen et al. 1963, p. 22).

     Euclid defined a line as a "breadthless length," and a straight line as a line that "lies evenly with the points on itself" (Kline 1956, Dunham 1990).

    Consider first lines in a two-dimensional plane. Two lines lying in the same plane that do not intersect one another are said to be parallel lines. Two lines lying in different planes that do not intersect one another are said to be skew lines. "

    

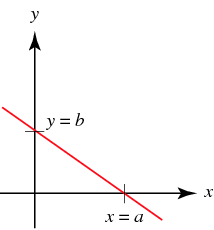
    The line with [math]\displaystyle{ x }[/math]-intercept, [math]\displaystyle{ b }[/math] and [math]\displaystyle{ y }[/math]-intercept a is given by the intercept form

    [math]\displaystyle{ \dfrac{x}{b}+\dfrac{y}{a} = 1 }[/math]

    It is not uncommon for lines in intercept form to be rewritten in what's known as standard form:

    [math]\displaystyle{ ax+by=c }[/math]

    Here, [math]\displaystyle{ c=ab }[/math].

2018c

• (Encyclopedia of Mathematics, 2018) ⇒ https://www.encyclopediaofmath.org/index.php/Straight_line Retrieved: Retrieved:2018-10-12.
  • QUOTE: One of the basic geometric concepts. A straight line is usually implicitly defined by the axioms of geometry; e.g., a Euclidean straight line by the axioms of incidence, order, congruence, and continuity. A straight line is called projective, affine, hyperbolic, etc., depending on the plane in which it is imbedded. A straight line can be studied by its transformations induced by the collineations of the plane. E.g., the group of algebraic automorphisms of a real projective straight line is isomorphic to the group of displacements of the Lobachevskii plane. Topologically, all straight lines in one plane are equivalent. Thus, the elliptic and real projective straight lines are topologically equivalent to a circle in the Euclidean plane, while the complex projective straight line is topologically equivalent to a two-dimensional sphere in the Euclidean space. A straight line is called continuous, discrete or finite if it is incident with a set of points of the cardinality of the continuum, with a countable set or with a finite set, respectively.

    In the plane over an arbitrary algebraic field, a straight line is an algebraic curve of order one. In the rectilinear coordinate system of the Euclidean plane , a straight line is given by an equation

    [math]\displaystyle{ Ax+By+C=0 }[/math]

    The coefficients (A,B) determine the coordinates of the normal vector of this straight line. …

---