Heaviside Step Function

A Heaviside Step Function is a Discontinuous Function whose value is zero for negative arguments and one for non-negative arguments.

• AKA: Unit Step Function.
• Context:
  • It is named after Oliver Heaviside.
  • …
• Example(s):
  • [math]\displaystyle{ H(x)=\begin{cases} 0,\ \text{for}\ x \lt 0 \\ \\ 1,\ \text{for}\ x\ge 0 \end{cases} }[/math]
  • [math]\displaystyle{ H(x)=\left\{\begin{array}{ll} 0 & x\lt 0 \\ \frac{1}{2} & x=0 \\ 1 & x\gt 0 \end{array}\right. }[/math]
• Counter-Example(s):
  • Ramp Function,
  • Dirac Delta Function.
• See: Continuous Function, Step Function, Linear Combination, Operational Calculus, Differential Equation.

---

---

References

2020a

• (Wikipedia, 2020) ⇒ https://en.wikipedia.org/wiki/Heaviside_step_function Retrieved:2020-10-31.
  • The Heaviside step function, or the unit step function, usually denoted by or (but sometimes , 1 or 𝟙), is a discontinuous function, named after Oliver Heaviside (1850–1925), whose value is zero for negative arguments and one for non-negative arguments. :

[math]\displaystyle{ H(x):=\begin{cases} 0,\ \text{for}\ x \lt 0 \\ \\ 1,\ \text{for}\ x\ge 0 \end{cases} }[/math]

Where at 0 the value [math]\displaystyle{ H(0)=1 }[/math] is chosen.

It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one.

The function was originally developed in operational calculus for the solution of differential equations, where it represents a signal that switches on at a specified time and stays switched on indefinitely. Oliver Heaviside, who developed the operational calculus as a tool in the analysis of telegraphic communications, represented the function as 1.

The Heaviside function may be defined as the derivative of the ramp function:

[math]\displaystyle{ H(x):= \frac{d}{dx} \max \{ x, 0 \}\quad \mbox{for } x \ne 0 }[/math]

The Dirac delta function is the derivative of the Heaviside function :

[math]\displaystyle{ \delta(x)= \frac{d}{dx} H(x) }[/math]

Hence the Heaviside function can be considered to be the integral of the Dirac delta function. This is sometimes written as :

[math]\displaystyle{ H(x) := \int_{-\infty}^x \delta(s)\,ds }[/math]

although this expansion may not hold (or even make sense) for x 0, depending on which formalism one uses to give meaning to integrals involving . In this context, the Heaviside function is the cumulative distribution function of a random variable which is almost surely 0. (See constant random variable.)

In operational calculus, useful answers seldom depend on which value is used for H(0), since is mostly used as a distribution. However, the choice may have some important consequences in functional analysis and game theory, where more general forms of continuity are considered. Some common choices can be seen below.

Approximations to the Heaviside step function are of use in biochemistry and neuroscience, where logistic approximations of step functions (such as the Hill and the Michaelis-Menten equations) may be used to approximate binary cellular switches in response to chemical signals.

The Heaviside function can also be defined, for [math]\displaystyle{ x \ne 0 }[/math] , as: :

[math]\displaystyle{ \begin{align} H(x) :&= (x + |x|) / 2x\\ H(x) :&= (1/2)(|x|/x)+ (1/2) \end{align} }[/math]

2020b

• (Mathworld, 2020) ⇒ Eric W. Weisstein (2020). “Heaviside Step Function." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/HeavisideStepFunction.html Retrieved:2020-10-31.
  • QUOTE: The Heaviside step function is a mathematical function denoted $H(x)$, or sometimes $\theta(x)$ or $u(x)$ (Abramowitz and Stegun 1972, p. 1020), and also known as the “unit step function". The term “Heaviside step function” and its symbol can represent either a piecewise constant function or a generalized function.

    {|style="border:2px solid #F4F6F6; text-align:center; vertical-align:center; border-spacing: 1px; margin: 1em auto; width: 80%"

|- | |-

|}

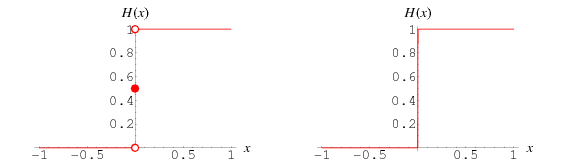
 :: When defined as a piecewise constant function, the Heaviside step function is given by

[math]\displaystyle{ H(x)=\left\{\begin{array}{ll} 0 & x\lt 0 \\ \frac{1}{2} & x=0 \\ 1 & x\gt 0 \end{array}\right. }[/math]

(1)

 :: (Abramowitz and Stegun 1972, p. 1020; Bracewell 2000, p. 61). The plot above shows this function (left figure), and how it would appear if displayed on an oscilloscope (right figure).

---