True Positive Success Rate
A True Positive Success Rate is a binary classification performance measure that is based on the Probability that a true test instance is a positive prediction.
- AKA: Recall Measure, Sensitivity, R, TPR.
- Context:
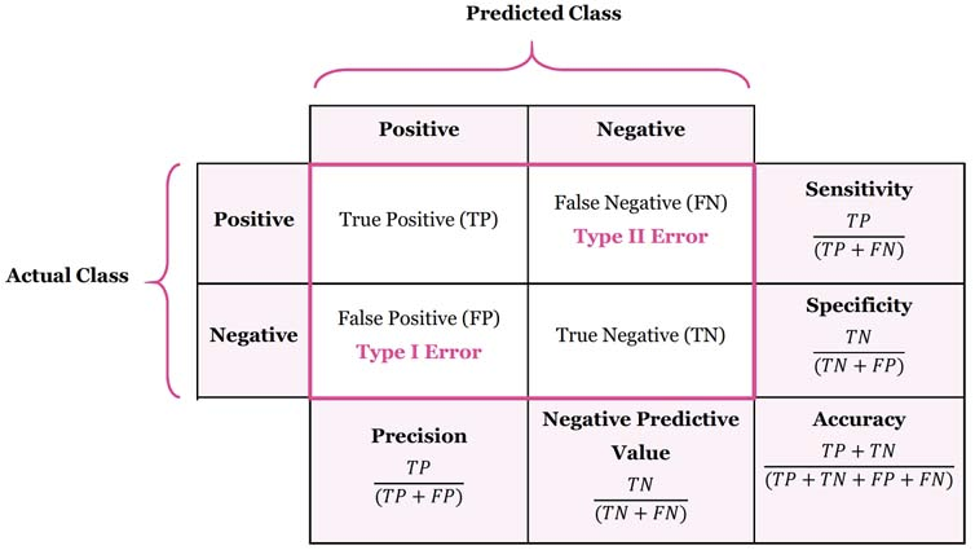
- It can be Estimated by: TP / (TP + FN)
# of correct answers given by the system as a proportion of the total # of possible correct predictions)- the proportion of cases with a positive test result who are correctly diagnosed.
- It can be illustrated over a series of cutoffs for defining an Accurate Prediction with a Receiver Operator Curve.
- It can be Estimated by: TP / (TP + FN)
- Example(s):
- The probability of a positive test result in a patient who has the disease under consideration. E.g. probability that a test for cancer will predict that a patient has cancer when in fact they do have cancer.
- a Test Sensitivity Measure.
- ...
- …
- Counter-Example(s):
- See: Receiver Operator Curve, Prevalence.
References
2021
- (Wikipedia, 2021) ⇒ https://en.wikipedia.org/wiki/Sensitivity_and_specificity Retrieved:2021-11-12.
- Sensitivity and specificity mathematically describe the accuracy of a test which reports the presence or absence of a condition, in comparison to a ‘Gold Standard’ or definition.
- Sensitivity (True Positive Rate) refers to the proportion of those who received a positive result on this test out of those who actually have the condition (when judged by the ‘Gold Standard’).
- Specificity (True Negative Rate) refers to the proportion of those who received a negative result on this test out of those who do not actually have the condition (when judged by the ‘Gold Standard’).
- In a diagnostic test, sensitivity is a measure of how well a test can identify true positives and specificity is a measure of how well a test can identify true negatives. For all testing, both diagnostic and screening, there is usually a trade-off between sensitivity and specificity, such that higher sensitivities will mean lower specificities and vice versa.
If the goal of the test is to identify everyone who has a condition, the number of false negatives should be low, which requires high sensitivity. That is, people who have the condition should be highly likely to be identified as such by the test. This is especially important when the consequence of failing to treat the condition are serious and/or the treatment is very effective and has minimal side effects.
If the goal of the test is to accurately identify people who do not have the condition, the number of false positives should be very low, which requires a high specificity. That is, people who do not have the condition should be highly likely to be excluded by the test. This is especially important when people who are identified as having a condition may be subjected to more testing, expense, stigma, anxiety, etc.
The terms "sensitivity" and "specificity" were introduced by American biostatistician Jacob Yerushalmy in 1947.

- Sensitivity and specificity mathematically describe the accuracy of a test which reports the presence or absence of a condition, in comparison to a ‘Gold Standard’ or definition.
2020
2015
- (Wikipedia, 2015) ⇒ http://en.wikipedia.org/wiki/precision_and_recall Retrieved:2015-1-20.
- In pattern recognition and information retrieval with binary classification, precision (also called positive predictive value) is the fraction of retrieved instances that are relevant, while recall (also known as sensitivity) is the fraction of relevant instances that are retrieved. Both precision and recall are therefore based on an understanding and measure of relevance. Suppose a program for recognizing dogs in scenes from a video identifies 7 dogs in a scene containing 9 dogs and some cats. If 4 of the identifications are correct, but 3 are actually cats, the program's precision is 4/7 while its recall is 4/9. When a search engine returns 30 pages only 20 of which were relevant while failing to return 40 additional relevant pages, its precision is 20/30 = 2/3 while its recall is 20/60 = 1/3.
In statistics, if the null hypothesis is that all and only the relevant items are retrieved, absence of type I and type II errors corresponds respectively to maximum precision (no false positive) and maximum recall (no false negative). The above pattern recognition example contained 7 − 4 = 3 type I errors and 9 − 4 = 5 type II errors. Precision can be seen as a measure of exactness or quality, whereas recall is a measure of completeness or quantity.
In simple terms, high precision means that an algorithm returned substantially more relevant results than irrelevant, while high recall means that an algorithm returned most of the relevant results.
- In pattern recognition and information retrieval with binary classification, precision (also called positive predictive value) is the fraction of retrieved instances that are relevant, while recall (also known as sensitivity) is the fraction of relevant instances that are retrieved. Both precision and recall are therefore based on an understanding and measure of relevance. Suppose a program for recognizing dogs in scenes from a video identifies 7 dogs in a scene containing 9 dogs and some cats. If 4 of the identifications are correct, but 3 are actually cats, the program's precision is 4/7 while its recall is 4/9. When a search engine returns 30 pages only 20 of which were relevant while failing to return 40 additional relevant pages, its precision is 20/30 = 2/3 while its recall is 20/60 = 1/3.
2011
- (Sammut & Webb, 2011) ⇒ Claude Sammut, and Geoffrey I. Webb. (2011). “Recall.” In: (Sammut & Webb, 2011) p.829
- (Sammut & Webb, 2011) ⇒ Claude Sammut, and Geoffrey I. Webb. (2011). “Sensitivity.” In: (Sammut & Webb, 2011) p.901
- (Ting, 2011d) ⇒ Kai Ming Ting. (2011). “Sensitivity and Specificity.” In: (Sammut & Webb, 2011) p.901
2009
- http://www.health.state.mn.us/newbornscreening/glossary.html#positive
- Positive predictive value - This is a measure of how well a test correctly finds individuals who truly have the condition being checked for. It is the proportion of individuals with positive test results who are correctly diagnosed.
2000
- 2000_SpeechAndLanguageProcessing.
- QUOTE: Recall is a measure of how much relevant information the system has extracted from the text; it is thus a measure of the coverage of the system.