2004 MiningFrequentPatternsWithoutCa
- (Han et al., 2004) ⇒ Jiawei Han, Jian Pei, Yiwen Yin, Runying Mao. (2004). “Mining Frequent Patterns without Candidate Generation: A Frequent-Pattern Tree Approach.” In: Journal Data Mining and Knowledge Discovery, 8(1). doi:10.1023/B:DAMI.0000005258.31418.83
Subject Headings: Frequent Pattern Mining Algorithm, Association Mining, Algorithm, Data Structure, Frequent-Pattern Tree Mining Task.
Notes
- See: Han et al. (2000).
Cited By
- Google Scholar: ~ 2,696 Citations (Retrieved 2019-10-06).
- Semantic Scholar: ~ 1,422 Citations (Retrieved 2019-10-06).
- Springer: ~ 1,167 Citations (Retrieved 2019-10-06).
Quotes
Author Keywords
Abstract
Mining frequent patterns in transaction databases, time-series databases, and many other kinds of databases has been studied popularly in data mining research. Most of the previous studies adopt an Apriori-like candidate set generation-and-test approach. However, candidate set generation is still costly, especially when there exist a large number of patterns and/or long patterns.
In this study, we propose a novel frequent-pattern tree (FP-tree) structure, which is an extended prefix-tree structure for storing compressed, crucial information about frequent patterns, and develop an efficient FP-tree-based mining method, FP-growth, for mining the complete set of frequent patterns by pattern fragment growth. Efficiency of mining is achieved with three techniques: (1) a large database is compressed into a condensed, smaller data structure, FP-tree which avoids costly, repeated database scans, (2) our FP-tree-based mining adopts a pattern-fragment growth method to avoid the costly generation of a large number of candidate sets, and (3) a partitioning-based, divide-and-conquer method is used to decompose the mining task into a set of smaller tasks for mining confined patterns in conditional databases, which dramatically reduces the search space. Our performance study shows that the FP-growth method is efficient and scalable for mining both long and short frequent patterns, and is about an order of magnitude faster than the Apriori algorithm and also faster than some recently reported new frequent-pattern mining methods.
1. Introduction
2. Frequent-Pattern Tree: Design and Construction
2.1. Frequent-Pattern Tree
(...)
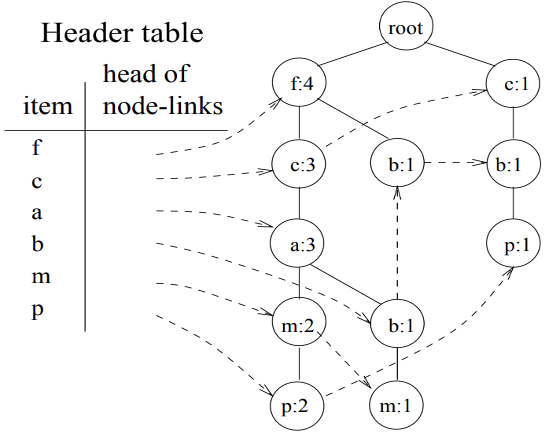
To facilitate tree traversal, an item header table is built in which each item points to its first occurrence in the tree via a node-Link. Nodes with the same item-name are linked in sequence via such node-links. After scanning all the transactions, the tree, together with the associated node-links, are shown in Figure 1.
Based on this example, a frequent-pattern tree can be designed as follows.
DEFINITION 1 (FP-tree). A frequent-pattern tree (or FP-tree in short) is a tree structure defined below.
1. It consists of one root labeled as “null”, a set of item-prefix subtrees as the children of the root, and a frequent-item-header table.
2. Each node in the item-prefix subtree consists of three fields: item-name, count, and node-link, where item-name registers which item this node represents, count registers the number of transactions represented by the portion of the path reaching this node, and node-link links to the next node in the FP-tree carrying the same item-name, or null if there is none.
3. Each entry in the frequent-item-header table consists of two fields, (1) item-name and (2) head of node-link (a pointer pointing to the first node in the FP-tree carrying the item-name).
(...)
==== 2.2. Completeness And Compactness Of FP-Tree ====
3. Mining Frequent Patterns Using FP-tree
3.1. Principles Of Frequent-Pattern Growth For FP-Tree Mining
3.2. Frequent-Pattern Growth With Single Prefix Path Of FP-Tree
3.3. The Frequent-Pattern Growth Algorithm
4. Scaling FP-Tree-Based FP-Growth by Database Projection
5. Experimental Evaluation and Performance Study
5.2. Environments Of Experiments
5.3. Compactness Of FP-Tree
5.4. Scalability Study
6. Discussions
The frequent-pattern growth method introduced here represents an interesting approach for scalable frequent-pattern mining. In this section, we discuss some additional issues related to its implementation, usage, and extension.
6.1. Materialization And Maintenance Of FP-Trees
Although we have studied the dynamic generation of FP-trees, it is possible to materialize and incrementally update an FP-tree. We examine the related issues here.
6.1.1. Construction of disk-resident FP-trees
When the database grows very large, it is unrealistic to construct a main memory—based FP-tree. Database projection has been introduced in Section 3.4 as an effective approach. An interesting alternative is to construct a disk-resident FP-tree.
The B+-tree structure, popularly used in relational database systems, can be used to index FP-tree as well. Since there are many operations localized to single paths or individual item prefix sub-trees, such as pattern matching for node insertion, creation of transformed prefix paths for each node ai, etc., it is important to cluster FP-tree nodes according to the tree/subtree structure. That is, one should (1) store each item prefix sub—tree on the same page, if possible, or at least on a sequence of continuous pages on disk; (2) store each subtree on the same page, and put the shared prefix path as the header information of the page; and (3) cluster the node—links belonging to the same paged nodes together, etc. This also facilitates a breadth—first search fashion for mining all the patterns starting from all the nodes in the header in parallel.
To reduce the I/O costs by following node—links, mining should be performed in a group accessing mode, that is, when accessing nodes following node—links, one should exhaust the node traversal tasks in main memory before fetching the nodes on disks.
Notice that one may also construct node-link-free FP—trees. In this case, when traversing a tree path, one should project the prefix subpaths of all the nodes into the corresponding conditional pattern bases. This is feasible if both FP-tree and one page of each of its one—level conditional pattern bases can fit in memory. Otherwise, additional I / Os will be needed to swap in and out the conditional pattern bases.
6.1.2. Materialization Of An FP-Tree For Frequent-Pattern Mining
Although an FP-tree is rather compact, its construction needs two scans of a transaction database, which may represent a nontrivial overhead. It could be beneficial to materialize an FP-tree for regular frequent pattern mining.
One difficulty for FP-tree materialization is how to select a good minimum support threshold 5 in materialization since 5 is usually query-dependent. To overcome this difficulty, one may use a low 5 that may usually satisfy most of the mining queries in the FP-tree construction. For example, if we notice that 98% queries have 5 Z 20, we may choose 5 = 20 as the FP-tree materialization threshold: that is, only 2% of queries may need to construct a new FP-tree. Since an FP-tree is organized in the way that less frequently occurring items are located at the deeper paths of the tree, it is easy to select only the upper portions of the FP-tree (or drop the low portions which do not satisfy the support threshold) when mining the queries with higher thresholds. Actually, one can directly work on the materialized FP-tree by starting at an appropriate header entry since one just need to get the prefix paths no matter how low support the original FP-tree is.
6.1.3. Incremental update of an FP-tree
Another issue related to FP-tree materialization is how to incrementally update an FP-tree, such as when adding daily new transactions into a database containing records accumulated for months.
If the materialized FP-tree takes 1 as its minimum support (i.e., it is just a compact version of the original database), the update will not cause any problem since adding new records is equivalent to scanning additional transactions in the FP-tree construction. However, a full FP-tree may be an undesirably large. Thus setting 1 as its minimum support may not be a good solution.
In the general case, we can register the occurrence frequency of every items in F1 and track them in updates. This is not too costly but it benefits the incremental updates of an FP-tree as follows. Suppose an FP-tree was constructed based on a validity support threshold (called “watermark”) w = 0.1% in a DB with 108 transactions. Suppose an additional 106 transactions are added in. The frequency of each item is updated. If the highest relative frequency among the originally infrequent items (i.e., not in the FP-tree) goes up to, say 12%, the watermark will need to go up accordingly to w > 0.12% to exclude such item(s). However, with more transactions added in, the watermark may even drop since an item’s relative support frequency may drop with more transactions added in. Only when the FP-tree watermark is raised to some undesirable level, the reconstruction of the FP-tree for the new DB becomes necessary.
6.2. Extensions Of Frequent-Pattern Growth Method In Data Mining
The philosophy of database compression and partition—based frequent-pattern mining can be ex- tended to constraint-based mining and mining other kinds of frequent patterns, such as max-patterns, sequential patterns.
6.2.1. FP-Tree Mining With Constraints
Constraint-based frequent-pattern mining represents an important direction towards user-controlled data mining. Constraint-based association mining using the Apriori-like mining methodology has been studied extensively (SVA97; NLHP98). With the introduction of FP—growth method, one may wonder whether constraint-based mining may benefit with FP-tree—like structures. A thorough study of this issue, such as classification of various kinds of constraints and development of methods of FP-tree- based mining with sophisticated constraints, such as those in (NLHP98), should be the task of another research paper[1]. Here we only show how to apply FP-tree structure to mining frequent patterns by incorporation of constraints associated with a set of items.
Suppose one may just like to derive frequent patterns only associated with a particular set of items, S, such as mining the set of frequent patterns containing 0 or m in Example 1. Instead of mining frequent patterns for all the frequent items, one may explore the FP-tree—based mining as follows. With the same FP-tree, the FP-growth mining method may just need to be modified minorly. The only additional care is when computing a transformed prefix path for an item m, one also needs to look down the path to include the items, such as p, which are not in S. Our previous computation for the whole database will not need to consider m’s pairing with p since it would have been checked when examining node p. However, since p is not in S now, such a pair would have been missed if m’s computation did not look down the path to include p.
6.2.2. FP—Tree Mining Of Other Frequent Patterns
FP-tree—based mining method can be extended to mining many other kinds of interesting frequent patterns. We examine a few such examples.
The first example is on mining frequent closed itemsets. Since frequent pattern mining often generates a very large number of frequent itemsets, it hinders the effectiveness of mining since users have to sift through a large number of mined rules to find useful ones. An interesting alternative method proposed recently by Pasquier et a1. (PBTL99) is to mine frequent closed itemsets, where an itemset a is a closed itemset if there exists no proper superset of a that has the same support as a in the database. Mining frequent closed itemsets has the same power as mining the complete set of frequent itemsets, but it may substantially reduce redundant rules to be generated and increase the effectiveness of mining. A study at mining closed items using an Apriori-like philosophy but adopting a vertical data format, i.e., viewing database as “(item_id: a set of transactions)” instead of “(transaction_id: a set of items),” has been studied in (ZH02). The FP-tree—based frequent-pattern growth method can be extended and further optimized for mining such closed itemsets, which has been reported in our subsequent study, as a new closed pattern mining algorithm, called CLOSET (PHM00).
The second example is on mining sequential patterns. A sequential patterns is a frequent pattern in an event sequence database where a sequence is a set of events happening at different times. Most of the previously developed sequential pattern mining methods, such as (AS95; SA96; MTV97), follow the methodology of Apriori since the Apriori-based method may substantially reduce the number of combinations to be examined. However, Apriori still encounters problems when a sequence database is large and/ or when sequential patterns to be mined are numerous and / or long. Our frequent-pattern growth method can be extended to mining sequential patterns using the ideas of projection of sequence database and growth of subsequence fragments to confine search space. An efficient sequential pattern method, called PrefixSpan (PHMA+01), has been developed in this direction and our performance study has shown a substantial performance improvement over the Apriori—based GSP algorithm (SA96).
7. Conclusions
We have proposed a novel data structure, frequent pattern tree (FP-tree), for storing compressed, crucial information about frequent patterns, and developed a pattern growth method, FP—growth, for efficient mining of frequent patterns in large databases.
There are several advantages of FP—growth over other approaches: (1) It constructs a highly compact FP-tree, which is usually substantially smaller than the original database and thus saves the costly database scans in the subsequent mining processes. (2) It applies a pattern growth method which avoids costly candidate generation and test by successively concatenating frequent 1-itemset found in the (conditional) FP-trees. This ensures that it never generates any combinations of new candidate sets which are not in the database because the itemset in any transaction is always encoded in the corresponding path of the FP-trees. In this context, mining is not Apriori-like (restricted) generation- and—test but frequent pattern (fragment) growth only. The major operations of mining are count accumulation and prefix path count adjustment, which are usually much less costly than candidate generation and pattern matching operations performed in most Apriori-like algorithms. (3) It applies a partitioning-based divide—and-conquer method which dramatically reduces the size of the subsequent conditional pattern bases and conditional FP-tree. Several other optimization techniques, including direct pattern generation for single tree-path and employing the least frequent events as suffix, also contribute to the efficiency of the method.
We have implemented the FP—growth method, studied its performance in comparison with several influential frequent pattern mining algorithms in large databases. Our performance study shows that the method mines both short and long patterns efficiently in large databases, outperforming the current candidate pattern generation-based algorithms. The FP-growth method has also been implemented in the DBMiner system and been tested in large industrial databases, such as a retail chain database, with satisfactory performance.
Since our first publication of FP—growth method for mining frequent patterns without candidate generation (HPY00), there have been many subsequent studies on improvements of performance of frequent patterns based on the pattern-growth philosophy, as well as extension of the scope of the method to cover other kinds of pattern mining tasks. The pattern-growth framework has been extended towards (1) mining closed itemsets as proposed in the CLOSET algorithm (PHM00), (2) mining sequential patterns as proposed in the PrefixSpan algorithm (PHMA+01), and (3) pushing tough constraints deep into frequent pattern mining processes (PHL01a). Moreover, a notable effort is the proposal of the H-mine algorithm (PHL+01b) for mining frequent patterns efficiently in sparse data sets. FP—growth, though efficient at mining dense data sets, may incur unnecessary overhead due to its recursive construction of FP-trees. Following the philosophy of frequent pattern growth, but not constructing FP-trees, the H-mine algorithm constructs another data structure, called H—struct, and mines directly on the H-struct without recursive generation of numerous conditional FP-trees. The ex- periments reported in (PHL+01b) shows that H-mine outperforms FP—growth when database is sparse. A suggested approach is to integrate the two algorithms and dynamically select the FP-tree—based and H-struct-based algorithms based on the characteristics of current data distribution.
There are still many interesting research issues related to the extensions of pattern-growth approach, such as mining structured patterns by further development of the frequent pattern-growth approach, mining approximate or fault-tolerant patterns in noisy environments, frequent-pattern—based clustering and classification, and so on.
Acknowledgements. We would like to express our thanks to anonymous reviewers of our conference and journal submissions on this theme. Their constructive comments have improved the quality of this work.
Footnotes
- ↑ One such study has been performed by us in (PHLOla).
References
- Agarwal, R., Aggarwal, C., and Prasad, V.V.V. 2001. A tree projection algorithm for generation of frequent itemsets. Journal of Parallel and Distributed Computing, 61:350–371
- Agrawal, R., Imielinski, T., and Swami, A. 1993. Mining association rules between sets of items in large databases. In Proc. 1993 ACM-SIGMOD Int. Conf. Management of Data (SIGMOD'93), Washington, DC, pp. 207–216.
- Agrawal, R., Mannila, H., Srikant, R., Toivonen, H., and Verkamo, A.I. 1996. Fast discovery of association rules. In Advances in Knowledge Discovery and Data Mining, U.M. Fayyad, G. Piatetsky-Shapiro, P. Smyth, and R. Uthurusamy (Eds.), AAAI/MIT Press, pp. 307–328.
- Agrawal, R. and Srikant, R. 1994. Fast algorithms for mining association rules. In Proc. 1994 Int. Conf. Very Large Data Bases (VLDB'94), Santiago, Chile, pp. 487–499.
- Agrawal, R. and Srikant, R. 1995. Mining sequential patterns. In Proc. 1995 Int. Conf. Data Engineering (ICDE'95), Taipei, Taiwan, pp. 3–14.
- Bayardo, R.J. 1998. Efficiently mining long patterns from databases. In Proc. 1998 ACM-SIGMOD Int. Conf. Management of Data (SIGMOD'98), Seattle, WA, pp. 85–93.
- Brin, S., Motwani, R., and Silverstein, C. 1997. Beyond market basket: Generalizing association rules to correlations. In Proc. 1997 ACM-SIGMOD Int. Conf. Management of Data (SIGMOD'97), Tucson, Arizona, pp. 265–276.
- Dong, G. and Li, J. 1999. Efficient mining of emerging patterns: Discovering trends and differences. In Proc. 1999 Int. Conf. Knowledge Discovery and Data Mining (KDD'99), San Diego, CA, pp. 43–52.
- Grahne, G., Lakshmanan, L., and Wang, X. 2000. Efficient mining of constrained correlated sets. In Proc. 2000 Int. Conf. Data Engineering (ICDE'00), San Diego, CA, pp. 512–521.
- Han, J., Dong, G., and Yin, Y. 1999. Efficient mining of partial periodic patterns in time series database. In Proc. 1999 Int. Conf. Data Engineering (ICDE'99), Sydney, Australia, pp. 106–115.
- Han, J., Pei, J., and Yin, Y. 2000. Mining frequent patterns without candidate generation. In Proc. 2000 ACMSIGMOD Int. Conf. Management of Data (SIGMOD'00), Dallas, TX, pp. 1–12.
- Kamber, M., Han, J., and Chiang, J.Y. 1997. Metarule-guided mining of multi-dimensional association rules using data cubes. In Proc. 1997 Int. Conf. Knowledge Discovery and Data Mining (KDD'97), Newport Beach, CA, pp. 207–210.
- Lent, B., Swami, A., and Widom, J. 1997. Clustering association rules. In Proc. 1997 Int. Conf. Data Engineering (ICDE'97), Birmingham, England, pp. 220–231.
- Mannila, H., Toivonen, H., and Verkamo, A.I. 1994. Efficient algorithms for discovering association rules. In Proc. AAAI'94 Workshop Knowledge Discovery in Databases (KDD'94), Seattle, WA, pp. 181–192.
- Mannila, H., Toivonen, H., and Verkamo, A.I. 1997. Discovery of frequent episodes in event sequences. Data Mining and Knowledge Discovery, 1:259–289.
- Ng, R., Lakshmanan, L.V.S., Han, J., and Pang, A. 1998. Exploratory mining and pruning optimizations of constrained associations rules. In Proc. 1998 ACM-SIGMOD Int. Conf. Management of Data (SIGMOD'98), Seattle, WA, pp. 13–24.
- Pasquier, N., Bastide, Y., Taouil, R., and Lakhal, L. 1999. Discovering frequent closed itemsets for association rules. In Proc. 7th Int. Conf. Database Theory (ICDT'99), Jerusalem, Israel, pp. 398–416.
- Park, J.S., Chen, M.S., and Yu, P.S. 1995. An effective hash-based algorithm for mining association rules. In Proc. 1995 ACM-SIGMOD Int. Conf. Management of Data (SIGMOD'95), San Jose, CA, pp. 175–186.
- Pei, J., Han, J., and Lakshmanan, L.V.S. 2001. Mining frequent itemsets with convertible constraints. In Proc. 2001 Int. Conf. Data Engineering (ICDE'01), Heidelberg, Germany, pp. 433–332.
- Pei, J., Han, J., Lu, H., Nishio, S., Tang, S., and Yang, D. 2001. H-Mine: Hyper-structure mining of frequent patterns in large databases. In Proc. 2001 Int. Conf. Data Mining (ICDM'01), San Jose, CA, pp. 441–448.
- Pei, J., Han, J., and Mao, R. 2000. CLOSET: An efficient algorithm for mining frequent closed itemsets. In Proc. 2000 ACM-SIGMOD Int. Workshop Data Mining and Knowledge Discovery (DMKD'00), Dallas, TX, pp. 11–20.
- Pei, J., Han, J., Mortazavi-Asl, B., Pinto, H., Chen, Q., Dayal, U., and Hsu, M.-C. 2001. PrefixSpan: Mining sequential patterns efficiently by prefix-projected pattern growth. In Proc. 2001 Int. Conf. Data Engineering (ICDE'01), Heidelberg, Germany, pp. 215–224.
- Srikant, R. and Agrawal, R. 1996. Mining sequential patterns: Generalizations and performance improvements. In Proc. 5th Int. Conf. Extending Database Technology (EDBT'96), Avignon, France, pp. 3–17.
- Silverstein, C., Brin, S., Motwani, R., and Ullman, J. 1998. Scalable techniques for mining causal structures. In Proc. 1998 Int. Conf. Very Large Data Bases (VLDB'98), New York, NY, pp. 594–605.
- Savasere, A., Omiecinski, E., and Navathe, S. 1995. An efficient algorithm for mining association rules in large databases. In Proc. 1995 Int. Conf. Very Large Data Bases (VLDB'95), Zurich, Switzerland, pp. 432–443.
- Sarawagi, S., Thomas, S., and Agrawal, R. 1998. Integrating association rule mining with relational database systems: Alternatives and implications. In Proc. 1998 ACM-SIGMOD Int. Conf. Management of Data (SIGMOD '98), Seattle, WA, pp. 343–354.
- Srikant, R., Vu, Q., and Agrawal, R. 1997. Mining association rules with item constraints. In Proc. 1997 Int. Conf. Knowledge Discovery and Data Mining (KDD'97), Newport Beach, CA, pp. 67–73.
- Zaki, M.J. and Hsiao, C.J. 2002. CHARM: An efficient algorithm for closed itemset mining. In Proc. 2002 SIAM Int. Conf. Data Mining, Arlington, VA, pp. 457–473.
,
| Author | volume | Date Value | title | type | journal | titleUrl | doi | note | year | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2004 MiningFrequentPatternsWithoutCa | Jian Pei Yiwen Yin Runying Mao Jiawei Han | Mining Frequent Patterns without Candidate Generation: A Frequent-Pattern Tree Approach | http://www.cs.uiuc.edu/homes/hanj/pdf/dami04 fptree.pdf | 10.1023/B:DAMI.0000005258.31418.83 |