Adaptive Piecewise Linear Activation Function
An Adaptive Piecewise Linear (APL) Activation Function is a neuron activation function that is based on the piecewise linear function: [math]\displaystyle{ f(x) = \max(0,x) + \sum_{s=1}^{S}a_i^s \max(0, -x + b_i^s) }[/math] [math]\displaystyle{ }[/math].
- AKA: APL.
- Context:
- It can (typically) be used in the activation of Adaptive Piecewise Linear Neurons.
- Example(s):
- …
- Counter-Example(s):
- a Softmax-based Activation Function,
- a Rectified-based Activation Function,
- a Heaviside Step Activation Function,
- a Ramp Function-based Activation Function,
- a Logistic Sigmoid-based Activation Function,
- a Hyperbolic Tangent-based Activation Function,
- a Gaussian-based Activation Function,
- a Softsign Activation Function,
- a Softshrink Activation Function,
- a Bent Identity Activation Function,
- a Maxout Activation Function.
- See: Artificial Neural Network, Artificial Neuron, Neural Network Topology, Neural Network Layer, Neural Network Learning Rate.
References
2017
- (Mate Labs, 2017) ⇒ Mate Labs Aug 23, 2017. Secret Sauce behind the beauty of Deep Learning: Beginners guide to Activation Functions
- QUOTE: Adaptive Piecewise Linear (APL)
Range: [math]\displaystyle{ (-\infty,+\infty) }[/math]
[math]\displaystyle{ f(x) = \max(0,x) + \sum_{s=1}^{S}a_i^s \max(0, -x + b_i^s) }[/math]
- QUOTE: Adaptive Piecewise Linear (APL)
2014
- (Agostinelli et al., 2014) ⇒ Agostinelli, F., Hoffman, M., Sadowski, P., & Baldi, P. (2014). "Learning activation functions to improve deep neural networks". arXiv preprint arXiv:1412.6830.
- QUOTE: Here we define the adaptive piecewise linear (APL) activation unit. Our method formulates the activation function [math]\displaystyle{ h_i(x) }[/math] of an APL unit i as a sum of hinge-shaped functions,
[math]\displaystyle{ h_i(x) = \max(0,x) + \sum_{s=1}^{S}a_i^s \max(0, -x + b_i^s) (1) }[/math]
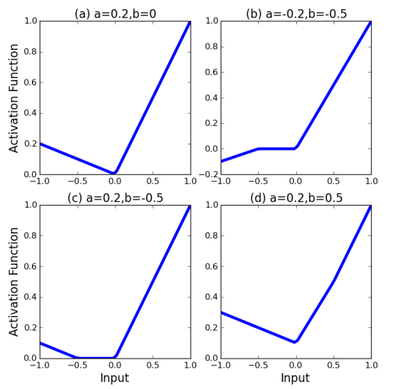
The result is a piecewise linear activation function. The number of hinges, [math]\displaystyle{ S }[/math], is a hyperparameter set in advance, while the variables [math]\displaystyle{ a^s_i , b^s_i }[/math] for [math]\displaystyle{ i \in 1,\cdots, S }[/math] are learned using standard gradient descent during training. The [math]\displaystyle{ a^s_i }[/math] variables control the slopes of the linear segments, while the [math]\displaystyle{ b^s_i }[/math] variables determine the locations of the hinges. The number of additional parameters that must be learned when using these APL units is [math]\displaystyle{ 2SM }[/math], where [math]\displaystyle{ M }[/math] is the total number of hidden units in the network. This number is small compared to the total number of weights in typical networks. Figure 1 shows example APL functions for [math]\displaystyle{ S = 1 }[/math]. Note that unlike maxout, the class of functions that can be learned by a single unit includes non-convex functions.
Figure 1: Sample activation functions obtained from changing the parameters. Notice that figure b shows that the activation function can also be non-convex. Asymptotically, the activation functions tend to [math]\displaystyle{ g(x) = x }[/math] as [math]\displaystyle{ x \rightarrow \infty }[/math] and [math]\displaystyle{ g(x) = \alpha x − c }[/math] as x ← −∞ for some α and c. S = 1 for all plots.
- QUOTE: Here we define the adaptive piecewise linear (APL) activation unit. Our method formulates the activation function [math]\displaystyle{ h_i(x) }[/math] of an APL unit i as a sum of hinge-shaped functions,