Exponential Probability Distribution Family
Am Exponential Probability Distribution Family is a probability distribution family that is restricted to exponential functions (composed of exponential probability functions).
- Context:
- It can (typically) represent (be instantiated by) on or more Exponential Probability Functions.
- …
- Example(s):
- Counter-Example(s):
- See: Central Limit Theorem, Linear Probability Models.
References
2021
- https://mariushobbhahn.com/2021-06-10-ExpFam_tutorial/
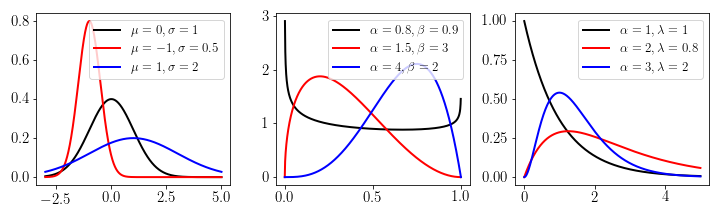
- QUOTE: Many distributions can be written as exponential families (see e.g. Wikipedia). Some of the most prominent ones are the Normal, Beta, and Gamma distribution which are displayed for three sets of parameters respectively.
2013
- http://en.wikipedia.org/wiki/Exponential_family
- In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural distributions to consider. The concept of exponential families is credited to[1] E. J. G. Pitman,[2] G. Darmois,[3] and B. O. Koopman[4] in 1935–36. The term exponential class is sometimes used in place of "exponential family".[5]
The exponential families include many of the most common distributions, including the normal, exponential, gamma, chi-squared, beta, Dirichlet, Bernoulli, categorical, Poisson, Wishart, Inverse Wishart and many others. A number of common distributions are exponential families only when certain parameters are considered fixed and known, e.g. binomial (with fixed number of trials), multinomial (with fixed number of trials), and negative binomial (with fixed number of failures). Examples of common distributions that are not exponential families are Student's t, most mixture distributions, and even the family of uniform distributions with unknown bounds. See the section below on examples for more discussion.
Consideration of exponential-family distributions provides a general framework for selecting a possible alternative parameterisation of the distribution, in terms of natural parameters, and for defining useful sample statistics, called the natural sufficient statistics of the family. See below for more information.
- In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural distributions to consider. The concept of exponential families is credited to[1] E. J. G. Pitman,[2] G. Darmois,[3] and B. O. Koopman[4] in 1935–36. The term exponential class is sometimes used in place of "exponential family".[5]
- ↑ Andersen, Erling (September 1970). "Sufficiency and Exponential Families for Discrete Sample Spaces". Journal of the American Statistical Association (Journal of the American Statistical Association, Vol. 65, No. 331) 65 (331): 1248–1255. doi:10.2307/2284291. JSTOR 2284291. MR268992.
- ↑ Pitman, E.; Wishart, J. (1936). "Sufficient statistics and intrinsic accuracy". Mathematical Proceedings of the Cambridge Philosophical Society 32 (4): 567–579. doi:10.1017/S0305004100019307.
- ↑ Darmois, G. (1935). "Sur les lois de probabilites a estimation exhaustive" (in French). C.R. Acad. Sci. Paris 200: 1265–1266.
- ↑ Koopman, B (1936). "On distribution admitting a sufficient statistic". Transactions of the American Mathematical Society (Transactions of the American Mathematical Society, Vol. 39, No. 3) 39 (3): 399–409. doi:10.2307/1989758. JSTOR 1989758. MR1501854.
- ↑ Kupperman, M. (1958) "Probabilities of Hypotheses and Information-Statistics in Sampling from Exponential-Class Populations", Annals of Mathematical Statistics, 9 (2), 571–575 Template:JSTOR
2000
- http://turing.une.edu.au/~stat354/notes/node57.html
- QUOTE: The exponential family of distributions is a one-parameter family that can be written in the form [math]\displaystyle{ f(x;\theta)=B(\theta)h(x)e^{[p(\theta)K(x)]}, \, a\lt x \lt b, \text{ (7.3)} }[/math] where [math]\displaystyle{ \gamma\lt \theta\lt \delta }[/math]. If, in addition,
- (a) neither [math]\displaystyle{ a }[/math] nor [math]\displaystyle{ b }[/math] depends on [math]\displaystyle{ \theta }[/math],
- (b) [math]\displaystyle{ p(\theta) }[/math] is a non-trivial continuous function of [math]\displaystyle{ \theta }[/math],
- (c) each of [math]\displaystyle{ K'(x) \not\equiv 0 }[/math] and [math]\displaystyle{ h(x) }[/math] is a continuous function of [math]\displaystyle{ x }[/math], [math]\displaystyle{ a\lt x\lt b }[/math],
- we say that we have a regular case of the exponential family.
Most of the well-known distributions can be put into this form, for example, binomial, Poisson, geometric, gamma and normal
- QUOTE: The exponential family of distributions is a one-parameter family that can be written in the form [math]\displaystyle{ f(x;\theta)=B(\theta)h(x)e^{[p(\theta)K(x)]}, \, a\lt x \lt b, \text{ (7.3)} }[/math] where [math]\displaystyle{ \gamma\lt \theta\lt \delta }[/math]. If, in addition,