Statistical Hypothesis Testing Task
A Statistical Hypothesis Testing Task is a statistical inference task that evaluates competing statistical hypotheses about population parameters using sample data to make decisions under statistical uncertainty.
- AKA: Hypothesis Test, Statistical Test, Significance Test, Confirmatory Data Analysis, Hypothesis Evaluation Task, Statistical Significance Test, Null Hypothesis Testing Task, Statistical Hypothesis Test, Hypothesis Testing, Test of Significance.
- Context:
- Task Input:
- Data Requirements:
- Sample data: {(x₁,y₁,...), (x₂,y₂,...), ..., (xₙ,yₙ,...)}, drawn from univariate, bivariate, or multivariate distributions.
- Data types: Parametric tests require ratio or interval data, while non-parametric tests handle ordinal or nominal data.
- Sample relationships: Independent samples, paired samples, or repeated measures.
- Parameter Requirements:
- α (significance level): Probability threshold for Type I error, typically 0.05, 0.01, or 0.001.
- θ (population parameters): Hypothesized values for means, variances, proportions, etc.
- n (sample size): Number of observations affecting statistical power.
- δ (effect size): Minimum detectable difference for power analysis.
- Data Requirements:
- Task Output:
- Test statistic value computed from sample data.
- P-value or critical value for decision making.
- Rejection decision: Reject or fail to reject null hypothesis.
- Confidence interval for parameter estimates (optional).
- Effect size measure for practical significance (optional).
- Statistical power estimate (optional).
- Task Requirements:
- Null hypothesis (H₀) and alternative hypothesis (H₁) must be mutually exclusive and exhaustive.
- Test statistic with known sampling distribution under H₀.
- Decision rule based on significance level and test statistic distribution.
- Test assumptions must be verified (e.g., normality, independence, homoscedasticity).
- It can typically follow the hypothesis testing procedure: formulate hypotheses → select test → check assumptions → calculate statistic → make decision.
- It can typically control Type I error rate at the specified significance level.
- It can typically have statistical power determined by sample size, effect size, and significance level.
- It can typically produce Binary Decisions about statistical significance at predetermined alpha levels.
- It can typically require Random Sampling from target populations for valid inference.
- It can often require multiple testing correction when conducting several tests simultaneously.
- It can often be complemented by Effect Size Estimation and confidence intervals.
- It can often be preceded by power analysis for sample size determination.
- It can often incorporate Covariate Adjustments through regression-based tests or ANCOVA.
- It can often be misinterpreted as providing Probability of Hypothesis Truth rather than probability of data given hypothesis.
- It can range from being a Parametric Statistical Test to being a Non-Parametric Statistical Test, depending on its distributional assumptions.
- It can range from being a One-Sample Test to being a Multiple-Sample Test, depending on its group count.
- It can range from being a One-Tailed Test to being a Two-Tailed Test, depending on its directional hypothesis.
- It can range from being a Univariate Hypothesis Test to being a Multivariate Hypothesis Test, depending on its variable count.
- It can range from being a Fixed-Sample Test to being a Sequential Test, depending on its sampling plan.
- It can range from being an Exact Test to being an Asymptotic Test, depending on its distribution approximation.
- It can integrate with Statistical Software Systems for automated computation.
- It can integrate with Clinical Trial Design for treatment efficacy evaluation.
- It can integrate with Quality Control Systems for process monitoring.
- It can integrate with A/B Testing Platforms for conversion rate optimization.
- ...
- Task Input:
- Example(s):
- Location Tests for central tendency:
- Mean Tests:
- One-Sample t-Test: Testing if population mean equals specified value.
- Independent Two-Sample t-Test: Comparing means of two independent groups.
- Paired t-Test: Comparing means of paired observations.
- Welch's t-Test: Two-sample test for unequal variances.
- MANOVA: Testing multivariate mean vectors across groups.
- Median Tests:
- Wilcoxon Signed-Rank Test: Non-parametric one-sample/paired test.
- Mann-Whitney U Test: Non-parametric two-sample comparison.
- Sign Test: Simple non-parametric test for medians.
- Mood's Median Test: Testing equality of medians across groups.
- Mean Tests:
- Variance Tests for dispersion:
- Single Variance Tests:
- Chi-Square Test for Variance: Testing single population variance.
- Multiple Variance Tests:
- F-Test: Comparing two population variances.
- Levene's Test: Testing homogeneity of variances.
- Bartlett's Test: Testing equal variances across groups.
- Brown-Forsythe Test: Robust test for variance equality.
- Cochran's C Test: Testing equality of variances in blocked designs.
- Hartley's Test: Testing maximum to minimum variance ratio.
- Single Variance Tests:
- Distribution Tests for shape:
- Goodness-of-Fit Tests:
- Chi-Square Goodness-of-Fit Test: Testing categorical distributions.
- Kolmogorov-Smirnov Test: Testing continuous distributions.
- Anderson-Darling Test: Emphasizing distribution tails.
- Shapiro-Wilk Test: Testing normality.
- Lilliefors Test: Testing normality with estimated parameters.
- Cramer-von Mises Test: Testing distributional fit.
- Jarque-Bera Test: Testing normality using skewness and kurtosis.
- Independence Tests:
- Chi-Square Test of Independence: Testing categorical association.
- Fisher's Exact Test: Small-sample categorical test.
- McNemar's Test: Testing paired nominal data.
- Cochran's Q Test: Testing differences in matched samples.
- G-Test: Likelihood ratio test for independence.
- Goodness-of-Fit Tests:
- Correlation Tests for relationships:
- Pearson Correlation Test: Testing linear correlation.
- Spearman Rank Correlation Test: Testing monotonic relationship.
- Kendall's Tau Test: Testing ordinal association.
- Point-Biserial Correlation Test: Testing correlation with binary variable.
- Partial Correlation Test: Testing correlation controlling for other variables.
- ANOVA Tests for multiple groups:
- One-Way ANOVA: Comparing means across groups.
- Two-Way ANOVA: Testing main effects and interactions.
- Repeated Measures ANOVA: Within-subjects comparisons.
- Mixed ANOVA: Between and within-subjects factors.
- ANCOVA: Analysis of covariance with continuous covariates.
- MANOVA: Multivariate analysis of variance.
- Kruskal-Wallis Test: Non-parametric ANOVA.
- Friedman Test: Non-parametric repeated measures.
- Scheffe's Test: Post-hoc multiple comparisons.
- Tukey's HSD Test: Post-hoc pairwise comparisons.
- Dunnett's Test: Comparing treatments to control.
- Duncan's New Multiple Range Test: Sequential range test.
- Regression Tests for models:
- F-Test for Overall Significance: Testing model validity.
- t-Test for Coefficients: Testing individual predictors.
- Likelihood Ratio Test: Comparing nested models.
- Wald Test: Testing linear restrictions on parameters.
- Score Test: Testing parameter constraints.
- Durbin-Watson Test: Testing autocorrelation in residuals.
- Breusch-Pagan Test: Testing heteroscedasticity.
- White Test: Testing heteroscedasticity without specific form.
- Chow Test: Testing structural breaks.
- Hausman Test: Testing endogeneity.
- Sargan Test: Testing overidentifying restrictions.
- Time Series Tests:
- Augmented Dickey-Fuller Test: Testing unit roots.
- Phillips-Perron Test: Testing stationarity.
- KPSS Test: Testing trend stationarity.
- Ljung-Box Test: Testing autocorrelation.
- Portmanteau Test: Testing white noise.
- Breusch-Godfrey Test: Testing serial correlation.
- Box-Pierce Test: Testing independence in time series.
- Johansen Test: Testing cointegration.
- Sequential Tests:
- Wald's Sequential Probability Ratio Test (SPRT): Continuous monitoring.
- Group-Sequential Design: Interim analysis in clinical trials.
- Adaptive Design Test: Sample size re-estimation.
- Alpha Spending Function: Controlling Type I error in sequential tests.
- Non-Inferiority Tests:
- Non-Inferiority Trial Test: Testing treatment is not worse by margin.
- Equivalence Test: Testing treatments are similar within bounds.
- Bioequivalence Test: Testing pharmaceutical equivalence.
- Survival Analysis Tests:
- Log-Rank Test: Comparing survival curves.
- Cox Proportional Hazards Test: Testing covariate effects on survival.
- Gehan-Breslow Test: Weighted comparison of survival curves.
- Historical Examples:
- Student's t-Test (1908): William Sealy Gosset's test for small samples.
- Fisher's Exact Test (1922): R.A. Fisher's test for contingency tables.
- Neyman-Pearson Test (1933): Formalization of hypothesis testing framework by Jerzy Neyman and Egon Pearson.
- Kolmogorov-Smirnov Test (1933): Andrey Kolmogorov and Nikolai Smirnov's distribution test.
- ...
- Location Tests for central tendency:
- Counter-Example(s):
- Exploratory Data Analysis, which discovers patterns without formal hypotheses.
- Descriptive Statistics, which summarizes data without inference.
- Parameter Estimation, which estimates values rather than testing hypotheses.
- Predictive Modeling, which forecasts outcomes rather than testing claims.
- Bayesian Inference, which updates beliefs rather than binary decisions.
- Machine Learning Cross-Validation, which assesses predictive performance rather than statistical significance.
- Bootstrap Confidence Interval, which estimates parameter ranges without hypothesis tests.
- Data Mining, which discovers patterns without pre-specified hypotheses.
- See: Statistical Hypothesis, Null Hypothesis, Alternative Hypothesis, Type I Error, Type II Error, Statistical Power, P-Value, Test Statistic, Significance Level, Multiple Testing Problem, Effect Size, Confidence Interval, Neyman-Pearson Framework, Fisher's Significance Testing, Family-Wise Error Rate, False Discovery Rate, Bonferroni Correction, Power Analysis, Sample Size Calculation, Statistical Significance, Practical Significance.
References
2025-08-29
- Deep Research https://chatgpt.com/s/dr_68b1f34a2dac8191a556cdf0f75bef67
- Question: What is a Statistical Hypothesis Testing Task?
- Answer: A Statistical Hypothesis Testing Task is a confirmatory data analysis procedure (also called a hypothesis test or significance test) used in statistical inference to decide between two competing hypotheses about a population parameter, based on sample data.
- Core Components:
- Null Hypothesis (H₀): The baseline assumption representing no effect or no difference.
- Alternative Hypothesis (H₁ or Hₐ): The claim or effect of interest.
- Goal: To use sample evidence to determine whether there is sufficient statistical evidence to reject H₀ in favor of H₁, or instead fail to reject H₀.
- Decision Conditions: The decision is made under conditions of uncertainty and controlled risk of error, following a formal procedure.
- Context and Inputs:
- Data Distributions: Tests apply to data drawn from one or more populations, which may be univariate, bivariate, or multivariate distributions.
- Sample Data: Typically denoted as a set of observations ${(x_1, y_1, ...), (x_2, y_2, ...), ..., (x_n, y_n, ...)}$ collected from the population(s) of interest.
- Sample Designs:
- Independent Samples: From distinct groups or conditions.
- Paired Samples: Naturally matched or the same subjects measured twice.
- Repeated Measures: On the same subjects.
- Data Types:
- Parametric Tests: Generally require quantitative data at interval or ratio scale, often assuming normal distribution.
- Non-Parametric Tests: Can handle ordinal or nominal data without strict distributional assumptions.
- Input Parameters:
- Significance Level (α): The tolerated Type I error probability, commonly 0.05, 0.01, etc.
- Hypothesized Population Parameter Values: Under H₀ (e.g., a hypothesized mean or proportion).
- Sample Size (n): Critical for test sensitivity (power).
- Effect Size: The minimum meaningful difference or association.
- Power Analysis: Often conducted before data collection to ensure the chosen sample size n is sufficient to detect an effect size δ with high probability (commonly 80% power) at the given α.
- Outputs and Decision Criteria:
- Test Statistic: A numerical summary (e.g., t-value, Z-score, F-statistic, chi-square) that measures the divergence of the data from H₀ in a standardized way.
- P-Value: The probability, under the assumption that H₀ is true, of observing a test statistic as extreme as (or more extreme than) the one obtained.
- Critical Value/Region: Involves determining a threshold (or region) for the test statistic based on α and the known sampling distribution under H₀.
- Rejection Region: If the test statistic falls beyond the critical value, H₀ is rejected.
- Acceptance Region: If it falls within this region, H₀ is not rejected.
- Binary Decision: Either reject H₀ (concluding the sample provides statistically significant evidence for H₁) or fail to reject H₀ (concluding the evidence is insufficient).
- Best Practices:
- Report a confidence interval for the parameter of interest.
- Report an effect size measure to convey the estimate and practical significance of any effect.
- Assumptions and Requirements:
- Well-Defined Hypotheses: The null and alternative hypothesis must be mutually exclusive and collectively exhaustive.
- One-Tailed Tests: H₁ posits a direction of effect (e.g., μ > 0).
- Two-Tailed Tests: H₁ only posits a difference without direction (e.g., μ ≠ 0).
- Test Statistic and Distribution: One must choose an appropriate test statistic whose sampling distribution under H₀ is known (at least approximately).
- Significance Level (Type I Error Control): The test procedure is designed such that the probability of a Type I error (incorrectly rejecting a true H₀) is equal to the chosen α.
- Assumptions of Data Generating Process:
- Independence: No unmodeled dependencies between samples.
- Normality: Of the distribution (for parametric tests like t-tests or ANOVA, especially in small samples).
- Homoscedasticity: Equal variances across groups for tests comparing means.
- Decision Rule: A clear decision rule must be defined, based on the test statistic and significance level, to determine when to reject H₀.
- Well-Defined Hypotheses: The null and alternative hypothesis must be mutually exclusive and collectively exhaustive.
- Procedure:
- Formulate Hypotheses: Clearly define the null hypothesis H₀ and alternative hypothesis H₁ for the question at hand.
- Choose Significance Level α: Decide on the significance level (Type I error rate) for the test (e.g., 0.05).
- Select Test and Verify Assumptions: Based on the data type, sample design, and hypotheses, select a suitable statistical test.
- Compute Test Statistic: Using the sample data, calculate the test statistic according to the test's formula.
- Determine P-value or Critical Value: Based on the test statistic and the null distribution, find the p-value.
- Make Decision: Compare the p-value to α (or the test statistic to the critical value) and apply the decision rule.
- If p-value ≤ α: Reject H₀. The result is statistically significant.
- If p-value > α: Fail to reject H₀. The result is not statistically significant.
- Draw Conclusion in Context: Interpret the statistical decision in the context of the original research question.
- Error Types:
- Type I Error: Occurs if we wrongly reject a true H₀ (false positive), which happens with probability α by design.
- Type II Error: Occurs if we fail to reject H₀ when H₀ is false (false negative), with probability denoted β.
- Power: The power of the test is 1-β, the probability of correctly rejecting H₀ when a specific alternative is true.
- Classification of Hypothesis Tests:
- Parametric vs Non-Parametric Tests:
- Parametric Tests: Assume the data follow a certain distribution (often normal distribution) and typically involve parameters like means and variances.
- Non-Parametric Tests: Make fewer assumptions about the distribution; instead of using means and variances, often use ranks or other functions of the data.
- One-Sample, Two-Sample, or Multiple-Sample Tests:
- One-Sample Test: Compares sample to population benchmark.
- Two-Sample Test: Compares two independent samples.
- Paired Test: Compares two dependent observations per subject.
- k-Sample Test: Compares k≥3 groups.
- Directional vs Non-Directional Tests:
- Two-Tailed Test: Used when interested in any difference from H₀, in either direction.
- One-Tailed Test: Used when H₁ specifies a direction of the effect.
- Univariate vs Multivariate Tests:
- Univariate Tests: Examine hypotheses about a single response variable at a time.
- Multivariate Tests: Involve multiple dependent variables being tested simultaneously.
- Fixed-Sample vs Sequential Tests:
- Fixed-Sample Tests: The sample size is decided in advance and the hypothesis is tested only once after all data are collected.
- Sequential Tests: Allow data to be evaluated as they are collected, with the possibility of stopping the experiment early.
- Exact vs Asymptotic Tests:
- Exact Tests: The test statistic's distribution under H₀ is evaluated exactly without relying on large-sample approximations.
- Asymptotic Tests: Use formulas that are derived under the limit of large n.
- Parametric vs Non-Parametric Tests:
- Common Examples of Hypothesis Tests:
- Tests for Differences in Location (Mean or Median):
- One-Sample t-Test: Tests if a sample mean equals a given value.
- Two-Sample t-Test: Tests if two independent samples have the same mean.
- Paired t-Test: Tests if the mean of paired differences is zero.
- Mann-Whitney U Test: Compares two independent samples in terms of distribution/median.
- Wilcoxon Signed-Rank Test: Compares paired observations.
- Kruskal-Wallis Test: Generalization of Mann-Whitney to k independent groups.
- Tests for Distributional Fit or Association:
- Chi-Square Goodness-of-Fit Test: Checks if categorical data match an expected distribution.
- Kolmogorov-Smirnov Test: Checks if a continuous sample comes from a specific distribution.
- Chi-Square Test of Independence: Assesses whether two categorical variables are independent.
- Fisher's Exact Test: Serves the same purpose for small sample contingency tables.
- Variance and Dispersion Tests:
- F-Test: For comparing variance of two samples.
- Levene's Test: For comparing variances across multiple groups.
- One-Way ANOVA: Tests if any group mean differs in a single-factor experiment.
- Two-Way ANOVA: Tests effects of two factors on a continuous outcome.
- Correlation and Regression Significance Tests:
- Pearson Correlation Test: Examines if there is a non-zero linear correlation between two continuous variables.
- Spearman Rank Correlation Test: Does similarly for rank-order correlation.
- Regression Coefficient Tests: In regression analysis, hypothesis tests are used for model parameters.
- Tests for Differences in Location (Mean or Median):
- Multiple Comparisons and Error Control:
- Multiple Comparisons Problem: Performing multiple hypothesis tests in the same study can greatly inflate the chance of false positives (Type I errors) if not addressed.
- Family-Wise Error Rate (FWER): The probability that at least one null hypothesis is wrongly rejected.
- False Discovery Rate (FDR): The expected proportion of false discoveries among the rejected hypotheses.
- Multiple Testing Correction Procedures:
- Bonferroni Correction: Adjusts the significance threshold to α/m when m tests are performed.
- Holm's Procedure: A less conservative alternative to Bonferroni.
- Benjamini-Hochberg Procedure: Controls the false discovery rate.
- Practical Significance vs Statistical Significance:
- Statistical Significance: A result where p < α, indicating the effect is unlikely due to chance.
- Practical Significance: Whether the magnitude of the effect is big enough to matter in practice.
- Effect Size Reporting: Important for distinguishing a result that is statistically significant from one that is also practically significant.
- Confidence Interval Reporting: Provides a range of plausible values for the population parameter consistent with the data.
- Near-Related Concepts (Counter-Examples):
- Exploratory Data Analysis (EDA): Unlike confirmatory hypothesis testing, EDA involves looking at data without a pre-specified hypothesis.
- Statistical Parameter Estimation: Estimation (finding point estimates and confidence intervals for population parameters) is a distinct task from hypothesis testing.
- Order Statistics or Descriptive Statistics: Simply computing order statistics or other descriptive measures from a sample is not a hypothesis test.
- Predictive Modeling and Machine Learning Evaluation: Tasks like building a predictive model and evaluating its performance are not hypothesis tests in themselves.
- Bayesian Analysis (Bayes Factors): Bayesian hypothesis testing replaces p-values with Bayes factors or posterior probabilities of hypotheses.
- Core Components:
- Citations:
[1] http://www.gabormelli.com/RKB/Statistical_Hypothesis_Testing_Task [2] https://www.ebsco.com/research-starters/science/statistical-hypothesis-testing [3] https://www.itl.nist.gov/div898/handbook/prc/section1/prc13.htm [4] https://blog.minitab.com/en/quality-business/common-assumptions-about-data-part-2-normality-and-equal-variance [5] https://www.scribbr.com/statistics/statistical-power/ [6] https://www.scribbr.com/statistics/type-i-and-type-ii-errors/ [7] https://online.stat.psu.edu/stat200/lesson/11/11.2/11.2.1 [8] https://statisticsbyjim.com/hypothesis-testing/practical-statistical-significance/ [9] https://www.statisticssolutions.com/should-you-use-a-one-tailed-test-or-a-two-tailed-test-for-your-data-analysis/ [10] https://www.skillsyouneed.com/num/hypotheses-testing.html [11] https://stats.oarc.ucla.edu/other/mult-pkg/faq/general/faq-what-are-the-differences-between-one-tailed-and-two-tailed-tests/ [12] https://stats.stackexchange.com/questions/297084/what-is-the-definition-of-multivariate-testing [13] https://statisticsbyjim.com/anova/multivariate-anova-manova-benefits-use/ [14] https://amplitude.com/blog/sequential-test-vs-t-test [15] https://pmc.ncbi.nlm.nih.gov/articles/PMC5426219/ [16] https://stats.stackexchange.com/questions/483472/why-are-exact-tests-preferred-over-chi-squared-for-small-sample-sizes [17] https://en.wikipedia.org/wiki/Multiple_comparisons_problem
2017a
- (Changing Works, 2017) ⇒ Retrieved on 2017-05-07 from http://changingminds.org/explanations/research/analysis/parametric_non-parametric.htm Copyright: Changing Works 2002-2016
- There are two types of test data and consequently different types of analysis. As the table below shows, parametric data has an underlying normal distribution which allows for more conclusions to be drawn as the shape can be mathematically described. Anything else is non-parametric.
Parametric Statistical Tests Non-Parametric Statistical Tests Assumed distribution Normally Distributed Any Assumed variance Homogeneous Any Typical data Ratio or Interval Ordinal or Nominal Data set relationships Independent Any Usual central measure Mean Median Benefits Can draw more conclusions Simplicity; Less affected by outliers
2017b
- (Jim Frost, 2015) ⇒ Retrieved on 2017-05-07 from http://blog.minitab.com/blog/adventures-in-statistics-2/choosing-between-a-nonparametric-test-and-a-parametric-test Copyright ©2017 Minitab Inc. All rights Reserved.
- Nonparametric tests are like a parallel universe to parametric tests. The table shows related pairs of hypothesis tests that Minitab statistical software offers.
Parametric tests (means) Nonparametric tests (medians) 1-sample t test 1-sample Sign, 1-sample Wilcoxon 2-sample t test Mann-Whitney test One-Way ANOVA Kruskal-Wallis, Mood’s median test Factorial DOE with one factor and one blocking variable Friedman test
2017c
- (Surbhi, 2016) ⇒ Retrived on 2017-05-07 from http://keydifferences.com/difference-between-parametric-and-nonparametric-test.html Copyright © 2017 KeyDifferences
PARAMETRIC TEST NON-PARAMETRIC TEST Independent Sample t Test Mann-Whitney test Paired samples t test Wilcoxon signed Rank test One way Analysis of Variance (ANOVA) Kruskal Wallis Test One way repeated measures Analysis of Variance Friedman's ANOVA
2016A
- (Wikipedia, 2016) ⇒ https://en.wikipedia.org/wiki/Statistical_hypothesis_testing Retrieved:2016-5-24.
- A statistical hypothesis is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables. A statistical hypothesis test is a method of statistical inference. Commonly, two statistical data sets are compared, or a data set obtained by sampling is compared against a synthetic data set from an idealized model. A hypothesis is proposed for the statistical relationship between the two data sets, and this is compared as an alternative to an idealized null hypothesis that proposes no relationship between two data sets. The comparison is deemed statistically significant if the relationship between the data sets would be an unlikely realization of the null hypothesis according to a threshold probability—the significance level. Hypothesis tests are used in determining what outcomes of a study would lead to a rejection of the null hypothesis for a pre-specified level of significance. The process of distinguishing between the null hypothesis and the alternative hypothesis is aided by identifying two conceptual types of errors (type 1 & type 2), and by specifying parametric limits on e.g. how much type 1 error will be permitted. An alternative framework for statistical hypothesis testing is to specify a set of statistical models, one for each candidate hypothesis, and then use model selection techniques to choose the most appropriate model. The most common selection techniques are based on either Akaike information criterion or Bayes factor.
Statistical hypothesis testing is sometimes called confirmatory data analysis. It can be contrasted with exploratory data analysis, which may not have pre-specified hypotheses.
- A statistical hypothesis is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables. A statistical hypothesis test is a method of statistical inference. Commonly, two statistical data sets are compared, or a data set obtained by sampling is compared against a synthetic data set from an idealized model. A hypothesis is proposed for the statistical relationship between the two data sets, and this is compared as an alternative to an idealized null hypothesis that proposes no relationship between two data sets. The comparison is deemed statistically significant if the relationship between the data sets would be an unlikely realization of the null hypothesis according to a threshold probability—the significance level. Hypothesis tests are used in determining what outcomes of a study would lead to a rejection of the null hypothesis for a pre-specified level of significance. The process of distinguishing between the null hypothesis and the alternative hypothesis is aided by identifying two conceptual types of errors (type 1 & type 2), and by specifying parametric limits on e.g. how much type 1 error will be permitted. An alternative framework for statistical hypothesis testing is to specify a set of statistical models, one for each candidate hypothesis, and then use model selection techniques to choose the most appropriate model. The most common selection techniques are based on either Akaike information criterion or Bayes factor.
2016B
- (Minitab, 2016) ⇒ http://support.minitab.com/en-us/minitab/17/topic-library/basic-statistics-and-graphs/hypothesis-tests/basics/what-is-a-hypothesis-test/
- A hypothesis test is a statistical test that is used to determine whether there is enough evidence in a sample of data to infer that a certain condition is true for the entire population.
- A hypothesis test examines two opposing hypotheses about a population: the null hypothesis and the alternative hypothesis. The null hypothesis is the statement being tested. Usually the null hypothesis is a statement of "no effect" or "no difference". The alternative hypothesis is the statement you want to be able to conclude is true.
- Based on the sample data, the test determines whether to reject the null hypothesis. You use a p-value, to make the determination. If the p-value is less than or equal to the level of significance, which is a cut-off point that you define, then you can reject the null hypothesis.
- A common misconception is that statistical hypothesis tests are designed to select the more likely of two hypotheses. Instead, a test will remain with the null hypothesis until there is enough evidence (data) to support the alternative hypothesis.
- Examples of questions you can answer with a hypothesis test include:
- Does the mean height of undergraduate women differ from 66 inches?
- Is the standard deviation of their height equal less than 5 inches?
- Do male and female undergraduates differ in height?
2016C
- (Wikipedia, 2016) ⇒ https://en.wikipedia.org/wiki/Location_test#Parametric_and_nonparametric_location_tests
- The following table summarizes some common parametric and nonparametric tests for the means of one or more samples.
Ordinal and numerical measures 1 group N ≥ 30 One-sample t-test N < 30 Normally distributed One-sample t-test Not normal Sign test 2 groups Independent N ≥ 30 t-test N < 30 Normally distributed t-test Not normal Mann–Whitney U or Wilcoxon rank-sum test Paired N ≥ 30 paired t-test N < 30 Normally distributed paired t-test Not normal Wilcoxon signed-rank test 3 or more groups Independent Normally distributed 1 factor One way anova ≥ 2 factors two or other anova Not normal Kruskal–Wallis one-way analysis of variance by ranks Dependent Normally distributed Repeated measures anova Not normal Friedman two-way analysis of variance by ranks
Nominal measures 1 group np and n(1-p) ≥ 5 Z-approximation np or n(1-p) < 5 binomial 2 groups Independent np < 5 fisher exact test np ≥ 5 chi-squared test Paired McNemar or Kappa 3 or more groups Independent np < 5 collapse categories for chi-squared test np ≥ 5 chi-squared test Dependent Cochran´s Q
2012
- Eric W. Weisstein. “Hypothesis Testing." From MathWorld -- A Wolfram Web Resource. http://mathworld.wolfram.com/HypothesisTesting.html
- Hypothesis testing is the use of statistics to determine the probability that a given hypothesis is true. The usual process of hypothesis testing consists of four steps.
- Formulate the null hypothesis [math]\displaystyle{ H_0 }[/math] (commonly, that the observations are the result of pure chance) and the alternative hypothesis [math]\displaystyle{ H_a }[/math] (commonly, that the observations show a real effect combined with a component of chance variation).
- Identify a test statistic that can be used to assess the truth of the null hypothesis.
- Compute the P-value, which is the probability that a test statistic at least as significant as the one observed would be obtained assuming that the null hypothesis were true. The smaller the P-value, the stronger the evidence against the null hypothesis.
- Compare the p-value to an acceptable significance value alpha (sometimes called an alpha value). If p<=alpha, that the observed effect is statistically significant, the null hypothesis is ruled out, and the alternative hypothesis is valid.
- Hypothesis testing is the use of statistics to determine the probability that a given hypothesis is true. The usual process of hypothesis testing consists of four steps.
2010
- (Siegfried, 2010) ⇒ Tom Siegfried. (2010). “Are, Its Wrong: Science fails to face the shortcomings of statistics.” In: Science News, 177(7).
- http://www.psychology.emory.edu/clinical/bliwise/Tutorials/CHTESTS/choose/nom.htm
- QUOTE: The following tests can be used with nominal data. Which test you select is determined by the number of samples and whether you are testing an hypothesis about group differences or the association between independent and dependent variables. If you are testing an hypothesis about group differences, you also must consider whether the groups/samples are independent or dependent
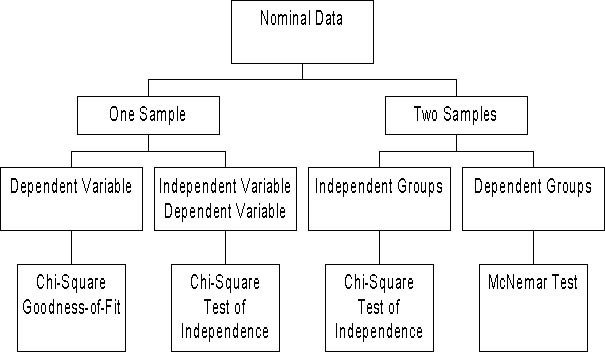
- QUOTE: The following tests can be used with nominal data. Which test you select is determined by the number of samples and whether you are testing an hypothesis about group differences or the association between independent and dependent variables. If you are testing an hypothesis about group differences, you also must consider whether the groups/samples are independent or dependent
2006
- (Dubnicka, 2006k) ⇒ Suzanne R. Dubnicka. (2006). “Introduction to Statistics - Handout 11." Kansas State University, Introduction to Probability and Statistics I, STAT 510 - Fall 2006.
- QUOTE: ... Estimation and hypothesis testing are the two common forms of statistical inference. ... In hypothesis testing, we are trying to answer a yes/no question regarding the parameter of interest. For example, we might want ask, “Is the parameter larger than a specified value?” Hypothesis testing often uses the point estimate and its standard error to answer the question of interest?
2003
- http://www.nature.com/nrg/journal/v4/n9/glossary/nrg1155_glossary.html
- QUOTE: ... A test statistic is a statistic that is used in a statistical test to discriminate between two competing hypotheses, the so-called null and alternative hypotheses.
1991
- (Efron & Tibshirani, 1991) ⇒ Bradley Efron, and Robert Tibshirani. (1991). “Statistical Data Analysis in the Computer Age.” In: Science, 253(5018). 10.1126/science.253.5018.390
- QUOTE: Most of our familiar statistical methods, such as hypothesis testing, linear regression, analysis of variance, and maximum likelihood estimation, were designed to be implemented on mechanical calculators. ...
1960
- (Wason, 1960) ⇒ Peter C. Wason. (1960). “On the Failure to Eliminate Hypotheses in a Conceptual Task." Quarterly journal of experimental psychology 12, no. 3 doi:10.1080/17470216008416717
- QUOTE: This investigation examines the extent to which intelligent young adults seek (i) confirming evidence alone (enumerative induction) or (ii) confirming and discontinuing evidence (eliminative induction), in order to draw conclusions in a simple conceptual task. The experiment is designed so that use of confirming evidence alone will almost certainly lead to erroneous conclusions because (i) the correct concept is entailed by many more obvious ones, and (ii) the universe of possible instances (numbers) is infinite.
Six out of 29 subjects reached the correct conclusion without previous incorrect ones, 13 reached one incorrect conclusion, nine reached two or more incorrect conclusions, and one reached no conclusion. The results showed that those subjects, who reached two or more incorrect conclusions, were unable, or unwilling to test their hypotheses. The implications are discussed in relation to scientific thinking.
- QUOTE: This investigation examines the extent to which intelligent young adults seek (i) confirming evidence alone (enumerative induction) or (ii) confirming and discontinuing evidence (eliminative induction), in order to draw conclusions in a simple conceptual task. The experiment is designed so that use of confirming evidence alone will almost certainly lead to erroneous conclusions because (i) the correct concept is entailed by many more obvious ones, and (ii) the universe of possible instances (numbers) is infinite.