Directed Graph

A directed graph is a graph whose graph edges are all directed graph edges.

• AKA: Digraph.
• Context:
  • It can range from being a Directed Acyclic Graph(DAG) to being a Directed Cyclic Graph.
  • It can range from being an Unlabeled Directed Graph to being a Labeled Directed Graph.
  • It can be represented by a Directed Graph Dataset.
  • It can (typically) have Children Nodes
  • It can have:
    • zero or more Root Nodes (such as parent nodes)
    • zero or more Children Nodes, ranging from Intermediate Nodes to being Leaf Nodes
• Example(s):
  • a Hasse Diagram.
  • a Bayesian Network.
  • a Hidden Markov Model.
  • a Citation Network.
  • a Hierarchical Directed Acyclic Graph.
  • special cases: a Directed Sequence, a Directed Tree, a Directed Lattice.
  • …
• Counter-Example(s):
  • a Undirected Graph.
  • A Digram
• See: Partial Order Relation, Directed Network, Graph Theory, Ordered Pair, Multigraph, Multiset.

---

---

References

2013

• (Wikipedia, 2013) ⇒ http://en.wikipedia.org/wiki/directed_graph Retrieved:2013-12-8.
  • In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph, or set of nodes connected by edges, where the edges have a direction associated with them. In formal terms, a digraph is a pair [math]G=(V,A)[/math] (sometimes [math]G=(V,E)[/math]) of:
    • a set V, whose elements are called vertices or nodes,
    • a set A of ordered pairs of vertices, called arcs, directed edges, or arrows (and sometimes simply edges with the corresponding set named E instead of A).

      It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called edges.

      Sometimes a digraph is called a simple digraph to distinguish it from a directed multigraph, in which the arcs constitute a multiset, rather than a set, of ordered pairs of vertices. Also, in a simple digraph loops are disallowed. (A loop is an arc that pairs a vertex to itself.) On the other hand, some texts allow loops, multiple arcs, or both in a digraph.

2011

• (Sammut & Webb, 2011) ⇒ Claude Sammut (editor), and Geoffrey I. Webb (editor). (2011). “Digraphs.” In: (Sammut & Webb, 2011)
  • Synonyms: Directed graphs

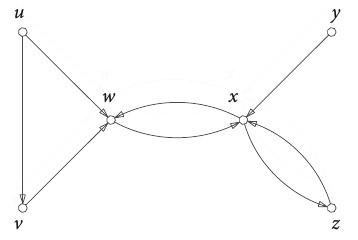
    Definition: A digraph [math]D[/math] consists of a (finite) set of vertices [math]V(D)[/math] and a set [math]A(D)[/math] of ordered pairs, called arcs, of distinct vertices. An arc [math](u,\; v)[/math] has tail [math]u[/math] and head [math]v[/math], and it is said to leave [math]u[/math] and enter [math]v[/math].

    Figure 1 shows a digraph [math]D[/math] with vertex set [math]V(D)=\{ u,\; v,\; w,\; x,\; y,\;z\}[/math] and arc set [math]A(D)=\{ (u, v), (u, w), (v, w), (w, x), (x, w), (x,z), (y, x) (z,x)\}[/math]. Digraphs can be viewed as generalizations of graphs.

    

    Digraphs, Fig. 1: A digraph.

---