Directed Graph
A directed graph is a graph whose graph edges are all directed graph edges.
- AKA: Digraph.
- Context:
- It can range from being a Directed Acyclic Graph(DAG) to being a Directed Cyclic Graph.
- It can range from being an Unlabeled Directed Graph to being a Labeled Directed Graph.
- It can be represented by a Directed Graph Dataset.
- It can (typically) have Children Nodes.
- It can have:
- zero or more Root Nodes (such as parent nodes)
- zero or more Children Nodes, ranging from Intermediate Nodes to being Leaf Nodes
- Example(s):
- a Hasse Diagram.
- a Bayesian Network.
- a Hidden Markov Model.
- a Citation Network.
- a Hierarchical Directed Acyclic Graph.
- special cases: a Directed Sequence, a Directed Tree, a Directed Lattice.
- …
- Counter-Example(s):
- a Undirected Graph.
- A Digram.
- See: Partial Order Relation, Directed Network, Graph Theory, Ordered Pair, Multigraph, Multiset.
References
2013
- (Wikipedia, 2013) ⇒ http://en.wikipedia.org/wiki/directed_graph Retrieved:2013-12-8.
- In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph, or set of nodes connected by edges, where the edges have a direction associated with them. In formal terms, a digraph is a pair [math]\displaystyle{ G=(V,A) }[/math] (sometimes [math]\displaystyle{ G=(V,E) }[/math]) of: [1]
- a set V, whose elements are called vertices or nodes,
- a set A of ordered pairs of vertices, called arcs, directed edges, or arrows (and sometimes simply edges with the corresponding set named E instead of A).
It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called edges.
Sometimes a digraph is called a simple digraph to distinguish it from a directed multigraph, in which the arcs constitute a multiset, rather than a set, of ordered pairs of vertices. Also, in a simple digraph loops are disallowed. (A loop is an arc that pairs a vertex to itself.) On the other hand, some texts allow loops, multiple arcs, or both in a digraph.
- In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph, or set of nodes connected by edges, where the edges have a direction associated with them. In formal terms, a digraph is a pair [math]\displaystyle{ G=(V,A) }[/math] (sometimes [math]\displaystyle{ G=(V,E) }[/math]) of: [1]
- ↑ . , Section 1.10. , Section 10.
2011
- (Sammut & Webb, 2011) ⇒ Claude Sammut (editor), and Geoffrey I. Webb (editor). (2011). “Digraphs.” In: (Sammut & Webb, 2011)
- Synonyms: Directed graphs
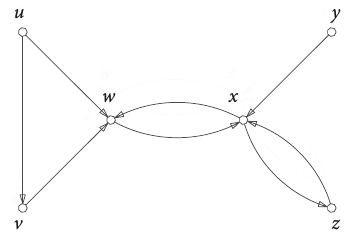
Definition: A digraph [math]\displaystyle{ D }[/math] consists of a (finite) set of vertices [math]\displaystyle{ V(D) }[/math] and a set [math]\displaystyle{ A(D) }[/math] of ordered pairs, called arcs, of distinct vertices. An arc [math]\displaystyle{ (u,\; v) }[/math] has tail [math]\displaystyle{ u }[/math] and head [math]\displaystyle{ v }[/math], and it is said to leave [math]\displaystyle{ u }[/math] and enter [math]\displaystyle{ v }[/math].
Figure 1 shows a digraph [math]\displaystyle{ D }[/math] with vertex set [math]\displaystyle{ V(D)=\{ u,\; v,\; w,\; x,\; y,\;z\} }[/math] and arc set [math]\displaystyle{ A(D)=\{ (u, v), (u, w), (v, w), (w, x), (x, w), (x,z), (y, x) (z,x)\} }[/math]. Digraphs can be viewed as generalizations of graphs.
Digraphs, Fig. 1: A digraph.
- Synonyms: Directed graphs