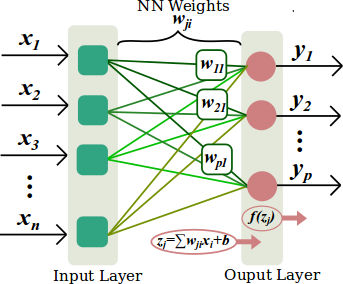
Single Layer Neural Network
An Single Layer Neural Network is an Artificial Neural Network with no Hidden Neural Network Layers.
- AKA: 1-Layer Neural Network.
- Context:
- It is only composed of a Neural Network Input Layer and a Neural Network Output Layer.
- It can be trained using a Single Layer ANN Training System (that solves by a Single Layer ANN Training Task by implementing a Single Layer ANN Training Algorithm).
- It can be graphically represented as:
- It can mathematically described by a Single Layer Artificial Neural Network Model where the j-th element of the Neural Network Output Vector is given by:
[math]\displaystyle{ y_j= f(\displaystyle\sum_{i=0}^nw_{ji}x_i+b) }[/math],
[math]\displaystyle{ x_i }[/math] is the i-th element of the Neural Network Input Vector, [math]\displaystyle{ w_{ji} }[/math] is the Neural Network Weight Matrix, [math]\displaystyle{ b }[/math] is the Bias Neuron, and [math]\displaystyle{ f }[/math] is a Neural Activation Function.
- …
- Example(s):
- a Single Layer Perceptron,
- Linear Classifiers such as: a binary softmax classifier, or a binary SVM classifier.
- …
- Counter-Example(s):
- See: Artificial Neural Network, Neural Network Layer, Artificial Neuron, Neuron Activation Function, Neural Network Topology.
References
2018
- (CS231n, 2018) ⇒ Single neuron as a linear classifier. In: CS231n Convolutional Neural Networks for Visual Recognition Retrieved: 2018-01-14.
- QUOTE: The mathematical form of the model Neuron’s forward computation might look familiar to you. As we saw with linear classifiers, a neuron has the capacity to “like” (activation near one) or “dislike” (activation near zero) certain linear regions of its input space. Hence, with an appropriate loss function on the neuron’s output, we can turn a single neuron into a linear classifier:
- Binary Softmax classifier. For example, we can interpret [math]\displaystyle{ \sigma(\sum_{i=0}^nw_ix_i+b) }[/math] to be the probability of one of the classes [math]\displaystyle{ P(yi=1∣xi;w) }[/math]. The probability of the other class would be [math]\displaystyle{ P(yi=0∣xi;w)=1−P(yi=1∣xi;w) }[/math], since they must sum to one. With this interpretation, we can formulate the cross-entropy loss as we have seen in the Linear Classification section, and optimizing it would lead to a binary Softmax classifier (also known as logistic regression). Since the sigmoid function is restricted to be between 0-1, the predictions of this classifier are based on whether the output of the neuron is greater than 0.5.
- Binary SVM classifier. Alternatively, we could attach a max-margin hinge loss to the output of the neuron and train it to become a binary Support Vector Machine.
- Regularization interpretation. The regularization loss in both SVM/Softmax cases could in this biological view be interpreted as gradual forgetting, since it would have the effect of driving all synaptic weights ww towards zero after every parameter update.
- QUOTE: The mathematical form of the model Neuron’s forward computation might look familiar to you. As we saw with linear classifiers, a neuron has the capacity to “like” (activation near one) or “dislike” (activation near zero) certain linear regions of its input space. Hence, with an appropriate loss function on the neuron’s output, we can turn a single neuron into a linear classifier:
2005
- (Golda, 2005) ⇒ Adam Gołda (2005). Introduction to neural networks. AGH-UST.
- QUOTE: There are different types of neural networks, which can be distinguished on the basis of their structure and directions of signal flow. Each kind of neural network has its own method of training. Generally, neural networks may be differentiated as follows:
- feedforward networks
- one-layer networks
- multi-layer networks
- recurrent networks
- cellular networks.
Feedforward neural networks, which typical example is one-layer perceptron (see figure of Single-layer perceptron), consist of neurons set in layers. The information flow has one direction. Neurons from a layer are connected only with the neurons from the preceding layer. The multi-layer networks usually consist of input, hidden (one or more), and output layers. Such system may be treated as non-linear function approximation block: y = f(u).
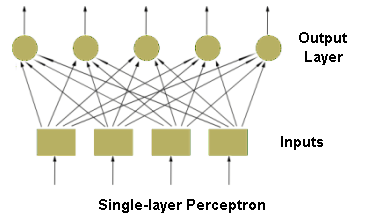
- QUOTE: There are different types of neural networks, which can be distinguished on the basis of their structure and directions of signal flow. Each kind of neural network has its own method of training. Generally, neural networks may be differentiated as follows:
1943
- (McCulloch & Pitts, 1943) ⇒ McCulloch, W. S., & Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. The bulletin of mathematical biophysics, 5(4), 115-133.
- ABSTRACT: Because of the “all-or-none” character of nervous activity, neural events and the relations among them can be treated by means of propositional logic. It is found that the behavior of every net can be described in these terms, with the addition of more complicated logical means for nets containing circles; and that for any logical expression satisfying certain conditions, one can find a net behaving in the fashion it describes. It is shown that many particular choices among possible neurophysiological assumptions are equivalent, in the sense that for every net behaving under one assumption, there exists another net which behaves under the other and gives the same results, although perhaps not in the same time. Various applications of the calculus are discussed.