Neural Network Memory Cell
A Neural Network Memory Cell is a Neural Network Cell that can be activated by an Attention Mechanism.
- AKA: Neural Network Memory Block.
- Context:
- It can range from being a Neural Network Internal Memory Cell to being a Neural Network External Memory Cell.
- Example(s):
- Counter-Example(s):
- See: Artificial Neural Network, Artificial Neuron, Neural Network Activation Function, Neural Network Hidden Layer.
References =
2018a
- (Wikipedia, 2018) ⇒ https://en.wikipedia.org/wiki/long_short-term_memory Retrieved:2018-3-27.
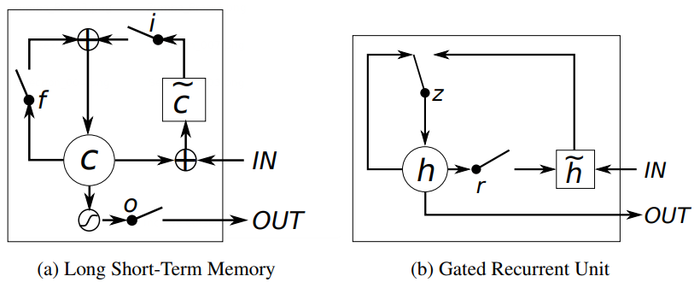
- Long short-term memory (LSTM) units (or blocks) are a building unit for layers of a recurrent neural network (RNN). A RNN composed of LSTM units is often called an LSTM network. A common LSTM unit is composed of a cell, an input gate, an output gate and a forget gate. The cell is responsible for "remembering" values over arbitrary time intervals; hence the word "memory" in LSTM. Each of the three gates can be thought of as a "conventional" artificial neuron, as in a multi-layer (or feedforward) neural network: that is, they compute an activation (using an activation function) of a weighted sum. Intuitively, they can be thought as regulators of the flow of values that goes through the connections of the LSTM; hence the denotation "gate". There are connections between these gates and the cell.
The expression long short-term refers to the fact that LSTM is a model for the short-term memory which can last for a long period of time. An LSTM is well-suited to classify, process and predict time series given time lags of unknown size and duration between important events. LSTMs were developed to deal with the exploding and vanishing gradient problem when training traditional RNNs. Relative insensitivity to gap length gives an advantage to LSTM over alternative RNNs, hidden Markov models and other sequence learning methods in numerous applications.
- Long short-term memory (LSTM) units (or blocks) are a building unit for layers of a recurrent neural network (RNN). A RNN composed of LSTM units is often called an LSTM network. A common LSTM unit is composed of a cell, an input gate, an output gate and a forget gate. The cell is responsible for "remembering" values over arbitrary time intervals; hence the word "memory" in LSTM. Each of the three gates can be thought of as a "conventional" artificial neuron, as in a multi-layer (or feedforward) neural network: that is, they compute an activation (using an activation function) of a weighted sum. Intuitively, they can be thought as regulators of the flow of values that goes through the connections of the LSTM; hence the denotation "gate". There are connections between these gates and the cell.
2018b
- (CS231n, 2018) ⇒ Biological motivation and connections. In: CS231n Convolutional Neural Networks for Visual Recognition Retrieved: 2018-01-14.
- QUOTE: The basic computational unit of the brain is a neuron. Approximately 86 billion neurons can be found in the human nervous system and they are connected with approximately [math]\displaystyle{ 10^{14} - 10^{15} }[/math] synapses. The diagram below shows a cartoon drawing of a biological neuron (left) and a common mathematical model (right). Each neuron receives input signals from its dendrites and produces output signals along its (single) axon. The axon eventually branches out and connects via synapses to dendrites of other neurons. In the computational model of a neuron, the signals that travel along the axons (e.g. [math]\displaystyle{ x_0 }[/math]) interact multiplicatively (e.g. [math]\displaystyle{ w_0x_0 }[/math]) with the dendrites of the other neuron based on the synaptic strength at that synapse (e.g. [math]\displaystyle{ w_0 }[/math]). The idea is that the synaptic strengths (the weights [math]\displaystyle{ w }[/math]) are learnable and control the strength of influence (and its direction: excitory (positive weight) or NN Inhibitoryinhibitory (negative weight) of one neuron on another. In the basic model, the dendrites carry the signal to the cell body where they all get summed. If the final sum is above a certain threshold, the neuron can fire, sending a spike along its axon. In the computational model, we assume that the precise timings of the spikes do not matter, and that only the frequency of the firing communicates information. Based on this rate code interpretation, we model the firing rate of the neuron with an activation function [math]\displaystyle{ f }[/math], which represents the frequency of the spikes along the axon. Historically, a common choice of activation function is the sigmoid function [math]\displaystyle{ \sigma }[/math], since it takes a real-valued input (the signal strength after the sum) and squashes it to range between 0 and 1. We will see details of these activation functions later in this section.
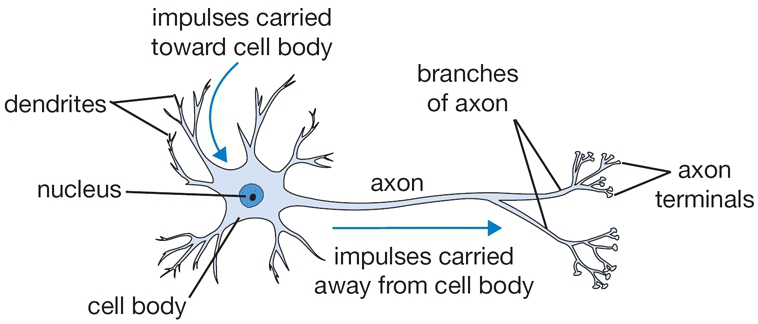
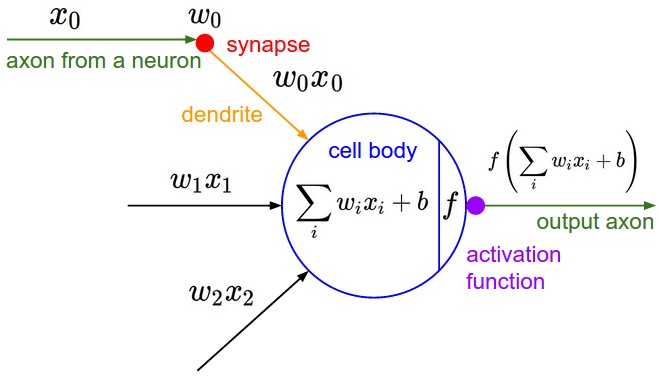
A cartoon drawing of a biological neuron (left) and its mathematical model (right).
- QUOTE: The basic computational unit of the brain is a neuron. Approximately 86 billion neurons can be found in the human nervous system and they are connected with approximately [math]\displaystyle{ 10^{14} - 10^{15} }[/math] synapses. The diagram below shows a cartoon drawing of a biological neuron (left) and a common mathematical model (right). Each neuron receives input signals from its dendrites and produces output signals along its (single) axon. The axon eventually branches out and connects via synapses to dendrites of other neurons. In the computational model of a neuron, the signals that travel along the axons (e.g. [math]\displaystyle{ x_0 }[/math]) interact multiplicatively (e.g. [math]\displaystyle{ w_0x_0 }[/math]) with the dendrites of the other neuron based on the synaptic strength at that synapse (e.g. [math]\displaystyle{ w_0 }[/math]). The idea is that the synaptic strengths (the weights [math]\displaystyle{ w }[/math]) are learnable and control the strength of influence (and its direction: excitory (positive weight) or NN Inhibitoryinhibitory (negative weight) of one neuron on another. In the basic model, the dendrites carry the signal to the cell body where they all get summed. If the final sum is above a certain threshold, the neuron can fire, sending a spike along its axon. In the computational model, we assume that the precise timings of the spikes do not matter, and that only the frequency of the firing communicates information. Based on this rate code interpretation, we model the firing rate of the neuron with an activation function [math]\displaystyle{ f }[/math], which represents the frequency of the spikes along the axon. Historically, a common choice of activation function is the sigmoid function [math]\displaystyle{ \sigma }[/math], since it takes a real-valued input (the signal strength after the sum) and squashes it to range between 0 and 1. We will see details of these activation functions later in this section.
2014
- (Chung et al., 2014) ⇒ Junyoung Chung, Caglar Gulcehre, KyungHyun Cho, and Yoshua Bengio (2014). "Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling". arXiv:1412.3555.
- QUOTE: It is easy to notice similarities between the LSTM unit and the GRU from Fig. 1.
The most prominent feature shared between these units is the additive component of their update from t to t + 1, which is lacking in the traditional recurrent unit. The traditional recurrent unit always replaces the activation, or the content of a unit with a new value computed from the current input and the previous hidden state. On the other hand, both LSTM unit and GRU keep the existing content and add the new content on top of it (...)
- QUOTE: It is easy to notice similarities between the LSTM unit and the GRU from Fig. 1.
- Figure 1: Illustration of (a) LSTM and (b) gated recurrent units. (a) [math]\displaystyle{ i }[/math], [math]\displaystyle{ f }[/math] and [math]\displaystyle{ o }[/math] are the input, forget and output gates, respectively. [math]\displaystyle{ c }[/math] and [math]\displaystyle{ \tilde{c} }[/math] denote the memory cell and the new memory cell content. (b) [math]\displaystyle{ r }[/math] and [math]\displaystyle{ z }[/math] are the reset and update gates, and [math]\displaystyle{ h }[/math] and [math]\displaystyle{ \tilde{h} }[/math] are the activation and the candidate activation.