sklearn.linear model.ARDRegression

A sklearn.linear_model.ARDRegression is a ARD Regression System within sklearn.linear_model class.

• AKA: ARDRegression, linear_model.ARDRegression.
• Context
  • Usage:

1) Import ARD Regression model from scikit-learn : from sklearn.linear_model import ARDRegression

2) Create design matrix X and response vector Y

3) Create ARD Regression object: model=ARDRegression([n_iter=n_iter, tol=tol, alpha_1=alpha1, alpha_2=alpha1, lambda_1=lambda1, lambda_2=lambda2,...])

4) Choose method(s):

• Fit the ARDRegression model to the dataset: model.fit(X, Y[, check_input]))
• Predict Y using the linear model with estimated coefficients: Y_pred = model.predict(X)
• Return coefficient of determination (R^2) of the prediction: model.score(X,Y[, sample_weight=w])
• Get estimator parameters: model.get_params([deep])
• Set estimator parameters: model.set_params(**params)

• Example(s):
  • 10-fold sklearn Boston data evaluation [1]

Input:

Output:

#Importing modules from sklearn.linear_model import ARDRegression from sklearn.model_selection import cross_val_predict from sklearn.datasets import load_boston from sklearn.metrics import explained_variance_score, mean_squared_error import numpy as np import pylab as pl boston = load_boston() #Loading boston datasets x = boston.data # Creating Regression Design Matrix y = boston.target # Creating target dataset ARD= ARDRegression(alpha_1=0.01, alpha_2=0.01, lambda_1=1e-06, lambda_2=1e-06) # Create ARD regression object for the hyperparameters alpha1,2=0.01 and lambda1,2=1e-6 ARD.fit(x,y) # predicted values #Calculaton of RMSE and Explained Variances yp_cv = cross_val_predict(ARD, x, y, cv=10) #Calculation 10-Fold CV Evariance=explained_variance_score(y,yp) Evariance_cv=explained_variance_score(y,yp_cv) RMSE =np.sqrt(mean_squared_error(y,yp)) RMSECV =sqrt(mean_squared_error(y,yp_cv) # Printing Results print('Method: ARDRegression Regression') print('RMSE on the dataset: %.4f' %RMSE) print('RMSE on 10-fold CV: %.4f' %RMSECV) print('Explained Variance Regression Score on the dataset: %.4f' %Evariance) print('Explained Variance Regression 10-fold CV: %.4f' %Evariance_cv) #plotting real vs predicted data pl.figure(1) pl.plot(yp, y,'ro') pl.plot(yp_cv, y,'bo', alpha=0.25, label='10-folds CV') pl.xlabel('predicted') pl.title('ARD Regression, alpha1,2=0.01 lambad1,2=1e-6') pl.ylabel('real') pl.grid(True) pl.show()

(blue dots correspond to 10-Fold CV) Method: ARD Regression RMSE on the dataset: 4.7411 RMSE on 10-fold CV: 5.9097 Explained Variance Regression Score on the dataset : 0.7337 Explained Variance Regression 10-fold CV: 0.5863

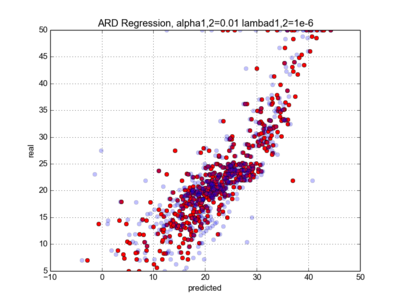
• Counter-Example(s)
  • sklearn.linear_model.LinearRegression.
  • sklearn.linear_model.Lasso
  • sklearn.linear_model.Ridge.
  • sklearn.linear_model.BayesianRidge.
  • sklearn.linear_model.ElasticNet.
  • sklearn.linear_model.HuberRegressor.
  • sklearn.linear_model.Lars.
• See: Explained Variance Regression Score, Regression System, Regularization Task, Bayesian Regression Task, Bayesian Analysis.

---

---

References

2017

• http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.ARDRegression.html
  • QUOTE: class sklearn.linear_model.ARDRegression(n_iter=300, tol=0.001, alpha_1=1e-06, alpha_2=1e-06, lambda_1=1e-06, lambda_2=1e-06, compute_score=False, threshold_lambda=10000.0, fit_intercept=True, normalize=False, copy_X=True, verbose=False)

     :: Bayesian ARD regression.

Fit the weights of a regression model, using an ARD prior. The weights of the regression model are assumed to be in Gaussian distributions. Also estimate the parameters lambda (precisions of the distributions of the weights) and alpha (precision of the distribution of the noise). The estimation is done by an iterative procedures (Evidence Maximization)noise).

---