2008 ExtractingandComposingRobustFea
- (Vincent et al., 2008) ⇒ Pascal Vincent, Hugo Larochelle, Yoshua Bengio, and Pierre-Antoine Manzagol. (2008). “Extracting and Composing Robust Features with Denoising Autoencoders.” In: Proceedings of the 25th International Conference on Machine learning. ISBN:978-1-60558-205-4 doi:10.1145/1390156.1390294
Subject Headings: Denoising Auto-Encoder, , Sparse Autoencoder.
Notes
- PowerPoint Presentation: http://www.iro.umontreal.ca/~lisa/seminaires/25-03-2008-2.pdf
Cited By
- Google Scholar: ~ 3,523 Citations
- DL-ACM: ~ 360 Citations
- Semantic Scholar: ~ 2,458 Citations
Quotes
Abstract
Previous work has shown that the difficulties in learning deep generative or discriminative models can be overcome by an initial unsupervised learning step that maps inputs to useful intermediate representations. We introduce and motivate a new training principle for unsupervised learning of a representation based on the idea of making the learned representations robust to partial corruption of the input pattern. This approach can be used to train autoencoders, and these denoising autoencoders can be stacked to initialize deep architectures. The algorithm can be motivated from a manifold learning and information theoretic perspective or from a generative model perspective. Comparative experiments clearly show thesurprising advantage of corrupting the input of autoencoders on a pattern classification benchmark suite.
Appearing in Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 2008. Copyright 2008 by the author(s)/owner(s).
1. Introduction
Recent theoretical studies indicate that deep architectures (Bengio & Le Gun; 2007; Bengio; 2007) may be needed to aficiently model complex distributions and achieve better generalization performance on Challenging recognition tasks. The belief that additional levels of functional composition Will yield increased representational and modeling power is not new (McClelland et a1.; 1986; Hinton; 1989; Utgoff & Stracuzzi; 2002). However; in practice; learning in deep architectures has proven to be difficult. One needs only to ponder the difficult problem of inference in deep directed graphical models; due to “explaining away”. Also looking back at the history of multi—layer neural networks; their difficult optimization (Bengio et a1.; 2007; Bengio; 2007) has long prevented reaping the expected benefits of going beyond one or two hidden layers. However this situation has recently Changed With the successful approach of (Hinton et a1.; 2006; Hinton & Salakhutdinov; 2006; Bengio et al.; 2007; Ranzato et a1.; 2007; Lee et a1.; 2008) for training Deep Belief Networks and stacked autoencoders.
One key ingredient to this success appears to be the use of an unsupervised training criterion to perform a 1ayer—by—1ayer initialization: each layer is at first trained to produce a higher level (hidden) representation of the observed patterns; based on the representation it receives as input from the layer below; by optimizing a local unsupervised criterion. Each level produces a representation of the input pattern that is more abstract than the previous 1eve1’s; because it is obtained by composing more operations. This initialization yields a starting point; from Which a global fine—tuning of the model’s parameters is then performed using another training criterion appropriate for the task at hand. This technique has been shown empirically to avoid getting stuck in the kind of poor solutions one typically reaches With random initializations. While unsupervised learning of a mapping that produces “good” intermediate representations of the input pattern seems to be key; little is understood regarding What constitutes “good” representations for initializing deep architectures; or What explicit criteria n1ay guide learning such representations. We know of only a few algorithms that seem to work well for this purpose: Restricted Boltzmann Machines (RBMs) trained With contrastive divergence on one hand; and various types of autoencoders on the other.
The present research begins With the question of What explicit criteria a good intermediate representation should satisfy. Obviously; it should at a minimum retain a certain amount of “information” about its input; while at the same time being constrained to a given form (e.g. a rea1—va1ued vector of a given size in the case of an autoencoder). A supplemental criterion that has been proposed for such models is sparsity of the representation (Ranzato et a1.; 2008; Lee et a1.; 2008). Here we hypothesize and investigate an additional specific criterion: robustness to partial destruction of the input; i.e.; partially destroyed inputs should yield almost the same representation. It is motivated by the following informal reasoning: a good representation is expected to capture stab1e structures in the form of dependencies and regularities Characteristic of the (unknown) distribution of its observed input. For high dimensional redundant input (such as images) at least; such structures are likely to depend on evidence gathered from a combination of many input dimensions. They should thus be recoverable from partial observation only. A hallmark of this is our human ability to recognize partially occluded or corrupted images. Further evidence is our ability to form a high level concept associated to multiple modalities (such as image and sound) and recall it even when some of the modalities are missing.
To validate our hypothesis and assess its usefulness as one of the guiding principles in learning deep architectures; we propose a modification to the autoencoder framework to explicitly integrate robustness to partially destroyed inputs. Section 2 describes the algorithm in details. Section 3 discusses links with other approaches in the literature. Section 4 is devoted to a Closer inspection of the model from different theoretical standpoints. In section 5 we verify empirically if the algorithm leads to a difference in performance. Section 6 concludes the study.
2. Description of the Algorithm
2.1. Notation and Setup
Let X and Y be two random variables with joint probability density p(X;Y); with marginal distributions p(X) and p(Y). Throughout the text; we will use the following notation: Expectation: IEp(X)[f(X)] : pr) X).dX Entropy: H(X) : IH (p) : Ep(X))f[ ()logp(X)]. Conditional entropy: |H(X1Y) : Ep(X7y)[7 logp(X1Y)]. Kuflback-Leib1er divergence: DKLWIQ) = Ep(x)[10gp W Cross-entropy |H(p1lq)= Ep(X)[7 log q(X)]: H(p ) 7 IDKL(qu). Mutual information: I(X;Y) : |H(X) 7 |H(X1Y). Sigmoid: S(x) : H—ifl and S(X) : (8(X1); . . .;S(Xd))T. Bernoulli distribution with mean M2 BMW).and by extension BM(X) : (BM1(X1)7 ' ' ' 7B,U4d(xd))~
The setup we consider is the typical supervised learning setup with a training set of 71 (input; target) pairs Dn : {(X(1);t(1)) . . . ; (X(n);t(”))}; that we suppose to be an i.i.d. sample from an unknown distribution g(X; T) with corresponding marginals g(X) and g(T).
2.2. The Basic Autoencoder
We begin by recalling the traditional autoencoder model such as the one used in (Bengio et a1.; 2007) to build deep networks. An autoencoder takes an input vector X E [0,11d; and first maps it to a hid— den representation y E [0; 11d, through a deterministic mapping y : fg(X) : S(WX 7 b); parameterized by 6’ : {W;b}. W is a d’ X d weight matrix and b is a bias vector. The resulting 1atent representation y is then mapped back to a “reconstructed” vector 6 [0,11d in input space 2 : ggr(y) : S(W’y 7 b’) with 6” : {W’;b’}. The weight matrix W’ of the reverse mapping may optionally be constrained by W’ : WT; in which case the autoencoder is said to have tied weights. Each training X(i) is thus mapped to a corresponding y(i) and a reconstruction z”). The parameters of this model are optimized to minimize the average reconstruction error.
where L is a loss function such as the traditional squared error L(X; z) : “X 7 2H2. An alternative loss; suggested by the interpretation of X and 2 as either bit vectors or vectors of bit probabilities (Bernou11is) is the reconstruction cross-entropy:
Note that if X is a binary vector; LH(X; z) is a negative log—likelihood for the example X; given the Bernoulli parameters 2. Equation 1 with L : L... can be written
where q0(X) denotes the empirical distribution asso— ciated to our 71 training inputs. This optimization will typically be carried out by stochastic gradient descent.
2.3. The Denoising Autoencoder
To test our hypothesis and enforce robustness to partially destroyed inputs we modify the basic autoencoder we just described. We will now train it to reconstruct a Clean “repaired” input from a corrupted; partially destroyed one. This is done by first corrupting the initial input X to get a partially destroyed version X by means of a stochastic mapping X N qD(X1X). In our experiments; we considered the following corrupting process; parameterized by the desired proportion Z/ of “destruction”: for each input X; a fixed number Z/d of components are Chosen at random; and their value is forced to 0; while the others are left untouched. All information about the Chosen components is thus removed from that particu1er input pattern; and the autoencoder will be trained to “fiH—in” these artificially introduced “blanks”. Note that alternative corrupting noises could be considered[1]. The corrupted input X is then mapped; as with the basic autoencoder; to a hidden representation y : fg(X) : S(WX7b) from which we reconstruct a z : ggr(y) : S(W’y 7 b’) (see figure 1 for a schematic representation of the process). As before the parameters are trained to minimize the average reconstruction error LH(X;z) : IH (BXHBz) over a training set; i.e. to have 2 as Close as possible to the uncorrupted input X. But the key difference is that z is now a deterministic function of X rather than X and thus the result of a stochastic mapping of X.
Let us define the joint distribution
where 6u(v) puts mass 0 when u 7é 1}. Thus Y is a deterministic function of 5?. q0(X;)T;Y) is parameterized by 6’. The objective function minimized by stochastic gradient descent becomes:
So from the point of view of the stochastic gradient descent algorithm; in addition to picking an input sample from the training set; we will also produce a random corrupted version of it; and take a gradient step towards reconstructing the uncorrupted version from the corrupted version. Note that in this way; the autoencoder cannot learn the identity; unlike the basic autoencoder; thus removing the constraint that d’ < d or the need to regularize specifically to avoid such a trivial solution.
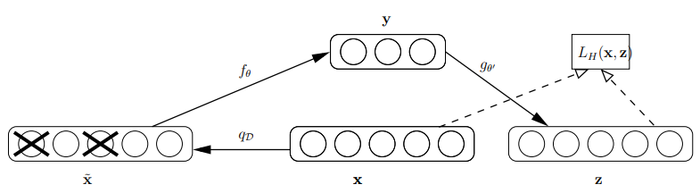
2.4. Layer-wise Initialization and Fine Tuning
The basic autoencoder has been used as a building block to train deep networks (Bengio et a1.; 2007); with the representation of the k-th 1ayer used as input for the (k 7 1)-th; and the (k 7 1)-th 1ayer trained after the k-th has been trained. After a few layers have been trained; the parameters are used as initialization for a network optimized with respect to a supervised training criterion. This greedy 1ayer—wise procedure has been shown to yield significantly better local minima than random initialization of deep networks; achieving better generalization on a number of tasks (Laroche11e et a1.; 2007).
The procedure to train a deep network using the denoising autoencoder is similar. The only difference is how each layer is trained; i.e.; to minimize the criterion in eq. 5 instead of eq. 3. Note that the corruption process qp is only used during training; but not for propagating representations from the raw input to higher-level representations. Note also that when layer k is trained; it receives as input the uncorrupted output of the previous layers.
3. Relationship to Other Approaches
Our training procedure for the denoising autoencoder involves learning to recover a Clean input from a corrupted version; a task known as denoising. The problem of image denoising; in particular; has been extensively studied in the image processing community and many recent developments rely on machine learning approaches (see e.g. Roth and Black (2005); Elad and Aharon (2006); Hammond and Simoncefli (2007)). A particular form of gated autoencoders has also been used for denoising in Memisevic (2007). Denoising using autoencoders was actually introduced much ear1ier (LeCun; 1987; Ga11inari et a1.; 1987); as an alternative to Hopfield models (Hopfield; 1982). Our objective however is fundamentally different from that of developing a competitive image denoising algorithm. We investigate explicit robustness to corrupting noise as a novel criterion guiding the learning of suitable intermediate representations to initialize a deep network. Thus our corruption7denoising procedure is applied not only on the input; but also recursively to intermediate representations.
The approach also bears some resemblance to the well-known technique of augmenting the training data with stochastically “transformed” patterns. E.g. augmenting a training set by transforming original bitmaps through small rotations; translations; and scalings is known to improve final classification performance. In contrast to this technique our approach does not use any prior knowledge of image topology; nor does it produce extra labeled examples for supervised training. We use corrupted patterns in a generic (i.e. not specific to images) unsupervised initialization step; while the supervised training phase uses the unmodified original data.
There is a well-known link between “training with noise” and regularization: they are equivalent for small additive noise (Bishop; 1995). By contrast; our corruption process is a large; non-additive; destruction of information. We train autoencoders to ”fill in the blanks”; not merely be smooth functions (regularization). Also in our experience; regularized autoencoders (i.e. with weight decay) do not yield the quantitative jump in performance and the striking qualitative difference observed in the filters that we get with denoising autoencoders.
There are also similarities with the work of (Doi et al.; 2006) on robust coding over noisy channels. In their framework; a linear encoder is to encode a clean input for optimal transmission over a noisy channel to a decoder that reconstructs the input. This work was later extended to robustness to noise in the input; in a proposal for a model of retinal coding (Doi & Lewicki; 2007). Though some of the inspiration behind our work comes from neural coding and computation; our goal is not to account for experimental data of neuronal activity as in (Doi & Lewicki; 2007). Also; the non—linearity of our denoising autoencoder is crucial for its use in initializing a deep neural network.
It may be objected that; if our goal is to handle missing values correctly; we could have more naturally defined a proper latent variable generative model, and infer the posterior over the latent (hidden) representation in the presence of missing inputs. But this usually requires a costly marginalization[2] which has to be carried out for each new example. By contrast; our approach tries to learn a fast and robust deterministic mapping f9 from examples of already corrupted inputs. The burden is on learning such a constrained mapping during training; rather than on unconstrained inference at use time. We expected this may force the model to capture implicit invariances in the data and result in interesting features. Also, note that in section 4.2 we will see how our learning algorithm for the denoising autoencoder can be viewed as a form of variational inference in a particular generative model.
4. Analysis of Denoising Autoencoders
The above intuitive motivation for the denoising autoencoder was given with the perspective of discovering robust representations. In the following; which can be skipped without hurting the remainder of the paper, we propose alternative perspectives on the algorithm.
4.1. Manifold Learning Perspective
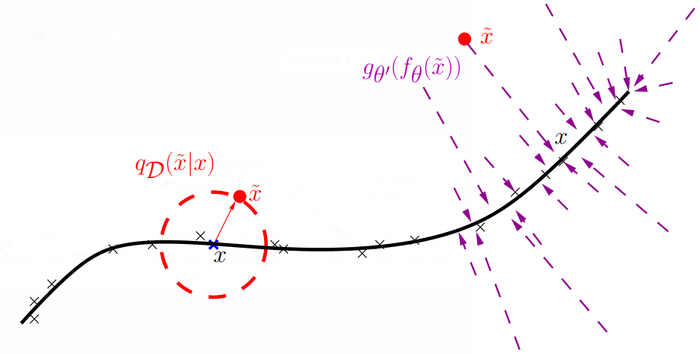
The process of mapping a corrupted example to an uncorrupted one can be visualized in Figure 2; with a low-dimensional manifold near which the data concentrate. We learn a stochastic operator p(XlX) that maps an X to an X; p(XlX) : gg,(f9(X))(X)' The corrupted examples will be much more likely to be outside and farther from the manifold than the uncorrupted ones. Hence the stochastic operator p(XlX) learns a~n1ap that tends to go from lower probability points X to high probability points X; generally on or near the manifold. Note that when X is farther from the manifold; p(XlX) should learn to make bigger steps; to reach the manifold. At the limit we see that the operator should map even far away points to a small volume near the manifold.
The denoising autoencoder can thus be seen as a way to define and learn a manifold. The intermediate representation Y : f(X) can be interpreted as a coordinate system for points on the manifold (this is most clear if we force the dimension of Y to be smaller than the dimension of X). More generally; one can think of Y : f(X) as a representation of X which is well suited to capture the main variations in the data; i.e.; on the manifold. When additional criteria (such as sparsity) are introduced in the learning model; one can no longer directly view Y : f (X ) as an explicit low—din1ensional coordinate system for points on the manifold; but it retains the property of capturing the main factors of variation in the data.
4.2. Top-down, Generative Model Perspective
In this section we recover the training criterion for our denoising autoencoder (eq. 5) from a generative model perspective. Specifically we show that training the denoising autoencoder as described in section 2.3 is equivalent to maximizing a variational bound on a particular generative model.
Consider the generative model p(X;X;Y) p<Y)p<X1Y)p<X1X) where MW) 7 BMW and
p(XlX) : qD(XlX). p(Y) is a uniform prior over Y E [0; 11d]. This defines a generative model with parameter set 6” : {W’;b’}. We will use the previously defined qO(X;X;Y) : qO(X)qD(XlX)6fQ(§)(Y) (equation 4) as an auXiliary model in the context of a variational approximation of the log—likelihood of p(X). Note that we abuse notation to make it lighter; and use the same letters X; X and Y for different sets of random variables representing the same quantity under different distributions: 1) or go. Keep in mind that whereas we had the dependency structure X7>X7>onrqorq0;wehaveY7>X7>Xforp.
Since 1) contains a corruption operation at the last generative stage; we propose to fit p(X) to corrupted training samples. Performing maximum likelihood fitting for samples drawn from qO(X) corresponds to minimizing the cross-entropy; or maximizing
[math]\displaystyle{ ... }[/math] Let q [math]\displaystyle{ .... }[/math] be a conditional density, the quantity [math]\displaystyle{ ... }[/math] is a lower bound on log p(X) since the following can be shown to be true for any q*: [math]\displaystyle{ ... }[/math] Also it is~easy to verifyvthat the bound is tight when q*(X;YlX) : p(X;YlX); where the IDKL becomes 0. We can thus write logp(X) : max? £(q*;X); and consequently rewrite equation 6 as
[math]\displaystyle{ ... }[/math]
where we moved the maximization outside of the eXpectation because an unconstrained q*(X;YlX) can in principle perfectly model the conditional distribution needed to maximize £(q*;X) for any X. Now if we replace the maximization over an unconstrained q* by the maximization over the parameters 6’ of our qO (appearing in f9 that maps an X to a y); we get a lower bound on 'H: 'H 2 maeryg{|Eq0(§)[£(qO;X)]} Maximizing this lower bound; we find
[math]\displaystyle{ [...] }[/math]
Note that 6’ only occurs in Y : fg(X); and 6” only occurs in p(XlY). The last line is therefore obtained because qO (XlX) (X qp (XlX)qO(X) (none of which depends on (6’; 6”)); and q0(YlX) is deterministic; i.e.; its entropy is constant; irrespective of (6,6’). Hence the entropy of q0(X;YlX) : q0(YlX)qO(XlX); does not vary with (6,6”). Finally; following from above; we obtain our training criterion (eq. 5):
[math]\displaystyle{ [...] }[/math]
where the third line is obtained because (6,6”) have no influence on |Eq0(X7)}yy)[logp(Y)] because we chose p(Y) uniform; i.e. constant; nor on Eq0(X §)[logp(XlX)]; and the last line is obtained by inspection of the definition of L... in eq. 2; when
[math]\displaystyle{ [...] }[/math]
4.3. Other Theoretical Perspectives
Information-Theoretic Perspective: Consider [math]\displaystyle{ X \approx q(X) }[/math], [math]\displaystyle{ q }[/math] unknown, [math]\displaystyle{ Y = f_{\theta}(\tilde{X}) }[/math]. It can easily be shown (Vincent et al., 2008) that minimizing the expected reconstruction error amounts to minimizing a lower bound on mutual information [math]\displaystyle{ \mathbf{I}(X; Y) }[/math]. Denoising autoencoders can thus be justified by the objective that [math]\displaystyle{ Y }[/math] captures as much information as possible about [math]\displaystyle{ X }[/math] even as [math]\displaystyle{ Y }[/math] is a function of corrupted input.
Stochastic Operator Perspective: Extending the manifold perspective, the denoising autoencoder can also be seen as corresponding to a semi-parametric model from which we can sample (Vincent et al., 2008):
a where [math]\displaystyle{ \mathbf{x}_i }[/math]; is one of the [math]\displaystyle{ n }[/math] training examples.
5. Experiments
We performed experiments with the proposed algorithm on the same benchmark of classification problems used in (Larochelle et al.; 2007)[3]. It contains different variations of the MNIST digit classification problem (input dimensionality [math]\displaystyle{ d = 28 \times 28 = 784 }[/math]), with added factors of variation such as rotation (rot), addition of a background composed of random pixels (bg-mnd) or made from patches extracted from a set of images (bg-img), or combinations of these factors (rot-bg-img). These variations render the problems particularly challenging for current generic learning algorithms. Each problem is divided into a training, validation; and test set (10000, 2000, 50000 examples respectively). A subset of the original MNIST problem is also included with the same example set sizes (problem basic). The benchmark also contains additional binary classification problems: discriminating between convex and non-convex shapes (convex); and between wide and long rectangles (rect; rect-img).
Neural networks with 3 hidden layers initialized by stacking denoising autoencoders (SdA-3); and fine-tuned on the classification tasks, were evaluated on all the problems in this benchmark. Model selection was conducted following a similar procedure as Larochelle et al. (2007). Several values of hyperparameters (destruction fraction [math]\displaystyle{ \nu }[/math] layer sizes; number of unsupervised training epochs) were tried; combined with early stopping in the fine-tuning phase. For each task; the best model was selected based on its classification performance on the validation set.
Table 1 reports the resulting classification error on the test set for the new model (SdA-3); together with the performance reported in Larochelle et al. (2007) [4] for SVMs with Gaussian and polynomial kernels; 1 and 3 hidden layers deep belief network (DBN-1 and DBN-3) and a 3 hidden layer deep network initialized by stacking basic autoencoders (SAA-3). Note that SAA-3 is equivalent to a SdA—3 with [math]\displaystyle{ \nu = 0% }[/math] destruction. As can be seen in the table, the corruption+denoising training works remarkably well as an initialization step; and in most cases yields significantly better classification performance than basic autoencoder stacking with no noise. On all but one task the SdA-3 algorithm performs on par or better than the best other algorithms, including deep belief nets. Due to space constraints, we do not report all selected hyperparameters in the table (only showing [math]\displaystyle{ \nu }[/math])]]. But it is worth mentioning that, for the majority of tasks; the model selection procedure chose best performing models with an overcomplete first hidden layer representation (typically of size 2000 for the 784-dimensional MNIST-derived tasks). This is very different from the traditional “bottleneck” autoencoders; and made possible by our denoising training procedure. All this suggests that the proposed procedure was indeed able to produce more useful feature detectors.
Next, we wanted to understand qualitatively the effect of the corruption+denoising training. To this end we display the filters obtained after initial training of the first denoising autoencoder on MNIST digits. Figure 3 shows a few of these filters as little image patches, for different noise levels. Each patch corresponds to a row of the learnt weight matrix [math]\displaystyle{ \mathbf{W} }[/math], i.e. the incoming weights of one of the hidden layer neurons. The beneficial effect of the denoising training can clearly be seen. Without the denoising procedure, many filters appear to have learnt no interesting feature. They look like the filters obtained after random initialization. But when increasing the level of destructive corruption, an increasing number of filters resemble sensible feature detectors. As we move to higher noise levels, we observe a phenomenon that we expected: filters become less local, they appear sensitive to larger structures spread out across more input dimensions.
| Dataset | SVMWrbf | SVMpoly | DBN-1 | SAA-3 | DBN-3 | SdA-3 [math]\displaystyle{ (\nu) }[/math] |
|---|---|---|---|---|---|---|
| basic | 3.03 ±0.15 | 3.69±0.17 | 3.94±0.17 | 3.46±0.16 | 3.11±0.15 | 2.80±0.14 (10%) |
| rot | 11.11±0.28 | 15.42±0.32 | 14.69±0.31 | 10.30±0.27 | 10.30±0.27 | 10.29±0.27 (10%) |
| bg-mnd | 14.58±0.31 | 16.62±0.33 | 9.80±0.26 | 11.28±0.28 | 6.73±0.22 | 10.38±0.27 (40%) |
| bg-img | 22.61±0.37 | 24.01±0.37 | 16.15±0.32 | 23.00±0.37 | 16.31±0.32 | 16.68±0.33 (25%) |
| rot-bg-img | 55.18±0.44 | 56.41±0.43 | 52.21±0.44 | 51.93±0.44 | 47.39±0.44 | 44.49±0.44 (25%) |
| rect | 2.15±0.13 | 2.15±0.13 | 4.71±0.19 | 2.41±0.13 | 2.60±0.14 | 1.99±0.12 (10%) |
| rect-img | 24.04±0.37 | 24.05±0.37 | 23.69±0.37 | 24.05±0.37 | 22.50±0.37 | 21.59±0.36 (25%) |
| conver | 19.13±0.34 | 19.82±0.35 | 19.92±0.35 | 18.41±0.34 | 18.631034 | 19.06±0.34 (10%) |

(a—c) show some of the filters obtained after training a denoising autoencoder on MNIST samples, with increasing destruction levels [math]\displaystyle{ \nu }[/math]. The filters at the same position in the three images are related only by the fact that the autoencoders were started from the same random initialization point.
(d) and (e) zoom in on the filters obtained for two of the neurons, again for increasing destruction levels. As can be seen, with no noise, many filters remain similarly uninteresting (undistinctive almost uniform grey patches). As we increase the noise level, denoising training forces the filters to differentiate more, and capture more distinctive features. Higher noise levels tend to induce less local filters, as expected. One can distinguish different kinds of filters, from local blob detectors, to stroke detectors, and some full character detectors at the higher noise levels.
6. Conclusion and Future Work
We have introduced a very simple training principle for autoencoders; based on the objective of undoing a corruption process. This is motivated by the goal of learning representations of the input that are robust to small irrelevant changes in input. We also motivated it from a manifold learning perspective and gave an interpretation from a generative model perspective.
This principle can be used to train and stack autoencoders to initialize a deep neural network. A series of image classification experiments were performed to evaluate this new training principle. The empirical results support the following conclusions: unsupervised initialization of layers with an explicit denoising criterion helps to capture interesting structure in the input distribution. This in turn leads to intermediate representations much better suited for subsequent learning tasks such as supervised classification. It is possible that the rather good experimental performance of Deep Belief Networks (whose layers are initialized as RBMs) is partly due to RBMs encapsulating a similar form of robustness to corruption in the representations they learn, possibly because of their stochastic nature which introduces noise in the representation during training. Future work inspired by this observation should investigate other types of corruption process, not only of the input but of the representation itself as well.
Acknowledgments
We thank the anonymous reviewers for their useful comments that helped improve the paper. We are also very grateful for the financial support of this work by NSERC, MITACS, and CIFAR.
Footnotes
- ↑ The approach we describe and our analysis is not specific to a particular kind of corrupting noise.
- ↑ as for RBMS, where it is exponential in the number of missing values
- ↑ All the datasets for these problems are available at http://www.iro.umontreal.ca/~lisa/icrnl2007.
- ↑ Except that rot and rot-bg-img, as reported on the website from which they are available, have been regenerated since Larochelle et al. (2007), to fix a problem in the initial data generation process. We used the updated data and corresponding benchmark results given on this website.
References
;
| Author | volume | Date Value | title | type | journal | titleUrl | doi | note | year | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2008 ExtractingandComposingRobustFea | Yoshua Bengio Pierre-Antoine Manzagol Pascal Vincent Hugo Larochelle | Extracting and Composing Robust Features with Denoising Autoencoders | 10.1145/1390156.1390294 | 2008 |