Markov Blanket
A Markov Blanket of a Directed Graph Graph Node are its Parent Nodes, Children Nodes, and the Parent Node of the Children Nodes.
- Example(s):
- Counter-Example(s):
- See: Markov Chain, Markov Property, Markov Random Field, Bayesian Network Estimation, Metropolis-Hastings Algorithm, MCMC Simulation, Gibbs Sampler, Gaussian Graphical Model.
References
2018
- (Wikipedia, 2018) ⇒ https://en.wikipedia.org/wiki/Markov_blanket Retrieved:2018-11-14.
- In statistics and machine learning, the Markov blanket for a node in a graphical model contains all the variables that shield the node from the rest of the network. This means that the Markov blanket of a node is the only knowledge needed to predict the behavior of that node and its children. The term was coined by Judea Pearl in 1988.
In a Bayesian network, the values of the parents and children of a node evidently give information about that node. However, its children's parents also have to be included, because they can be used to explain away the node in question. In a Markov random field, the Markov blanket for a node is simply its adjacent nodes.
The Markov blanket for a node [math]\displaystyle{ A }[/math] in a Bayesian network is the set of nodes [math]\displaystyle{ \partial A }[/math] composed of [math]\displaystyle{ A }[/math] 's parents, its children, and its children's other parents. In a Markov random field, the Markov blanket of a node is its set of neighboring nodes. The Markov blanket of A may also be denoted by [math]\displaystyle{ \operatorname{MB}(A) }[/math] .
Every set of nodes in the network is conditionally independent of [math]\displaystyle{ A }[/math] when conditioned on the set [math]\displaystyle{ \partial A }[/math], that is, when conditioned on the Markov blanket of the node [math]\displaystyle{ A }[/math] . The probability has the Markov property; formally, for distinct nodes [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] :
[math]\displaystyle{ \Pr(A \mid \partial A , B) = \Pr(A \mid \partial A). \! }[/math]
- In statistics and machine learning, the Markov blanket for a node in a graphical model contains all the variables that shield the node from the rest of the network. This means that the Markov blanket of a node is the only knowledge needed to predict the behavior of that node and its children. The term was coined by Judea Pearl in 1988.
2015
- (Kaufmann et al., 2015) ⇒ Dinu Kaufmann, Sonali Parbhoo, Aleksander Wieczorek, Sebastian Keller, David Adametz, and Volker Roth. (2015). “Bayesian Markov Blanket Estimation.” arXiv:1510.01485.
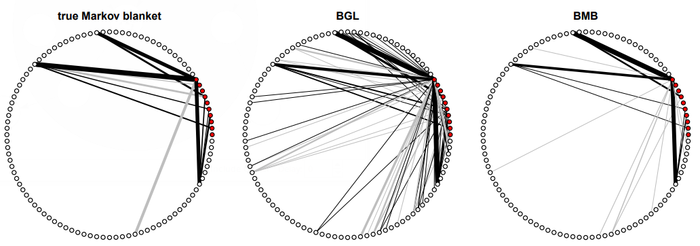
- QUOTE: Fig. 2 depicts a true Markov blanket and its reconstruction by BGL and BMB using the same sparsity parameter [math]\displaystyle{ \lambda = 200 }[/math]. Both methods were run side-by-side for 700 MCMC samples after an initial burn-in phase of 300 samples. From the sampled networks, a representative network structure is constructed by thresholding based on a 85% credibility interval. We repeat the above procedure to obtain a total of 100 datasets. The quality of reconstructed networks is measured in terms of f-score (harmonic mean of precision and recall) between the true and inferred Markov blanket.
Figure 2: One exemplary Markov blanket [math]\displaystyle{ (p = 10, q = 90) }[/math] and its reconstruction by BGL and BMB. Note that the graphs only display edges between [math]\displaystyle{ p }[/math] query and [math]\displaystyle{ q }[/math] remaining variables. Red nodes represent query variables, white nodes represent all other variables. Black and grey edges correspond to positive and negative edge signs, respectively.
When computing precision and recall, inferred edges with edge weights having the wrong sign are counted as missing. Both models share the same sparsity parameter [math]\displaystyle{ \lambda }[/math], which in this experiment was selected such that for BMB recall and precision have roughly the same value.
- QUOTE: Fig. 2 depicts a true Markov blanket and its reconstruction by BGL and BMB using the same sparsity parameter [math]\displaystyle{ \lambda = 200 }[/math]. Both methods were run side-by-side for 700 MCMC samples after an initial burn-in phase of 300 samples. From the sampled networks, a representative network structure is constructed by thresholding based on a 85% credibility interval. We repeat the above procedure to obtain a total of 100 datasets. The quality of reconstructed networks is measured in terms of f-score (harmonic mean of precision and recall) between the true and inferred Markov blanket.
2006
- (Kulaga, 2006) ⇒ Tomasz Kulaga. (2006). "The Markov Blanket Concept in Bayesian Networks and Dynamic Bayesian Networks and Convergence Assessment in Graphical Model Selection Problems". Master Thesis. Jagiellonian University. Chapter4: "Markov Blanket".
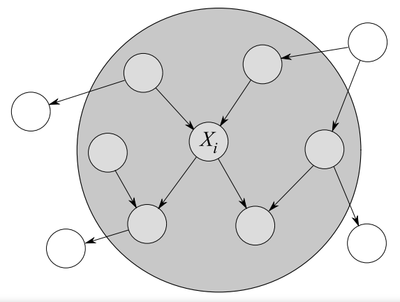
- QUOTE: Formally the definition of Markov Blanket in a BN, or more general in a graph, is as follows.
[math]\displaystyle{ MB(X_i) = Par(X_i) \cup Ch(Xi) \cup \underset{Y \in Ch(X_i)}{\cup} Par(Y) }[/math]
Let us see this on an example.
Figure 4.1: Example of Markov Blanket for node [math]\displaystyle{ X_i }[/math].
- QUOTE: Formally the definition of Markov Blanket in a BN, or more general in a graph, is as follows.
2003
- (Korb & Nicholson, 2003) ⇒ Kevin B. Korb, and Ann E. Nicholson. (2003). “Bayesian Artificial Intelligence." Chapman & Hall/CRC.
- Another useful concept is that of the Markov Blanket of a node, which consists of the node's parents, its children and its children's parents.
2023
- (Wikipedia, 2023) ⇒ https://en.wikipedia.org/wiki/Markov_blanket Retrieved:2023-10-9.
- In statistics and machine learning, when one wants to infer a random variable with a set of variables, usually a subset is enough, and other variables are useless. Such a subset that contains all the useful information is called a Markov blanket. If a Markov blanket is minimal, meaning that it cannot drop any variable without losing information, it is called a Markov boundary. Identifying a Markov blanket or a Markov boundary helps to extract useful features. The terms of Markov blanket and Markov boundary were coined by Judea Pearl in 1988. A Markov blanket can be constituted by a set of Markov chains.