Partially Observable Markov Decision Process (POMDP)
A Partially Observable Markov Decision Process (POMDP) is a Markov decision process that is also a partially observable environment.
- AKA: Belief State Markov Decision Process, Dual Control, Dynamic Decision Network.
- Context:
- It can be represented by a 5-tuple [math]\displaystyle{ (S,A,O,T,\Omega,R) }[/math], such that:
- [math]\displaystyle{ S }[/math] is a set of states,
- [math]\displaystyle{ A }[/math] is a set of actions,
- [math]\displaystyle{ O }[/math] is a set of observations,
- [math]\displaystyle{ T }[/math] is a set of conditional transition probabilities,
- [math]\displaystyle{ \Omega }[/math] is a set of conditional observation probabilities,
- [math]\displaystyle{ R: A,S \to \mathbb{R} }[/math] is the reward function.
- It can have a Belief State that is a probability distribution over states.
- It can have a Belief Space that is the entire probability space, infinite.
- It can be graphically represented as an Influence Diagram.
- It can be represented by a 5-tuple [math]\displaystyle{ (S,A,O,T,\Omega,R) }[/math], such that:
- Example(s):
- a Factored POMDP (Boutilier & Poole 1996);
- a Continuous POMDP (Porta et al. 2006);
- a Hierarchical POMDP (Theocharous & Mahadevan 2002, Pineau et al. 2003, and Toussaint et al. 2008);
- a Reinforcement Learning POMDP (Meuleau et al. 1999, and Aberdeen & Baxter 2002);
- a Bayes Adaptive POMDP (Ross et al. 2007; Poupart & Vlassis 2008);
- an Aggregated POMDP (Shani et al. 2008; Sim et al. 2008);
- a Compressed POMPDP (Poupart & Boutilier 2004, Roy et al. 2005);
- a Decentralized POMDP (Amato et al. 2009);
- an Interactive POMDP (Gmytrasiewicz & Doshi 2005);
- …
- Counter-Example(s):
- See: Sequential Decision-Making, Discrete-State Model, Discrete-Time Model, Automated Planning, Q-Learning.
References
2017a
- (Wikipedia, 2017) ⇒ https://en.wikipedia.org/wiki/Partially_observable_Markov_decision_process Retrieved:2017-6-14.
- A partially observable Markov decision process (POMDP) is a generalization of a Markov decision process (MDP). A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot directly observe the underlying state. Instead, it must maintain a probability distribution over the set of possible states, based on a set of observations and observation probabilities, and the underlying MDP.
The POMDP framework is general enough to model a variety of real-world sequential decision processes. Applications include robot navigation problems, machine maintenance, and planning under uncertainty in general. The framework originated in the operations research community, and was later adapted by the artificial intelligence and automated planning communities.
An exact solution to a POMDP yields the optimal action for each possible belief over the world states. The optimal action maximizes (or minimizes) the expected reward (or cost) of the agent over a possibly infinite horizon. The sequence of optimal actions is known as the optimal policy of the agent for interacting with its environment.
- A partially observable Markov decision process (POMDP) is a generalization of a Markov decision process (MDP). A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot directly observe the underlying state. Instead, it must maintain a probability distribution over the set of possible states, based on a set of observations and observation probabilities, and the underlying MDP.
2017b
- (Poupart, 2017) ⇒ Pascal Poupart. (2017). “Partially Observable Markov Decision Processes”. In: (Sammut & Webb, 2017). DOI:10.1007/978-1-4899-7687-1_629.
- QUOTE: A partially observable Markov decision process (POMDP) refers to a class of sequential decision-making problems under uncertainty. This class includes problems with partially observable states and uncertain action effects. A POMDP is formally defined by a tuple [math]\displaystyle{ (\mathcal{S}, \mathcal{A}, \mathcal{O}, T,Z, R, b_0,h,\gamma) }[/math] where [math]\displaystyle{ (\mathcal{S} }[/math] is the set of states [math]\displaystyle{ s }[/math]; [math]\displaystyle{ \mathcal{A} }[/math] is the set of actions [math]\displaystyle{ a }[/math]; [math]\displaystyle{ \mathcal{O} }[/math] is the set observations [math]\displaystyle{ o }[/math], [math]\displaystyle{ T(s, a, s') = Pr(s'|s,a) }[/math] is the transition function indicating the probability of reaching [math]\displaystyle{ s' }[/math] when executing [math]\displaystyle{ a }[/math] in [math]\displaystyle{ s }[/math], [math]\displaystyle{ Z(a, s', o') = Pr(o'| a, s') }[/math] is the observation function indicating the probability of observing [math]\displaystyle{ o' }[/math] in state [math]\displaystyle{ s' }[/math] after executing [math]\displaystyle{ a }[/math], [math]\displaystyle{ R(s, a) \in \R }[/math] is the reward function indicating the (immediate) expected utility of executing [math]\displaystyle{ a }[/math] in [math]\displaystyle{ s }[/math], [math]\displaystyle{ b_0 = Pr(s_0) }[/math] is the distribution over the initial state (also known as initial belief), [math]\displaystyle{ h }[/math] is the planning horizon (which may be finite or infinite), and [math]\displaystyle{ \gamma \in [0, 1] }[/math] is a discount factor indicating by how much rewards should be discounted at each time step. Given a POMDP, the goal is to find a policy to select actions that maximize rewards over the planning horizon.
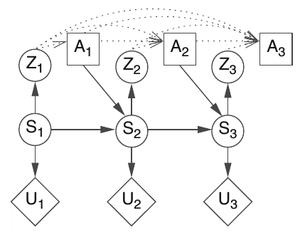
(...) Figure 1 shows the graphical representation of a POMDP, using the notation of influence diagrams: circles denote random variables (e.g., state variables [math]\displaystyle{ S_t }[/math] and observation variables [math]\displaystyle{ O_t }[/math] ), squares denote decision variables (e.g., action variables [math]\displaystyle{ A_t }[/math] ), and diamonds denote utility variables (e.g., [math]\displaystyle{ U_t }[/math] ’s).
- QUOTE: A partially observable Markov decision process (POMDP) refers to a class of sequential decision-making problems under uncertainty. This class includes problems with partially observable states and uncertain action effects. A POMDP is formally defined by a tuple [math]\displaystyle{ (\mathcal{S}, \mathcal{A}, \mathcal{O}, T,Z, R, b_0,h,\gamma) }[/math] where [math]\displaystyle{ (\mathcal{S} }[/math] is the set of states [math]\displaystyle{ s }[/math]; [math]\displaystyle{ \mathcal{A} }[/math] is the set of actions [math]\displaystyle{ a }[/math]; [math]\displaystyle{ \mathcal{O} }[/math] is the set observations [math]\displaystyle{ o }[/math], [math]\displaystyle{ T(s, a, s') = Pr(s'|s,a) }[/math] is the transition function indicating the probability of reaching [math]\displaystyle{ s' }[/math] when executing [math]\displaystyle{ a }[/math] in [math]\displaystyle{ s }[/math], [math]\displaystyle{ Z(a, s', o') = Pr(o'| a, s') }[/math] is the observation function indicating the probability of observing [math]\displaystyle{ o' }[/math] in state [math]\displaystyle{ s' }[/math] after executing [math]\displaystyle{ a }[/math], [math]\displaystyle{ R(s, a) \in \R }[/math] is the reward function indicating the (immediate) expected utility of executing [math]\displaystyle{ a }[/math] in [math]\displaystyle{ s }[/math], [math]\displaystyle{ b_0 = Pr(s_0) }[/math] is the distribution over the initial state (also known as initial belief), [math]\displaystyle{ h }[/math] is the planning horizon (which may be finite or infinite), and [math]\displaystyle{ \gamma \in [0, 1] }[/math] is a discount factor indicating by how much rewards should be discounted at each time step. Given a POMDP, the goal is to find a policy to select actions that maximize rewards over the planning horizon.
2012a
- (Wikipedia, 2012) ⇒ http://en.wikipedia.org/wiki/Partially_observable_Markov_decision_process
- A Partially Observable Markov Decision Process (POMDP) is a generalization of a Markov Decision Process. A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot directly observe the underlying state. Instead, it must maintain a probability distribution over the set of possible states, based on a set of observations and observation probabilities, and the underlying MDP.
The POMDP framework is general enough to model a variety of real-world sequential decision processes. Applications include robot navigation problems, machine maintenance, and planning under uncertainty in general. The framework originated in the Operations Research community, and was later taken over by the Artificial Intelligence and Automated Planning communities.
An exact solution to a POMDP yields the optimal action for each possible belief over the world states. The optimal action maximizes (or minimizes) the expected reward (or cost) of the agent over a possibly infinite horizon. The sequence of optimal actions is known as the optimal policy of the agent for interacting with its environment.
- A Partially Observable Markov Decision Process (POMDP) is a generalization of a Markov Decision Process. A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot directly observe the underlying state. Instead, it must maintain a probability distribution over the set of possible states, based on a set of observations and observation probabilities, and the underlying MDP.
2012b
- (Wikipedia, 2012) ⇒ http://en.wikipedia.org/wiki/Partially_observable_Markov_decision_process#Formal_definition
- A discrete-time POMDP models the relationship between an agent and its environment. Formally, a POMDP is a tuple [math]\displaystyle{ (S,A,O,T,\Omega,R) }[/math], where
- [math]\displaystyle{ S }[/math] is a set of states,
- [math]\displaystyle{ A }[/math] is a set of actions,
- [math]\displaystyle{ O }[/math] is a set of observations,
- [math]\displaystyle{ T }[/math] is a set of conditional transition probabilities,
- [math]\displaystyle{ \Omega }[/math] is a set of conditional observation probabilities,
- [math]\displaystyle{ R: A,S \to \mathbb{R} }[/math] is the reward function.
- At each time period, the environment is in some state [math]\displaystyle{ s \in S }[/math]. The agent takes an action [math]\displaystyle{ a \in A }[/math],
- A discrete-time POMDP models the relationship between an agent and its environment. Formally, a POMDP is a tuple [math]\displaystyle{ (S,A,O,T,\Omega,R) }[/math], where
which causes the environment to transition to state [math]\displaystyle{ s' }[/math] with probability [math]\displaystyle{ T(s'\mid s,a) }[/math]. Finally, the agent receives a reward with expected value, say [math]\displaystyle{ r }[/math], and the process repeats.
2007
- (Williams & Young, 2007) ⇒ Jason D. Williams, and Steve Young. (2007). “Partially Observable Markov Decision Processes for Spoken Dialog Systems.” In: Computer Speech and Language Journal, 21(2). doi:10.1016/j.csl.2006.06.008
- QUOTE: In a spoken dialog system, determining which action a machine should take in a given situation is a difficult problem because automatic speech recognition is unreliable and hence the state of the conversation can never be known with certainty. … In this paper we cast a spoken dialog system as a partially observable Markov decision process (POMDP).
2004
- (Cassandra, 2004) ⇒ http://www.cassandra.org/pomdp/pomdp-faq.shtml
- QUOTE: What is a POMDP? POMDP is an acronym for a partially observable Markov decision process. This is a mathematical model that can capture the domain dynamics that include uncertainty in action effects, uncertainty in perceptual stimuli. Once a problem is captured as POMDP, it them becomes more ammendable for solution using optimization techniques.
Does this have anything to do with Markov Chains or HMMs? Sure does. These are all stochastic, discrete state, discrete time models. Borrowing from Michael Littman's nifty explanatory grid:
- QUOTE: What is a POMDP? POMDP is an acronym for a partially observable Markov decision process. This is a mathematical model that can capture the domain dynamics that include uncertainty in action effects, uncertainty in perceptual stimuli. Once a problem is captured as POMDP, it them becomes more ammendable for solution using optimization techniques.
| Markov Models |
Do we have control over the state transitons? |
||
|---|---|---|---|
| NO | YES | ||
| Are the states completely observable? |
YES | Markov Chain |
MDPMarkov Decision Process |
| NO | HMMHidden Markov Model |
POMDPPartially ObservableMarkov Decision Process |
|
2000
- (Hauskrecht, 2000) ⇒ Milos Hauskrecht. (2000). “Value-function Approximations for Partially Observable Markov Decision Processes.” In: Journal of Artificial Intelligence Research, 13(1).
- QUOTE: Partially observable Markov decision processes (POMDPs) provide an elegant mathematical framework for modeling complex decision and planning problems in stochastic domains in which states of the system are observable only indirectly, via a set of imperfect or noisy observations.