Cross-Validation Algorithm
A cross-validation algorithm is a resampling-based predictor evaluation algorithm that is used for determining whether a statistical analysis will generalize to an independent data set.
- AKA: Rotation Estimation Algorithm, Out-of-Sample Testing Algorithm.
- Context:
- input: threshold, [math]\displaystyle{ n }[/math].
- pseudo-code:
- Segment the Learning Records into [math]\displaystyle{ n }[/math] nearly equally sized sets (Folds) (F1...Fn).
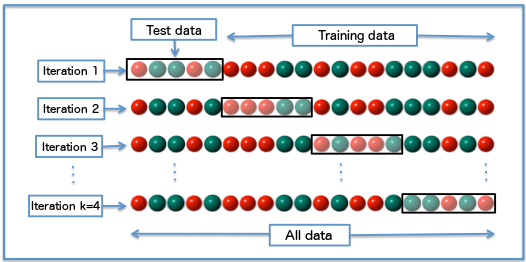
- Run [math]\displaystyle{ n }[/math] Experiments, each using Fi as a Test Set and the other n-1 Folds appended together to form the Train Set.
- Calculate Predictive Model Performance for some desired prediction performance metric (e.g. accuracy) achieved over the [math]\displaystyle{ n }[/math] runs.
- It can be implemented by a cross-validation system to solve a cross-validation task (which requires sampling without replacement to split evaluation data into similar sizes).
- It can range from being a k-Fold Cross-Validation Algorithm (such as 10-fold cross-validation algorithm) to being a Leave-K-Out Cross-Validation Algorithm (such as a leave-one-out cross-validation algorithm).
- It can range from being a Stratified Cross-Validation Algorithm to being an Unstratified Cross-Validation Algorithm.
- It can achieve different levels of Confidence in the Estimate based on the size of n.
- Example(s):
- on Real-World Data (Kohavi, 1995))
- a .632+Bootstrap Validation Algorithm (Efron & Tibshirani, 1997).
- …
- Counter-Example(s):
- See: Predicted Residual Sum of Squares, Model Validation, Accuracy, Partition of a Set, Statistical Sample, Variance Estimation, Hypothesis Testing, Type III Error, Type I and Type II Errors.
References
2023
- (Wikipedia, 2023) ⇒ https://en.wikipedia.org/wiki/Cross-validation_(statistics) Retrieved:2023-1-15.
- Cross-validation, sometimes called rotation estimation[1] [2] or out-of-sample testing, is any of various similar model validation techniques for assessing how the results of a statistical analysis will generalize to an independent data set. Cross-validation is a resampling method that uses different portions of the data to test and train a model on different iterations. It is mainly used in settings where the goal is prediction, and one wants to estimate how accurately a predictive model will perform in practice. In a prediction problem, a model is usually given a dataset of known data on which training is run (training dataset), and a dataset of unknown data (or first seen data) against which the model is tested (called the validation dataset or testing set). [3] The goal of cross-validation is to test the model's ability to predict new data that was not used in estimating it, in order to flag problems like overfitting or selection bias and to give an insight on how the model will generalize to an independent dataset (i.e., an unknown dataset, for instance from a real problem).
One round of cross-validation involves partitioning a sample of data into complementary subsets, performing the analysis on one subset (called the training set), and validating the analysis on the other subset (called the validation set or testing set). To reduce variability, in most methods multiple rounds of cross-validation are performed using different partitions, and the validation results are combined (e.g. averaged) over the rounds to give an estimate of the model's predictive performance.
In summary, cross-validation combines (averages) measures of fitness in prediction to derive a more accurate estimate of model prediction performance.[4]
- Cross-validation, sometimes called rotation estimation[1] [2] or out-of-sample testing, is any of various similar model validation techniques for assessing how the results of a statistical analysis will generalize to an independent data set. Cross-validation is a resampling method that uses different portions of the data to test and train a model on different iterations. It is mainly used in settings where the goal is prediction, and one wants to estimate how accurately a predictive model will perform in practice. In a prediction problem, a model is usually given a dataset of known data on which training is run (training dataset), and a dataset of unknown data (or first seen data) against which the model is tested (called the validation dataset or testing set). [3] The goal of cross-validation is to test the model's ability to predict new data that was not used in estimating it, in order to flag problems like overfitting or selection bias and to give an insight on how the model will generalize to an independent dataset (i.e., an unknown dataset, for instance from a real problem).
- ↑ ohavi, Ron (1995). “A study of cross-validation and bootstrap for accuracy estimation and model selection". Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence. San Mateo, CA: Morgan Kaufmann. 2 (12): 1137–1143. [ohavi, Ron (1995). “A study of cross-validation and bootstrap for accuracy estimation and model selection". Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence. San Mateo, CA: Morgan Kaufmann. 2 (12): 1137–1143. CiteSeerX 10.1.1.48.529 CiteSeerX 10.1.1.48.529]
- ↑ Devijver, Pierre A.; Kittler, Josef (1982). Pattern Recognition: A Statistical Approach. London, GB: Prentice-Hall. ISBN 0-13-654236-0.
- ↑ "Newbie question: Confused about train, validation and test data!". Archived from the original on 2015-03-14. Retrieved 2013-11-14.
- ↑ Grossman, Robert; Seni, Giovanni; Elder, John; Agarwal, Nitin; Liu, Huan (2010). “Ensemble Methods in Data Mining: Improving Accuracy Through Combining Predictions". Synthesis Lectures on Data Mining and Knowledge Discovery. Morgan & Claypool. 2: 1–126. doi:10.2200/S00240ED1V01Y200912DMK002
2011
- (Sammut & Webb, 2011) ⇒ Claude Sammut (editor), and Geoffrey I. Webb (editor). (2011). “Cross-Validation.” In: (Sammut & Webb, 2011) p.306
- Definition: Cross-validation is a process for creating a distribution of pairs of training and test sets out of single data set. In cross validation the data are partitioned into [math]\displaystyle{ k }[/math] subsets, [math]\displaystyle{ S_1,\cdots, S_k }[/math] , each called a fold. The folds are usually of approximately the same size. The learning algorithm is then applied [math]\displaystyle{ k }[/math] times, for [math]\displaystyle{ i=1 }[/math] to [math]\displaystyle{ k }[/math], each time using the union of all subsets other than [math]\displaystyle{ S_i }[/math] as the training set and using [math]\displaystyle{ S_i }[/math] as the test set.
1998
- (Kohavi & Provost, 1998) ⇒ Ron Kohavi, and Foster Provost. (1998). “Glossary of Terms.” In: Machine Leanring 30(2-3).
- QUOTE: Cross-validation: A method for estimating the accuracy (or error) of an inducer by dividing the data into k mutually exclusive subsets (the “folds) of approximately equal size. The inducer is trained and tested k times. Each time it is trained on the data set minus a fold and tested on that fold. The accuracy estimate is the average accuracy for the k folds.
1995
- (Kohavi, 1995) ⇒ Ron Kohavi. (1995). “A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection.” In: Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence (IJCAI 1995).
- QUOTE: We review accuracy estimation methods and compare the two most common methods: cross-validation and bootstrap.
1993
- (Geisser, 1993) ⇒ Seymour Geisser. (1993). “Predictive Inference. Chapman and Hall. ISBN 0412034719.
- Cross-validation: Divide the sample in half, use the second half to "validate" the first half and vice versa, yielding a second validation or comparison. The two may be combined into a single one.
1983
- (Efron & Gong, 1983) ⇒ Bradley Efron and Gail Gong. (1983). “A Leisurely Look at the Bootstrap, the Jackknife, and Cross-Validation.” In: The American Statistician, 37(1). http://www.jstor.org/stable/2685844
- Abstract: This is an invited expository article for The American Statistician. It reviews the nonparametric estimation of statistical error, mainly the bias and standard error of an estimator, or the error rate of a prediction rule. The presentation is written at a relaxed mathematical level, omitting most proofs, regularity conditions, and technical details.