Neural Network Hidden Layer
A Neural Network Hidden Layer is a neural network layer in between the Neural Network Input Layer and the Neural Network Output Layer.
- Context:
- It is composed by Hidden Neuron that are determined by a activation function and a weight funtions.
- It can have a Hidden Layer State that represents a learned combination of input features (see: kernel learning).
- It can range from being a Linear Hidden Layer to being a Non-Linear Hidden Layer.
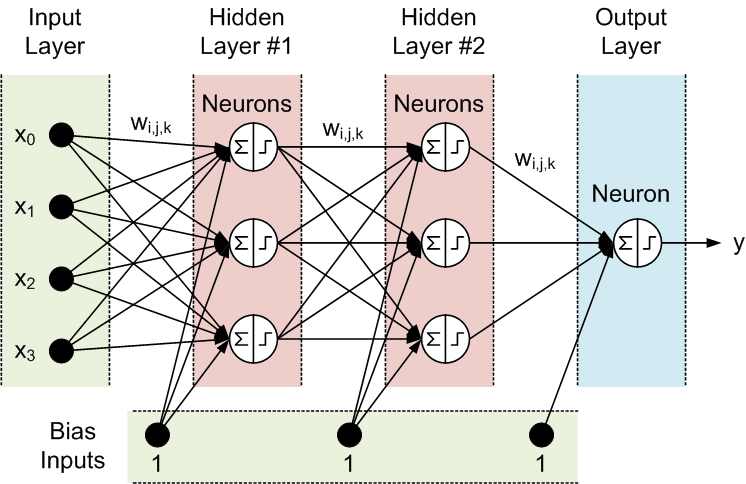
- It can be defined mathematically by as set of artificial neurons [math]\displaystyle{ \{a_0^{(m)}, a_1^{(m)}, \cdots, a_p^{(m)}\} }[/math] in which the j-th neuron is given by
[math]\displaystyle{ a_j^{(m)}=\sum_{j=0}^{p}\sum_{i=0}^n G(w^{(m, m-1)}_{ji}*a_i^{(m-1)}) +b^{(m)} }[/math]
where [math]\displaystyle{ m }[/math] layer is the index number; [math]\displaystyle{ G }[/math] is the hidden layer's activation function; [math]\displaystyle{ w_{ji}^{(m, m-1)} }[/math] are weights between the current layer [math]\displaystyle{ m }[/math] and previous layer [math]\displaystyle{ m-1 }[/math] ; [math]\displaystyle{ b^{(m)} }[/math] is the bias, [math]\displaystyle{ a^{m-1}_i }[/math] are the previous layer neurons.
- Example(s):
- with
- [math]\displaystyle{ a^{(2)}_1 =g(\theta^{(1)}_{10} x_0+\theta^{(1)}_{11} x_1+\theta^{(1)}_{12} x_2+\theta^{(1)}_{13} x_3) }[/math]
- [math]\displaystyle{ a^{(2)}_2 =g(\theta^{(1)}_{20} x_0+\theta^{(1)}_{21} x_1+\theta^{(1)}_{22} x_2+\theta^{(1)}_{23} x_3) }[/math]
- [math]\displaystyle{ a^{(2)}_3 =g(\theta^{(1)}_{30} x_0+\theta^{(1)}_{31} x_1+\theta^{(1)}_{32} x_2+\theta^{(1)}_{33} x_3) }[/math]
- [math]\displaystyle{ h_{\theta}(x)=a^{(3)}_1 =g(\theta^{(2)}_{10} a^{(2)}_0 +\theta^{(2)}_{11} a^{(2)}_1 +\theta^{(2)}_{12} a^{(2)}_2 +\theta^{(2)}_{13} a^{(2)}_3 ) }[/math]
- with
- Counter-Example(s):
- See: Artificial Neural Network, Artificial Neuron, Fully-Connected Neural Network Layer, Neuron Activation Function, Neural Network Weight, Neural Network Connection, Neural Network Topology, Multi Hidden Layer NNet.
References
2017a
- (CS231n, 2017) ⇒ http://cs231n.github.io/neural-networks-1/#layers Retrieved: 2017-12-31
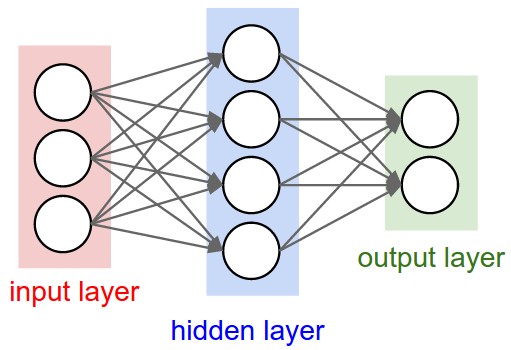
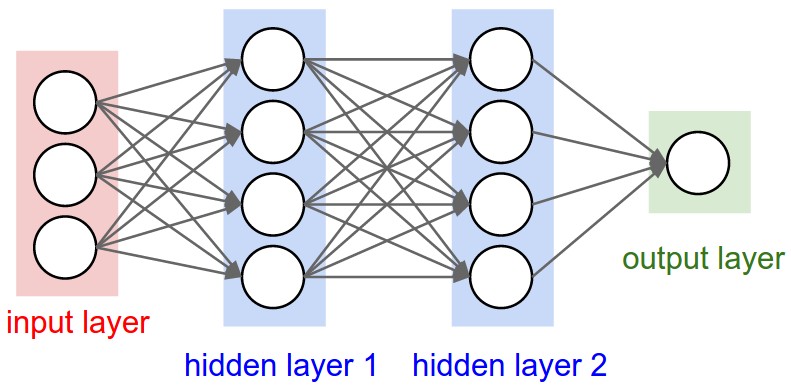
- QUOTE: ... Neural Network models are often organized into distinct layers of neurons. For regular neural networks, the most common layer type is the fully-connected layer in which neurons between two adjacent layers are fully pairwise connected, but neurons within a single layer share no connections. Below are two example Neural Network topologies that use a stack of fully-connected layers:
|
|
Left: A 2-layer Neural Network (one hidden layer of 4 neurons (or units) and one output layer with 2 neurons), and three inputs. Right:A 3-layer neural network with three inputs, two hidden layers of 4 neurons each and one output layer. Notice that in both cases there are connections (synapses) between neurons across layers, but not within a layer. |
- Naming conventions. Notice that when we say N-layer neural network, we do not count the input layer. Therefore, a single-layer neural network describes a network with no hidden layers (input directly mapped to output). In that sense, you can sometimes hear people say that logistic regression or SVMs are simply a special case of single-layer Neural Networks.
2017b
- (Santos, 2017) ⇒ https://leonardoaraujosantos.gitbooks.io/artificial-inteligence/content/neural_networks.html Retrieved: 2018-01-07
- QUOTE: Neural networks are examples of Non-Linear hypothesis, where the model can learn to classify much more complex relations. Also it scale better than Logistic Regression for large number of features.
It's formed by artificial neurons, where those neurons are organised in layers. We have 3 types of layers:
- QUOTE: Neural networks are examples of Non-Linear hypothesis, where the model can learn to classify much more complex relations. Also it scale better than Logistic Regression for large number of features.
- We classify the neural networks from their number of hidden layers and how they connect, for instance the network above have 2 hidden layers. Also if the neural network has/or not loops we can classify them as Recurrent or Feed-forward neural networks.
Neural networks from more than 2 hidden layers can be considered a deep neural network.
- We classify the neural networks from their number of hidden layers and how they connect, for instance the network above have 2 hidden layers. Also if the neural network has/or not loops we can classify them as Recurrent or Feed-forward neural networks.
2017c
- (Miikkulainen, 2017) ⇒ Risto Miikkulainen (2017) "Topology of a Neural Network". In: Sammut & Webb. (2017).
- QUOTE: The most common topology in supervised learning is the fully connected, three-layer, feedforward network (see Backpropagation and Radial Basis Function Networks): All input values to the network are connected to all neurons in the hidden layer (hidden because they are not visible in the input or output), the outputs of the hidden neurons are connected to all neurons in the output layer, and the activations of the output neurons constitute the output of the whole network. Such networks are popular partly because they are known theoretically to be universal function approximators (with, e.g., a sigmoid or Gaussian nonlinearity in the hidden layer neurons), although networks with more layers may be easier to train in practice (e.g., Cascade-Correlation). In particular, deep learning architectures (see Deep Learning) utilize multiple hidden layers to form a hierarchy of gradually more structured representations that support a supervised task on top.
2016
- (Zhao, 2016) ⇒ Peng Zhao, (2016). "R for Deep Learning (I): Build Fully Connected Neural Network from Scratch"
- QUOTE: Hidden layers are very various and it’s the core component in DNN. But in general, more hidden layers are needed to capture desired patterns in case the problem is more complex (non-linear).
2003
- (Aryal & Wang, 2003) ⇒ Aryal, D. R., & Wang, Y. W. (2003). Neural network Forecasting of the production level of Chinese construction industry. Journal of comparative international management, 6(2).
- QUOTE: Networks layers : The most common type of artificial neural network consists of three groups, or layers, of units: a layer of “input” units is connected to a layer of “hidden” units, which is connected to a layer of “output” units. The activity of the input units represents the raw information that is fed into the network. The activity of each hidden unit is determined by the activities of the input units and the weights on the connections between the input and the hidden units. The behavior of the output units depends on the activity of the hidden units and the weights between the hidden and output units.