Locally Weighted Regression for Control
A Locally Weighted Regression (LWR) for Control is a Control Task that is based on a Locally Weighted Learning Task.
- AKA: Kernel Shaping, Lazy Learning, Locally Weighted Learning, Local Distance Metric Adaptation, Nonstationary Kernels, Supersmoothing.
- Context:
- It can be solved by Locality Sensitive Hashing Based Clustering System that implements a Locality Sensitive Hashing Based Clustering Algorithm.
- Example(s):
- …
- Counter-Example(s):
- See: Learning Control, Locally Weighted Regression Algorithm, Locally Weighted Regression Algorithm, Locality-Sensitive Hashing (LSH) Algorithm.
References
2017a
- (Ting et al., 2017) ⇒ Jo-Anne Ting, Franzisk Meier, Sethu Vijayakumar, and Stefan Schaal (2017) "Locally Weighted Regression for Control". In: Sammut & Webb. (2017).
- QUOTE: Learning control refers to the process of acquiring a control strategy for a particular control system and a particular task by trial and error. It is usually distinguished from adaptive control (Aström and Wittenmark 1989) in that the learning system is permitted to fail during the process of learning, resembling how humans and animals acquire new movement strategies. In contrast, adaptive control emphasizes single-trial convergence without failure, fulfilling stringent performance constraints, e.g., as needed in life-critical systems like airplanes and industrial robots.
Locally weighted regression refers to supervised learning of continuous functions (otherwise known as function approximation or regression) by means of of spatially localized algorithms, which are often discussed in the context of kernel regression, nearest neighbor methods, or lazy learning (Atkeson et al. 1997) (...)
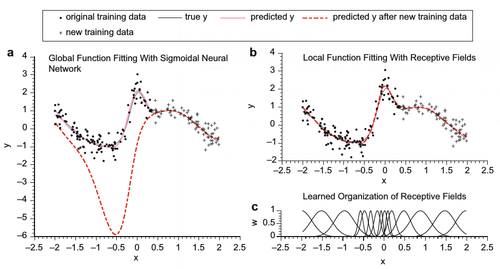
Figure 1 illustrates why locally weighted regression methods are often favored over global methods when it comes to learning from incrementally arriving data, especially when dealing with nonstationary input distributions. The figure shows the division of the training data into two sets: the “original training data” and the “new training data” (in dots and crosses, respectively).
Locally Weighted Regression for Control, Fig. 1. Function approximation results for the function [math]\displaystyle{ y= sin(2x) + 2 \exp( -16^2x) + N(0, 0.16) }[/math]with (a) a sigmoidal neural network, (b) a locally weighted regression algorithm (note that the data traces “true y,” “predicted y,” and “predicted y after new training data” largely coincide), and (c) the organization of the (Gaussian) kernels of (b) after training. See Schaal and Atkeson 1998 for more details.
- QUOTE: Learning control refers to the process of acquiring a control strategy for a particular control system and a particular task by trial and error. It is usually distinguished from adaptive control (Aström and Wittenmark 1989) in that the learning system is permitted to fail during the process of learning, resembling how humans and animals acquire new movement strategies. In contrast, adaptive control emphasizes single-trial convergence without failure, fulfilling stringent performance constraints, e.g., as needed in life-critical systems like airplanes and industrial robots.
2017b
- (Sammut & Webb, 2017) ⇒ (2017) "Learning Control". In: Sammut & Webb. (2017).
- QUOTE: Learning control refers to the process of acquiring a control strategy for a particular control system and a particular task by trial and error. Learning control is usually distinguished from adaptive control in that the learning system is permitted to fail during the process of learning. In contrast, adaptive control emphasizes single trial convergence without failure. Thus, learning control resembles the way that humans and animals acquire new movement strategies, while adaptive control is a special case of learning control that fulfills stringent performance constraints, e.g., as needed in life-critical systems like airplanes and industrial robots. In general, the control system can be any system that changes its state in response to a control signal, e.g., a web page with a hyperlink, a car, or a robot.
1997a
- (Atkeson et al., 1997a) ⇒ Christopher G. Atkeson, Andrew W. Moore, and Stefan Schaal. (1997). "Locally Weighted Learning for Control". In: Aha D.W. (eds) Lazy Learning. Springer, Dordrecht.
- ABSTRACT: Lazy learning methods provide useful representations and training algorithms for learning about complex phenomena during autonomous adaptive control of complex systems. This paper surveys ways in which locally weighted learning, a type of lazy learning, has been applied by us to control tasks. We explain various forms that control tasks can take, and how this affects the choice of learning paradigm. The discussion section explores the interesting impact that explicitly remembering all previous experiences has on the problem of learning to control.
1997b
- (Atkeson et al., 1997b) ⇒ Christopher G. Atkeson, Andrew W. Moore, and Stefan Schaal. (1997). "Locally weighted learning".
- QUOTE: In locally weighted regression (LWR) local models are fit to nearby data. As described later in this section, this can be derived by either weighting the training criterion for the local model (in the general case) or by directly weighting the data (in the case that the local model is linear in the unknown parameters). LWR is derived from standard regression procedures for global models.
1989
- (Astrom & Wittenmark, 1989) ⇒ K.J. Astrom, and B. Wittenmark (1989). Adaptive control. Addison-Wesley, Reading----