2019 AutoKerasAnEfficientNeuralArchi

• (Jin et al., 2019) ⇒ Haifeng Jin, Qingquan Song, and Xia Hu. (2019). “Auto-Keras: An Efficient Neural Architecture Search System.” In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ISBN:978-1-4503-6201-6 doi:10.1145/3292500.3330648. arXiv:1806.10282

Subject Headings: Auto-Keras System, Neural Architecture Search (NAS) System, Deep Neural Network, Automated Machine Learning (AutoML) System, Edit-Distance Neural Network Kernel, Bayesian Optimization Algorithm.

Notes

• Article Version: Eprint - arxiv:1806.10282, Open Access.

Cited By

• Google Scholar: ~ 7 Citations (Retrieved: 2019-10-20).
• ACM DL: ~ No Citations (Retrieved:2019-10-20).
• Semantic Scholar: ~ 5 Citations (Retrieved: 2019-10-20).

Quotes

Author Keywords

• Automated Machine Learning, AutoML, Neural Architecture Search, Bayesian Optimization, Network Morphism.

Abstract

Neural architecture search (NAS) has been proposed to automatically tune deep neural networks, but existing search algorithms, e.g., NASNet, PNAS, usually suffer from expensive computational cost. Network morphism, which keeps the functionality of a neural network while changing its neural architecture, could be helpful for NAS by enabling more efficient training during the search. In this paper, we propose a novel framework enabling Bayesian optimization to guide the network morphism for efficient neural architecture search. The framework develops a neural network kernel and a tree-structured acquisition function optimization algorithm to efficiently explores the search space. Extensive experiments on real-world benchmark datasets have been done to demonstrate the superior performance of the developed framework over the state-of-the-art methods. Moreover, we build an open-source AutoML system based on our method, namely Auto-Keras. The code and documentation are available at https://autokeras.com.

The system runs in parallel on CPU and GPU, with an adaptive search strategy for different GPU memory limits.

The code and documentation are available at https://autokeras.com

1 Introduction

Automated Machine Learning (AutoML) has become a very important research topic with wide applications of machine learning techniques. The goal of AutoML is to enable people with limited machine learning background knowledge to use the machine learning models easily. Work has been done on automated model selection, automated hyperparameter tunning, and etc. In the context of deep learning, neural architecture search (NAS), which aims to search for the best neural network architecture for the given learning task and dataset, has become an effective computational tool in AutoML. Unfortunately, existing NAS algorithms are usually computationally expensive. The time complexity of NAS is [math]\displaystyle{ O (nt) }[/math], where n is the number of neural architectures evaluated during the search, and [math]\displaystyle{ t }[/math] is the average time consumption for evaluating each of the [math]\displaystyle{ n }[/math] neural networks. Many NAS approaches, such as deep reinforcement learning [2, 30, 40, 41], gradient-based methods [26] and evolutionary algorithms [10, 23, 31, 32, 34], require a large [math]\displaystyle{ n }[/math] to reach a good performance. Also, each of the [math]\displaystyle{ n }[/math] neural networks is trained from scratch which is very slow.

Initial efforts have been devoted to making use of network morphism in neural architecture search [6, 11]. It is a technique to morph the architecture of a neural network but keep its functionality [8, 36]. Therefore, we are able to modify a trained neural network into a new architecture using the network morphism operations, e.g., inserting a layer or adding a skip-connection. Only a few more epochs are required to further train the new architecture towards better performance. Using network morphism would reduce the average training time 2? in neural architecture search. The most important problem to solve for network morphism-based NAS methods is the selection of operations, which is to select an operation from the network morphism operation set to morph an existing architecture to a new one. The network morphism-based NAS methods are not efficient enough. They either require a large number of training examples [6], or inefficient in exploring the large search space [11]. How to perform efficient neural architecture search with network morphism remains a challenging problem.

As we know, Bayesian optimization [33] has been widely adopted to efficiently explore black-box functions for global optimization, whose observations are expensive to obtain. For example, it has been used in hyperparameter tuning for machine learning models [13, 15, 17, 35], in which Bayesian optimization searches among different combinations of hyperparameters. During the search, each evaluation of a combination of hyperparameters involves an expensive process of training and testing the machine learning model, which is very similar to the NAS problem. The unique properties of Bayesian optimization motivate us to explore its capability in guiding the network morphism to reduce the number of trained neural networks n to make the search more efficient.

It is non-trivial to design a Bayesian optimization method for network morphism-based NAS due to the following challenges. First, the underlying Gaussian process (GP) is traditionally used for learning probability distribution of functions in Euclidean space. To update the Bayesian optimization model with observations, the underlying GP is to be trained with the searched architectures and their performances. However, the neural network architectures are not in Euclidean space and hard to parameterize into a fixed-length vector. Second, an acquisition function needs to be optimized for Bayesian optimization to generate the next architecture to observe. However, in the context of network morphism, it is not to maximize a function in Euclidean space, but finding a node in a tree-structured search space, where each node represents a neural architecture and each edge is a morph operation. Thus traditional gradient-based methods cannot be simply applied. Third, the changes caused by a network morphism operation is complicated. A network morphism operation on one layer may change the shapes of some intermediate output tensors, which no longer match input shape requirements of the layers taking them as input. How to maintain such consistency is a challenging problem.

In this paper, an efficient neural architecture search with network morphism is proposed, which utilizes Bayesian optimization to guide through the search space by selecting the most promising operations each time. To tackle the aforementioned challenges, an edit-distance neural network kernel is constructed. Being consistent with the key idea of network morphism, it measures how many operations are needed to change one neural network to another.

Besides, a novel acquisition function optimizer, which is capable of balancing between the exploration and exploitation, is designed specially for the tree-structure search space to enable Bayesian optimization to select from the operations. In addition, a graph-Ievel network morphism is defined to address the changes in the neural architectures based on layer-Ievel network morphism. The proposed approach is compared with the state-of-the-art NAS methods [11, 16] on benchmark datasets of MNIST, CIFARlO, and FASHION-MNIST. Within a limited search time, the architectures found by our method achieves the lowest error rates on all of the datasets.

In addition, we have developed a widely adopted open-source AutoML system based on our proposed method, namely Auto-Keras. It is an open—source AutoML system, which can be download and installed locally. The system is carefully designed with a concise interface for people not specialized in computer programming and data science to use. To speed up the search, the workload on CPU and CPU can run in parallel. To address the issue of different CPU memory, which limits the size of the neural architectures, a memory adaption strategy is designed for deployment.

The main contributions of the paper are as follows:

• Propose an algorithm for efficient neural architecture search based on network morphism guided by Bayesian optimization.
• Conduct intensive experiments on benchmark datasets to demonstrate the superior performance of the proposed method over the baseline methods.
• Develop an open-source system, namely Auto-Keras, which is one of the most widely used AutoML systems.

2 Problem Statement

The general neural architecture search problem we studied in this paper is defined as: Given a neural architecture search space T, the input data D divided into Dtmin and DWI, and the cost function Cost(-), we aim at finding an optimal neural network f * E T, which could achieve the lowest cost on dataset D. The definition is equivalent to finding f * satisfying:

(....)

where Cost(-, -) is the evaluation metric function, e.g., accuracy, mean squared error, 0* is the learned parameter of f .

The search space T covers all the neural architectures, which can be morphed from the initial architectures. The details of the morph operations are introduced in 3.3. Notably, the operations can change the number of filters in a convolutional layer, which makes T larger than methods with fixed layer width [24].

3 Network Morphism Guided By Bayesian Optimization

The key idea of the proposed method is to explore the search space Via morphing the neural architectures guided by Bayesian optimization (BO) algorithm. Traditional Bayesian optimization consists of a loop of three steps: update, generation, and observation. In the context of NAS, our proposed Bayesian optimization algorithm iteratively conducts: (1) Update: train the underlying Gaussian process model with the existing architectures and their performance; (2) Generation: generate the next architecture to observe by optimizing a delicately defined acquisition function; (3) Observation: obtain the actual performance by training the generated neural architecture. There are three main challenges in designing a method for morphing the neural architectures with Bayesian optimization. We introduce three key components separately in the subsequent sections coping with the three challenges.

3.1 Edit-Distance Neural Network Kernel for Gaussian Process

The first challenge we need to address is that the NAS space is not a Euclidean space, which does not satisfy the assumption of traditional Gaussian process (GP). Directly vectorizing the neural architecture is impractical due to the uncertain number of layers and parameters it may contain. Since the Gaussian process is a kernel method, instead of vectorizing a neural architecture, we propose to tackle the challenge by designing a neural network kernel function. The intuition behind the kernel function is the edit- distance for morphing one neural architecture to another. More edits needed from one architecture to another means the further distance between them, thus less similar they are. The proof of validity of the kernel function is presented in Appendix E.

Kernel Definition: Suppose fa and f}, are two neural networks. Inspired by Deep Graph Kernels [38], we propose an edit-distance kernel for neural networks. Edit-distance here means how many operations are needed to morph one neural network to another. The concrete kernel function is defined as:

(....)

where function d(-, -) denotes the edit-distance of two neural networks, whose range is [0, +00), p is a mapping function, which maps the distance in the original metric space to the corresponding distance in the new space. The new space is constructed by embedding the original metric space into a new one using Bourgain Theorem [3], which ensures the validity of the kernel.

Calculating the edit-distance of two neural networks can be mapped to calculating the edit-distance of two graphs, which is an NP-hard problem [39]. Based on the search space T defined in Section 2, we tackle the problem by proposing an approximated solution as follows:

(...)

where D; denotes the edit-distance for morphing the layers, i.e., the minimum edits needed to morph fa to f}, if the skip-connections are ignored, La = {1511),122), . . .} and L}, = {1(1), 122), . . .} are the layer sets of neural networks fa and fb, Ds is the approximated edit-distance for morphing skip-connections between two neural networks, SE = {3511), 3512), . . .} and S}, = {321), 322), . . .} are the skip- connection sets of neural network fa and fb, and x1 is the balancing factor between the distance of the layers and the skip-connections.

Calculating D]: We assume |Lu| < |Lbl, the edit-distance for morphing the layers of two neural architectures fa and fl, is calculated by minimizing the follow equation:

(....)

where 4); : Lu —> L}, is an injective matching function of layers satisfying: Vi < j, (0103)) < (0102”) if layers in La and L}, are all sorted in topological order. d l(-, -) denotes the edit-distance of widening a layer into another defined in Equation (6),

(...)

where w(l) is the width of layer 1.

The intuition of Equation (5) is consistent with the idea of network morphism shown in Figure 1. Suppose a matching is provided between the nodes in two neural networks. The sizes of the tensors are indicators of the width of the previous layers (e.g., the output vector length of a fully-connected layer or the number of filters of a convolutional layer). The matchings between the nodes are marked by light blue. So a matching between the nodes can be seen as matching between the layers. To morph fa to f}, with the given matching, we need to first widen the three nodes in fa to the same width as their matched nodes in fb, and then insert a new node of width 20 after the first node in fa. Based on this morphing scheme, the edit-distance of the layers is defined as D; in Equation (5).

Since there are many ways to morph fa to fb, to find the best matching between the nodes that minimizes D], we propose a dynamic programming approach by defining a matrix A] La l><l Lb ‘, which is recursively calculated as follows:

(...)

Calculating D3: The intuition of D3 is the sum of the edit-distances of the matched skip-connections in two neural networks into pairs. As shown in Figure 1, the skip-connections with the same color are matched pairs. Similar to Dl(-, -), Ds(-, -) is defined as follows:

(...)

where we assume |Sa| < |Sbl. (|Sbl — |Sul) measures the total edit- distance for non-matched skip-connections since each of the non- matched skip-connections in 5;, calls for an edit of inserting a new skip connection into fa. The mapping function ([13 : Su —> S}, is an injective function. d s(-, -) is the edit-distance for two matched skip-connections defined as:

(...)

where u(s) is the topological rank of the layer the skip-connection s started from, 5(3) is the number of layers between the start and end point of the skip-connection s. This minimization problem in Equation (8) can be mapped to a bipartite graph matching problem, where fa and f}, are the two disjoint sets of the graph, each skip-connection is a node in its corresponding set. The edit-distance between two skip-connections is the weight of the edge between them. The weighted bipartite graph matching problem is solved by the Hungarian algorithm (Kuhn-Munkres algorithm) [19].

Figure 1: Neural Network Kernel. Given two neural networks [math]\displaystyle{ f_a }[/math], [math]\displaystyle{ f_b }[/math], and matchings between the similar layers, the figure shows how the layers of [math]\displaystyle{ f_a }[/math] can be changed to the same as [math]\displaystyle{ f_b }[/math]. Similarly, the skip-connections in [math]\displaystyle{ f_a }[/math] also need to be changed to the same as [math]\displaystyle{ f_b }[/math], according to a given matching.

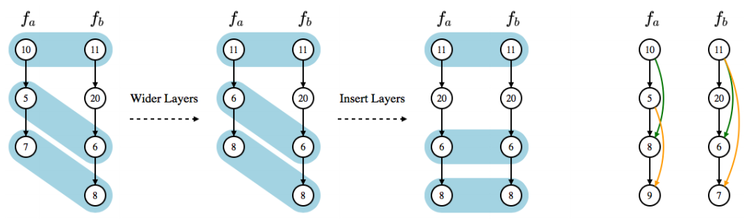
==== 3.2 Optimization for Tree Structured Space ==== The second challenge of using Bayesian optimization to guide network morphism is the optimization of the acquisition function. The traditional acquisition functions are defined on Euclidean space. The optimization methods are not applicable to the tree-structured search Via network morphism. To optimize our acquisition function, we need a method to efficiently optimize the acquisition function in the tree-structured space. To deal with this problem, we propose a novel method to optimize the acquisition function on tree-structured space.

 Upper-confidence bound (UCB) [1 is selected as our acquisition function, which is defined as:

[math]\displaystyle{ \alpha(f) = \mu(y_f) - \beta\sigma(y_f), \quad\quad (10) }[/math]

where [math]\displaystyle{ y_f = Cost(f, D) }[/math], [math]\displaystyle{ \beta }[/math] is the balancing factor, [math]\displaystyle{ \mu(y_f) }[/math] and [math]\displaystyle{ \sigma(y_f) }[/math] are the posterior mean and standard deviation of variable [math]\displaystyle{ y_f }[/math]. It has two important properties, which fit our problem. First, it has an explicit balance factor [math]\displaystyle{ \beta }[/math] for exploration and exploitation. Second, [math]\displaystyle{ \alpha(f) }[/math] is directly comparable with the cost function value [math]\displaystyle{ c^{(i)} }[/math] in search history [math]\displaystyle{ \mathcal{H} = \{(f^{(i)},\theta^{(i)}, c^{(i)}\} }[/math]. It estimates the lowest possible cost given the neural network [math]\displaystyle{ f\cdot\hat{f} = argmin_f\alpha(f) }[/math] is the generated neural architecture for next observation.

The tree-structured space is defined as follows. During the optimization of [math]\displaystyle{ \alpha(f) }[/math], [math]\displaystyle{ \hat{f} }[/math] should be obtained from [math]\displaystyle{ f^{(i)} }[/math] and [math]\displaystyle{ \mathcal{O} }[/math], where [math]\displaystyle{ f^{(i)} }[/math] is an observed architecture in the search history [math]\displaystyle{ \mathcal{H} }[/math], [math]\displaystyle{ \mathcal{O} }[/math] is a sequence of operations to morph the architecture into a new one. Morph [math]\displaystyle{ f }[/math] to [math]\displaystyle{ \hat{f} }[/math] with [math]\displaystyle{ \mathcal{O} }[/math] is denoted as [math]\displaystyle{ \hat{f} \leftarrow \mathcal{M}(f,\mathcal{O}) }[/math], where [math]\displaystyle{ \mathcal{M}(\cdot, \cdot) }[/math] is the function to morph [math]\displaystyle{ f }[/math] with the operations in [math]\displaystyle{ \mathcal{O} }[/math]. Therefore, the search can be viewed as a tree-structured search, where each node is a neural architecture, whose children are morphed from it by network morphism operations.

The most common defect of network morphism is it only grows the size of the architecture instead of shrinking them. Using network morphism for NAS may end up with a very large architecture without enough exploration on the smaller architectures. However, our tree-structure search, we not only expand the leaves but also the inner nodes, which means the smaller architectures found in the early stage can be selected multiple times to morph to more comparatively small architectures.

Inspired by various heuristic search algorithms for exploring the tree-structured search space and optimization methods balancing between exploration and exploitation, a new method based on a search and simulated annealing is proposed. [math]\displaystyle{ A^{\star} }[/math] algorithm is widely used for tree-structure search. It maintains a priority queue of nodes and keeps expanding the best node in the queue. Since [math]\displaystyle{ A^{\star} }[/math] always exploits the best node, simulated annealing is introduced to balance the exploration and exploitation by not selecting the estimated best architecture with a probability.

As shown in Algorithm 1, the algorithm takes minimum temperature [math]\displaystyle{ T_{low} }[/math], temperature decreasing rate [math]\displaystyle{ r }[/math] for simulated annealing, and search history [math]\displaystyle{ \mathcal{H} }[/math] described in Section 2 as the input. It outputs a neural architecture [math]\displaystyle{ f \in \mathcal{H} }[/math] and a sequence of operations [math]\displaystyle{ \mathcal{O} }[/math] to morph [math]\displaystyle{ f }[/math] into the new architecture. From line 2 to 6, the searched architectures are pushed into the priority queue, which sorts the elements according to the cost function value or the acquisition function value. Since UCB is chosen as the acquisition function, [math]\displaystyle{ \alpha(f) }[/math] is directly comparable with the history observation values [math]\displaystyle{ c^{(i)} }[/math]. From line 7 to 18, it is the loop optimizing the acquisition function. Following the setting in [math]\displaystyle{ A^{\star} }[/math] search, in each iteration, the architecture with the lowest acquisition function value is popped out to be expanded on line 8 to 10, where [math]\displaystyle{ \Omega(f) }[/math] is all the possible operations to morph the architecture [math]\displaystyle{ f, \mathcal{M}( f , o) }[/math] is the function to morph the architecture [math]\displaystyle{ f }[/math] with the operation sequence [math]\displaystyle{ o }[/math]. However, not all the children are pushed into the priority queue for exploration purpose. The decision of whether it is pushed into the queue is made by simulated annealing on line 11, where

[math]\displaystyle{ \exp\left(\dfrac{c_{min} \alpha(f')}{T}\right) }[/math]

is a typical acceptance function in simulated annealing. [math]\displaystyle{ c_{min} }[/math] and [math]\displaystyle{ f_{min} }[/math] are updated from line 14 to 16, which record the minimum acquisition function value and the corresponding architecture.

3.3 Graph-Level Network Morphism

The third challenge is to maintain the intermediate output tensor shape consistency when morphing the architectures. Previous work showed how to preserve the functionality of the layers the operators applied on, namely layer-level morphism. However, from a graph- level View, any change of a single layer could have a butterfly effect on the entire network. Otherwise, it would break the input and output tensor shape consistency. To tackle the challenge, a graph- level morphism is proposed to find and morph the layers influenced by a layer-level operation in the entire network.

Follow the four network morphism operations on a neural net- work f E T defined in [11], which can all be reflected in the change of the computational graph G. The first operation is inserting a layer to f to make it deeper denoted as deep(G,u), where u is the node marking the place to insert the layer. The second one is widening a node in f denoted as wide(G, u), where u is the node representing the intermediate output tensor to be widened. Widen here could be either making the output vector of the previous fully- connected layer of u longer, or adding more filters to the previous convolutional layer of u, depending on the type of the previous layer. The third is adding an additive connection from node u to node v denoted as add(G, u, v). The fourth is adding an concatena- tive connection from node u to node v denoted as concat(G, u, v). For d eep(G, u), no other operation is needed except for initializing the weights of the newly added layer. However, for all other three operations, more changes are required to G.

First, we define an effective area of wide(G, no) as y to better describe where to change in the network. The effective area is a set of nodes in the computational graph, which can be recursively defined by the following rules: 1. no 6 y. 2.1) E y, if 3'8qu ¢ Ls, u E y. 3. v E y, ifElevHu ¢ Ls, u E y. L3 is the set offully-connected layers and convolutional layers. Operation wide(G, uo) needs to change two set of layers, the previous layer set LP = {(3qu E lev E y}, which needs to output a wider tensor, and next layer set L" = {(3qu 6 L3 lu E y}, which needs to input a wider tensor. Second, for operator add(G, no, Do), additional pooling layers may be needed on the skip-connection. no and Do have the same number of channels, but their shape may differ because of the pooling layers between them. So we need a set ofpooling layers whose effect is the same as the combination of all the pooling layers between no and Do, which is defined as L0 = {e E Lpaalle E puflfivfl}. where puflfiv0 could be any path between no and Do, Lpool is the pooling layer set. Another layer LC is used after to pooling layers to process no to the same width as Do. Third, in concat(G, no, Do), the concatenated tensor is wider than the original tensor Do. The concatenated tensor is input to a new layer LC to reduce the width back to the same width as Do. Additional pooling layers are also needed for the concatenative connection.

3.4 Time Complexity Analysis

As described at the start of Section 3, Bayesian optimization can be roughly divided into three steps: update, generation, and obser- vation. The bottleneck of the algorithm efficiency is observation, which involves the training of the generated neural architecture. Let n be the number of architectures in the search history. The time complexity of the update is O(n2 log2 n). In each generation, the ker- nel is computed between the new architectures during optimizing acquisition function and the ones in the search history, the number ofvalues in which is O(nm), where m is the number of architectures computed during the optimization of the acquisition function. The time complexity for computing d(-, -) once is O(l2 + 33), where l and s are the number of layers and skip-connections. So the overall time complexity is O(nm(l2 + 33) + n2 log2 n). The magnitude of these factors is within the scope of tens. So the time consumption of update and generation is trivial comparing to the observation.

4 Auto-Keras

Based on the proposed neural architecture search method, we developed an open-source AutoML system, namely Auto-Keras. It is named after Keras [9], which is known for its simplicity in creating neural networks. Similar to SMAC [15], TPOT [28], Auto- WEKA [35], and Auto-Sklearn [13], the goal is to enable domain experts who are not familiar with machine learning technologies to use machine learning techniques easily. However, Auto-Keras is focusing on the deep learning tasks, which is different from the systems focusing on the shallow models mentioned above.

Although, there are several AutoML services available on large cloud computing platforms, three things are prohibiting the users from using them. First, the cloud services are not free to use, which may not be affordable for everyone who wants to use AutoML techniques. Second, the cloud-based AutoML usually requires complicated configurations ofDocker containers and Kubernetes, which is not easy for people without a rich computer science background. Third, the AutoML service providers are honest-but-curious [7], which cannot guarantee the security and privacy of the data. An open-source software, which is easily downloadable and runs 10- cally, would solve these problems and make the AutoML accessible to everyone. To bridge the gap, we developed Auto-Keras.

It is challenging, to design an easy-to-use and locally deployable system. First, we need a concise and configurable application programming interface (API). For the users who don’t have rich experience in programming, they could easily learn how to use the API. For the advanced users, they can still configure the details of the system to meet their requirements. Second, the local computation resources may be limited. We need to make full use of the local computation resources to speed up the search. Third, the available GPU memory may be of different sizes in different environments. We need to adapt the neural architecture sizes to the GPU memory during the search.

4.1 System Overview

The system architecture of Auto-Keras is shown in Figure 2. We design this architecture to fully make use of the computational resource of both CPU and GPU, and utilize the memory efficiently by only placing the currently useful information on the RAM, and save the rest on the storage devices, e.g., hard drives. The top part is the API, which is directly called by the users. It is responsible for calling corresponding middle-level modules to complete certain functionalities. The Searcher is the module of the neural architecture search algorithm containing Bayesian Optimizer and Gaussian Process. These search algorithms run on CPU. The Model Trainer is a module responsible for the computation on GPUs. It trains given neural networks with the training data in a separate process for parallelism. The Graph is the module processing the computational graphs of neural networks, which is controlled by the Searcher for the network morphism operations. The current neural architecture in the Graph is placed on RAM for faster access. The Model Storage is a pool of trained models. Since the size of the neural networks are large and cannot be stored all in memory, the model storage saves all the trained models on the storage devices.

A typical workflow for the Auto-Keras system is as follows. The user initiated a search for the best neural architecture for the dataset. The API received the call, preprocess the dataset, and pass it to the Searcher to start the search. The Bayesian Optimizer in the Searcher would generate a new architecture using CPU. It calls the Graph module to build the generated neural architecture into a real neural network in the RAM. The new neural architecture is copied the GPU for the Model Trainer to train with the dataset. The trained model is saved in the Model Storage. The performance of the model is feedback to the Searcher to update the Gaussian Process.

Figure 2: Auto-Keras System Overview. (1) User calls the API. (2) The searcher generates neural architectures on CPU. (3) Graph builds real neural networks with parameters on RAM from the neural architectures. (4) The neural network is copied to GPU for training. (5) Trained neural networks are saved on storage devices.

==== 4.2 Application Programming Interface ====

The design of the API follows the classic design of the Scikit-Learn API [5, 29], which is concise and configurable. The training of a neural network requires as few as three lines of code calling the constructor, the fit and predict function respectively. To accommo- date the needs of different users, we designed two levels of APIs. The first level is named as task-level. The users only need to know their task, e.g., Image Classification, Text Regression, to use the API. The second level is named search-level, which is for advanced users. The user can search for a specific type of neural network architectures, e.g., multi-layer perceptron, convolutional neural network. To use this API, they need to preprocess the dataset by themselves and know which type of neural network, e.g., CNN or MLP, is the best for their task.

Several accommodations have been implemented to enhance the user experience with the Auto-Keras package. First, the user can restore and continue a previous search which might be accidentally killed. From the users’ perspective, the main difference of using Auto-Keras comparing with the AutoML systems aiming at shallow models is the much longer time consumption, since a number of deep neural networks are trained during the neural architecture search. It is possible for some accident to happen to kill the pro- cess before the search finishes. Therefore, the search outputs all the searched neural network architectures with their trained pa- rameters into a specific directory on the disk. As long as the path to the directory is provided, the previous search can be restored. Second, the user can export the search results, which are neural architectures, as saved Keras models for other usages. Third, for advanced users, they can specify all kinds of hyperparameters of the search process and neural network optimization process by the default parameters in the interface.

4.3 CPU and GPU Parallelism

To make full use of the limited local computation resources, the program can run in parallel on the GPU and the CPU at the same time. If we do the observation (training of the current neural network), update, and generation of Bayesian optimization in sequential order. The GPUs will be idle during the update and generation. The CPUs will be idle during the observation. To improve the efficiency, the observation is run in parallel with the generation in separated processes. A training queue is maintained as a buffer for the Model Trainer. Figure 3 shows the sequence diagram of the parallelism between the CPU and the GPU. First, the Searcher requests the queue to pop out a new graph and pass it to GPU to start training. Second, while the GPU is busy, the searcher requests the CPU to generate a new graph. At this time period, the GPU and the CPU work in parallel. Third, the CPU returns the generated graph to the searcher, who pushes the graph into the queue. Finally, the Model Trainer finished training the graph on the GPU and returns it to the Searcher to update the Gaussian process. In this way, the idle time of GPU and CPU are dramatically reduced to improve the efficiency of the search process.

Figure 3: CPU and GPU Parallelism. During training the current neural architecture on GPU, CPU generates the next neural architecture (graph).

==== 4.4 GPU Memory Adaption ====

Since different deployment environments have different limitations on the GPU memory usage, the size of the neural networks needs to be limited according to the GPU memory. Otherwise, the system would crash because of running out of GPU memory. To tackle this challenge, we implement a memory estimation function on our own data structure for the neural architectures. An integer value is used to mark the upper bound of the neural architecture size. Any new computational graph whose estimated size exceeds the upper bound is discarded. However, the system may still crash because the management of the GPU memory is very complicated, which cannot be precisely estimated. So whenever it runs out of GPU memory, the upper bound is lowered down to further limit the size of the generated neural networks.

5 Experiments

In the experiments, we aim at answering the following questions. 1) How effective is the search algorithm with limited running time? 2) How much efficiency is gained from Bayesian optimization and network morphism? 3) What are the influences of the important hyperparameters of the search algorithm? 4) Does the proposed kernel function correctly measure the similarity among neural networks in terms of their actual performance?

Datasets Three benchmark datasets, MNIST [20], CIFARIO [18], and FASHION [37] are used in the experiments to evaluate our method. They prefer very different neural architectures to achieve good performance.

Baselines Four categories of baseline methods are used for comparison, which are elaborated as follows:

• Straightforward Methods: random search (RAND) and grid search (GRJD). They search the number of convolutional layers and the width of those layers.
• Conventional Methods: SPMT [33] and SMAC [15]. Both SPMT and SMAC are designed for general hyperparameters tuning tasks of machine learning models instead of focusing on the deep neural networks. They tune the 16 hyperparameters of a three-layer convolutional neural network, including the width, dropout rate, and regularization rate of each layer.
• State-of-the-art Methods: SEAS [11], NASBOT [16]. We carefully implemented the SEAS as described in their paper. For NAS- BOT, since the experimental settings are very similar, we directly trained their searched neural architecture in the paper. They did not search architectures for MNIST and FASIHON dataset, so the results are omitted in our experiments.
• Variants of the proposed method: BFS and B0. Our proposed method is denoted as AK. BFS replaces the Bayesian optimization in AK with the breadth-first search. B0 is another variant, which does not employ network morphism to speed up the training. For AK, [math]\displaystyle{ \beta }[/math] is set to 2.5, while [math]\displaystyle{ \lambda }[/math] is set to 1 according to the parameter sensitivity analysis.

In addition, the performance of the deployed system of Auto-Keras (AK-DP) is also evaluated in the experiments. The difference from the AK above is that AK-DP uses various advanced techniques to improve the performance including learning rate scheduling, multiple manually defined initial architectures.

Experimental Setting The general experimental setting for evaluation is described as follows: First, the original training data of each dataset is further divided into training and validation sets by 80-20. Second, the testing data of each dataset is used as the testing set. Third, the initial architecture for SEAS, BO, BFS, and AK is a three-layer convolutional neural network with 64 filters in each layer. Fourth, each method is run for 12 hours on a single GPU (NVIDIA GeForce GTX 1080 Ti) on the training and validation set with batch size of 64. Fifth, the output architecture is trained with both the training and validation set. Sixth, the testing set is used to evaluate the trained architecture. Error rate is selected as the evaluation metric since all the datasets are for classification. For a fair comparison, the same data processing and training procedures are used for all the methods. The neural networks are trained for 200 epochs in all the experiments. Notably, AK-DP uses a real deployed system setting, whose result is not directly comparable with the rest of the methods. Except for AK-DP, all other methods are fairly compared using the same initial architecture to start the search.

5.1 Evaluation of Effectiveness

We first evaluate the effectiveness of the proposed method. The results are shown in Table 1. The following conclusions can be drawn based on the results.

(1) AK-DP is evaluated to show the final performance of our system, which shows deployed system (AK-DP) achieved state-of-the-art performance on all three datasets.

(2) The proposed method AK achieves the lowest error rate on all the three datasets, which demonstrates that AK is able to find simple but effective architectures on small datasets (MNIST) and can explore more complicated structures on larger datasets (CIFAR10).

(3) The straightforward approaches and traditional approaches perform well on the MNIST dataset, but poorly on the CIFARlO dataset. This may come from the fact that: naive approaches like random search and grid search only try a limited number of architectures blindly while the two conventional approaches are unable to change the depth and skip-connections of the architectures.

(4) Though the two state-of-the-art approaches achieve acceptable performance, SEAS could not beat our proposed model due to its subpar search strategy. The hill-climbing strategy it adopts only takes one step at each time in morphing the current best architecture, and the search tree structure is constrained to be unidirectionally extending. Comparatively speaking, NASBOT possesses stronger search expandability and also uses Bayesian optimization as our proposed method. However, the low efficiency in training the neural architectures constrains its power in achieving comparable performance within a short time period. By contrast, the network morphism scheme along with the novel searching strategy ensures our model to achieve desirable performance with limited hardware resources and time budges.

(5) For the two variants of AK, BFS preferentially considers searching a vast number of neighbors surrounding the initial architecture, which constrains its power in reaching the better architectures away from the initialization. By comparison, BO can jump far from the initial architecture. But without network morphism, it needs to train each neural architecture with much longer time, which limits the number of architectures it can search within a given time.

Table 1: Classification Error Rate.

Methods	MNIST	CIFAR10	FASHION
RANDOM	1.79%	16.86%	11.36%
GRID	1.68%	17.17%	10.28%
SPMT	1.36%	14.68%	9.62%
SMAC	1.43%	15.04%	10.87%
SEAS	1.07%	12.43%	8.05%
NASBOT	NA	12.30%	NA
BFS	1.56%	13.84%	9.13%
B0	1.83%	12.90%	7.99%
AK	0.55%	11.44%	7.42%
AK-DP	0.60%	3.60%	6.72%

5.2 Evaluation of Efficiency

In this experiment, we try to evaluate the efficiency gain of the proposed method in two aspects. First, we evaluate whether Bayesian optimization can really find better solutions with a limited number of observations. Second, we evaluated whether network morphism can enhance the training efl'iciency.

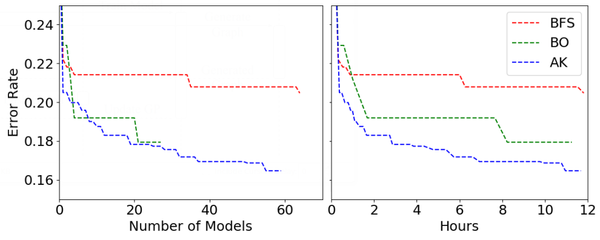
We compare the proposed method AK with its two variants, BFS and B0, to show the efficiency gains from Bayesian optimization and network morphism, respectively. BFS does not adopt Bayesian optimization but only network morphism, and use breadth-first search to select the network morphism operations. BO does not employ network morphism but only Bayesian optimization. Each of the three methods is run on CIFAR10 for twelve hours. The left part of Figure 4 shows the relation between the lowest error rate achieved and the number of neural networks searched. The right part of Figure 4 shows the relation between the lowest error rate achieved and the searching time.

Two conclusions can be drawn by comparing BFS and AK. First, Bayesian optimization can efficiently find better architectures with a limited number of observations. When searched the same number of neural architectures, AK could achieve a much lower error rate than BFS. It demonstrates that Bayesian optimization could effectively guide the search in the right direction, which is much more efficient in finding good architectures than the naive BFS approach. Second, the overhead created by Bayesian optimization during the search is low. In the left part of Figure 4, it shows BFS and AK searched similar numbers of neural networks within twelve hours. BFS is a naive search strategy, which does not consume much time during the search besides training the neural networks. AK searched slightly less neural architectures than BFS because of higher time complexity.

Two conclusions can be drawn by comparing B0 and AK. First, network morphism does not negatively impact the search performance. In the left part of Figure 4, when B0 and AK search a similar number of neural architectures, they achieve similar lowest error rates. Second, network morphism increases the training efficiency, thus improve the performance. As shown in left part of Figure 4, AK could search much more architectures than BO within the same amount of time due to the adoption of network morphism. Since network morphism does not degrade the search performance, searching more architectures results in finding better architectures. This could also be confirmed in the right part of Figure 4. At the end of the searching time, AK achieves lower error rate than B0.

Figure 4: Evaluation of Efficiency. The two figures plot the same result with different X-axis. BFS uses network morphism. BO uses Bayesian optimization. AK uses both.

==== 5.3 Parameter Sensitivity Analysis ====

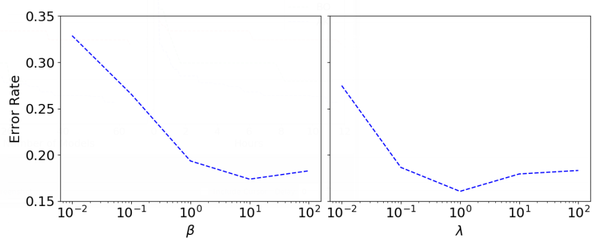
We now analyze the impacts of the two most important hyperparameters in our proposed method, i.e., [math]\displaystyle{ \beta }[/math] in Equation (10) balancing the exploration and exploitation of the search strategy, and [math]\displaystyle{ \lambda }[/math] in Equation (4) balancing the distance of layers and skip connections. For other hyperparameters, since [math]\displaystyle{ r }[/math] and [math]\displaystyle{ T_low }[/math] in Algorithm 1 are just normal hyperparameters of simulated annealing instead of important parameters directly related to neural architecture search, we do not delve into them here. In this experiment, we use the CIFAR10 dataset as an example. The rest of the experimental setting follows the setting of Section 5.1.

From Figure 5, we can observe that the influences of [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \lambda }[/math] to the performance of our method are similar. As shown in the left part of Figure 5, with the increase of[math]\displaystyle{ \beta }[/math] from 10’2 to 102, the error rate decreases first and then increases. If [math]\displaystyle{ \beta }[/math] is too small, the search process is not explorative enough to search the architectures far from the initial architecture. If it is too large, the search process would keep exploring the far points instead of trying the most promising architectures. Similarly, as shown in the right part of Figure 5, the increase of [math]\displaystyle{ \lambda }[/math] would downgrade the error rate at first and then upgrade it. This is because if [math]\displaystyle{ \lambda }[/math] is too small, the differences in the skip-connections of two neural architectures are ignored; conversely, if it is too large, the differences in the convolutional or fully-connected layers are ignored. The differences in layers and skip-connections should be balanced in the kernel function for the entire framework to achieve a good performance.

Figure 5: Parameter Sensitivity Analysis. [math]\displaystyle{ \beta }[/math] balances the exploration and exploitation of the search strategy. [math]\displaystyle{ \lambda }[/math] balances the distance of layers and skip connections.

==== 5.4 Evaluation of Kernel Quality ====

To show the quality of the edit-distance neural network kernel, we investigate the difference between the two matrices K and P. K "X" is the kernel matrix, where Ki’j = K(f(i),f0)). Pan describes the similarity of the actual performance between neural networks, where PM = —|c(i) —c(7)|, C”) is the cost function value in the search history 'H described in Section 3. We use CIFAR10 as an example here, and adopt error rate as the cost metric. Since the values in K and P are in different scales, both matrices are normalized to the range [—1, 1]. We quantitatively measure the difference between K and P with mean square error, which is 1.12 X 1071.

K and P are Visualized in Figure 6a and 6b. Lighter color means larger values. There are two patterns can be observed in the figures.

First, the white diagonal of Figure 6a and 6b. According to the definiteness property of the kernel, K(fx, fx) = 1, fo E T, thus the diagonal of K is always 1. It is the same for P since no difference exists in the performance of the same neural network.

Second, there is a small light square area on the upper left of Figure 6a. These are the initial neural architectures to train the Bayesian optimizer, which are neighbors to each other in terms of network morphism operations. A similar pattern is reflected in Figure 6b, which indicates that when the kernel measures two architectures as similar, they tend to have similar performance

Figure 6: Kernel and Performance Matrix Visualization. (a) shows the proposed kernel matrix. (b) is a matrix of similarity in the performance of the neural architectures.

=== 6 Conclusion And Future Work ===

In this paper, a novel method for efficient neural architecture search with network morphism is proposed. It enables Bayesian optimization to guide the search by designing a neural network kernel, and an algorithm for optimizing acquisition function in tree-structured space. The proposed method is wrapped into an open-source AutoML system, namely Auto-Keras, which can be easily downloaded and used with an extremely simple interface. The method has shown good performance in the experiments and outperformed several traditional hyperparameter-tuning methods and state-of-the-art neural architecture search methods. We plan to study the following open questions in future work. (1) The search space may be expanded to the recurrent neural networks. (2) Tune the neural architecture and the hyperparameters of the training process jointly. (3) Design task-oriented NAS to solve specific machine learning problems, e.g., image segmentation [21] and object detection [25].

References

• 1. Peter Auer, Nicolo Cesa-Bianchi, and Paul Fischer. 2002. Finite-time Analysis of the Multiarmed Bandit Problem. Machine Learning (2002).
• 2. Bowen Baker, Otkrist Gupta, Nikhil Naik, and Ramesh Raskar. 2016. Designing Neural Network Architectures Using Reinforcement Learning. ArXiv Preprint ArXiv:1611.02167 (2016).
• 3. James Bergstra, Dan Yamins, and David D Cox. 2013. Hyperopt: A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms. In Python in Science Conference .
• 4. Jean Bourgain. 1985. On Lipschitz Embedding of Finite Metric Spaces in Hilbert Space. Israel Journal of Mathematics (1985).
• 5. Andrew Brock, Theodore Lim, James M Ritchie, and Nick Weston. 2017. SMASH: One-shot Model Architecture Search through Hypernetworks. ArXiv Preprint ArXiv:1708.05344 (2017).
• 6. Lars Buitinck, Gilles Louppe, Mathieu Blondel, Fabian Pedregosa, Andreas Mueller, Olivier Grisel, Vlad Niculae, Peter Prettenhofer, Alexandre Gramfort, Jaques Grobler, Et Almbox. 2013. API Design for Machine Learning Software: Experiences from the Scikit-learn Project. In ECML PKDD Workshop: Languages for Data Mining and Machine Learning .
• 7. Han Cai, Tianyao Chen, Weinan Zhang, Yong Yu, and Jun Wang. 2018. Efficient Architecture Search by Network Transformation. In AAAI Conference on Artificial Intelligence .
• 8. Han Cai, Ligeng Zhu, and Song Han. 2019. ProxylessNAS: Direct Neural Architecture Search on Target Task and Hardware. In: Proceedings of The International Conference on Learning Representations .
• 9. Qi Chai and Guang Gong. 2012. Verifiable Symmetric Searchable Encryption for Semi-honest-but-curious Cloud Servers. In: Proceedings of The International Conference on Communications .
• 10. Tianqi Chen, Ian Goodfellow, and Jonathon Shlens. 2015. Net2net: Accelerating Learning via Knowledge Transfer. ArXiv Preprint ArXiv:1511.05641 (2015).
• 11. Franccois Chollet Et Almbox. 2015. Keras. Https://keras.io .
• 12. Travis Desell. 2017. Large Scale Evolution of Convolutional Neural Networks Using Volunteer Computing. In Genetic and Evolutionary Computation Conference Companion .
• 13. Thomas Elsken, Jan-Hendrik Metzen, and Frank Hutter. 2017. Simple And Efficient Architecture Search for Convolutional Neural Networks. ArXiv Preprint ArXiv:1711.04528 (2017).
• 14. Thomas Elsken, Jan Hendrik Metzen, and Frank Hutter. 2018. Neural Architecture Search: A Survey. ArXiv Preprint ArXiv:1808.05377 (2018).
• 15. Matthias Feurer, Aaron Klein, Katharina Eggensperger, Jost Springenberg, Manuel Blum, and Frank Hutter. 2015. Efficient and Robust Automated Machine Learning. In Advances in Neural Information Processing Systems .
• 16. Golnaz Ghiasi, Tsung-Yi Lin, Ruoming Pang, and Quoc V Le. 2019. NAS-FPN: Learning Scalable Feature Pyramid Architecture for Object Detection. ArXiv Preprint ArXiv:1904.07392 (2019).
• 17. Zichao Guo, Xiangyu Zhang, Haoyuan Mu, Wen Heng, Zechun Liu, Yichen Wei, and Jian Sun. 2019. Single Path One-Shot Neural Architecture Search with Uniform Sampling. ArXiv Preprint ArXiv:1904.00420 (2019).
• 18. Bernard Haasdonk and Claus Bahlmann. 2004. Learning with Distance Substitution Kernels. In Joint Pattern Recognition Symposium .
• 19. Peter E Hart, Nils J Nilsson, and Bertram Raphael. 1968. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Transactions on Systems Science and Cybernetics (1968).
• 20. Xiao Huang, Qiangquan Song, Fan Yang, and Xia Hu. 2019. Large-scale Heterogeneous Feature Embedding. In AAAI Conference on Artificial Intelligence .
• 21. Frank Hutter, Holger H Hoos, and Kevin Leyton-Brown. 2011. Sequential Model-Based Optimization for General Algorithm Configuration. In: Proceedings of The International Conference on Learning and Intelligent Optimization .
• 22. Kirthevasan Kandasamy, Willie Neiswanger, Jeff Schneider, Barnabas Poczos, and Eric Xing. 2018. Neural Architecture Search with Bayesian Optimisation and Optimal Transport. Advances in Neural Information Processing Systems (2018).
• 23. Scott Kirkpatrick, C Daniel Gelatt, and Mario P Vecchi. 1983. Optimization by Simulated Annealing. Science (1983).
• 24. Lars Kotthoff, Chris Thornton, Holger H Hoos, Frank Hutter, and Kevin Leyton-Brown. 2016. Auto-WEKA 2.0: Automatic Model Selection and Hyperparameter Optimization in WEKA. Journal of Machine Learning Research (2016).
• 25. Alex Krizhevsky and Geoffrey Hinton. 2009. Learning Multiple Layers of Features from Tiny Images . Technical Report. Citeseer.
• 26. Harold W Kuhn. 1955. The Hungarian Method for the Assignment Problem. Naval Research Logistics (1955).
• 27. Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. 1998. Gradient-based Learning Applied to Document Recognition. Proc. IEEE (1998).
• 28. Chenxi Liu, Liang-Chieh Chen, Florian Schroff, Hartwig Adam, Wei Hua, Alan Yuille, and Li Fei-Fei. 2019. Auto-DeepLab: Hierarchical Neural Architecture Search for Semantic Image Segmentation. ArXiv Preprint ArXiv:1901.02985 (2019).
• 29. Chenxi Liu, Barret Zoph, Jonathon Shlens, Wei Hua, Li-Jia Li, Li Fei-Fei, Alan Yuille, Jonathan Huang, and Kevin Murphy. 2017b. Progressive Neural Architecture Search. In European Conference on Computer Vision .
• 30. Hanxiao Liu, Karen Simonyan, Oriol Vinyals, Chrisantha Fernando, and Koray Kavukcuoglu. 2017a. Hierarchical Representations for Efficient Architecture Search. ArXiv Preprint ArXiv:1711.00436 (2017).
• 31. Hanxiao Liu, Karen Simonyan, and Yiming Yang. 2018. Darts: Differentiable Architecture Search. ArXiv Preprint ArXiv:1806.09055 (2018).
• 32. Wei Liu, Dragomir Anguelov, Dumitru Erhan, Christian Szegedy, Scott Reed, Cheng-Yang Fu, and Alexander C Berg. 2016. Ssd: Single Shot Multibox Detector. In European Conference on Computer Vision .
• 33. Renqian Luo, Fei Tian, Tao Qin, Enhong Chen, and Tie-Yan Liu. 2018. Neural Architecture Optimization. In Advances in Neural Information Processing Systems .
• 34. Hiroshi Maehara. 2013. Euclidean Embeddings of Finite Metric Spaces. Discrete Mathematics (2013).
• 35. Randal S. Olson, Nathan Bartley, Ryan J. Urbanowicz, and Jason H. Moore. 2016. Evaluation of a Tree-based Pipeline Optimization Tool for Automating Data Science. In Genetic and Evolutionary Computation Conference 2016.
• 36. Fabian Pedregosa, Gaël Varoquaux, Alexandre Gramfort, Vincent Michel, Bertrand Thirion, Olivier Grisel, Mathieu Blondel, Peter Prettenhofer, Ron Weiss, Vincent Dubourg, Et Almbox. 2011. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research (2011).
• 37. Hieu Pham, Melody Y Guan, Barret Zoph, Quoc V Le, and Jeff Dean. 2018. Efficient Neural Architecture Search via Parameter Sharing. ArXiv Preprint ArXiv:1802.03268 (2018).
• 38. Esteban Real, Alok Aggarwal, Yanping Huang, and Quoc V Le. 2018. Regularized Evolution for Image Classifier Architecture Search. ArXiv Preprint ArXiv:1802.01548 (2018).
• 39. Esteban Real, Sherry Moore, Andrew Selle, Saurabh Saxena, Yutaka Leon Suematsu, Quoc Le, and Alex Kurakin. 2017. Large-scale Evolution of Image Classifiers, In: Proceedings of The International Conference on Machine Learning. ArXiv Preprint ArXiv:1703.01041 .
• 40. Jasper Snoek, Hugo Larochelle, and Ryan P Adams. 2012. Practical Bayesian Optimization of Machine Learning Algorithms. In Advances in Neural Information Processing Systems .
• 41. Masanori Suganuma, Shinichi Shirakawa, and Tomoharu Nagao. 2017. A Genetic Programming Approach to Designing Convolutional Neural Network Architectures. In Genetic and Evolutionary Computation Conference .
• 42. Mingxing Tan, Bo Chen, Ruoming Pang, Vijay Vasudevan, and Quoc V Le. 2018. Mnasnet: Platform-aware Neural Architecture Search for Mobile. ArXiv Preprint ArXiv:1807.11626 (2018).
• 43. Qiaoyu Tan, Ninghao Liu, and Xia Hu. 2019. Deep Representation Learning for Social Network Analysis. ArXiv Preprint ArXiv:1904.08547 (2019).
• 44. Chris Thornton, Frank Hutter, Holger H Hoos, and Kevin Leyton-Brown. 2013. Auto-WEKA: Combined Selection and Hyperparameter Optimization of Classification Algorithms. In: Proceedings of The International Conference on Knowledge Discovery and Data Mining .
• 45. Tao Wei, Changhu Wang, Yong Rui, and Chang Wen Chen. 2016. Network Morphism. In: Proceedings of The International Conference on Machine Learning .
• 46. Han Xiao, Kashif Rasul, and Roland Vollgraf. 2017. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. Showeprint[arXiv]cs.LG/cs.LG/1708.07747
• 47. Sirui Xie, Hehui Zheng, Chunxiao Liu, and Liang Lin. 2019. SNAS: Stochastic Neural Architecture Search. In: Proceedings of The International Conference on Learning Representations .
• 48. Pinar Yanardag and SVN Vishwanathan. 2015. Deep Graph Kernels. In: Proceedings of The International Conference on Knowledge Discovery and Data Mining .
• 49. Zhiping Zeng, Anthony KH. Tung, Jianyong Wang, Jianhua Feng, and Lizhu Zhou. 2009. Comparing Stars: On Approximating Graph Edit Distance. In: Proceedings of The International Conference on Very Large Data Bases .
• 50. Zhao Zhong, Junjie Yan, and Cheng-Lin Liu. 2017. Practical Network Blocks Design with Q-Learning. ArXiv Preprint ArXiv:1708.05552 (2017).
• 51. Barret Zoph and Quoc V Le. 2016. Neural Architecture Search with Reinforcement Learning. In: Proceedings of The International Conference on Learning Representations .

---

;

	Author	volume	Date Value	title	type	journal	titleUrl	doi	note	year
2019 AutoKerasAnEfficientNeuralArchi	Xia Hu Haifeng Jin Qingquan Song			Auto-Keras: An Efficient Neural Architecture Search System				10.1145/3292500.3330648		2019