Conditional Random Fields (CRFs) Model Family
A Conditional Random Fields (CRFs) Model Family is a discriminative undirected conditional graphical model family with jointly distributed random variables [math]\displaystyle{ \bf{X} }[/math] and [math]\displaystyle{ \bf{Y} }[/math], where [math]\displaystyle{ \bf{X} }[/math] are observed variables (covariates), and [math]\displaystyle{ \bf{Y} }[/math] are unobserved variables that are globally conditioned on [math]\displaystyle{ \bf{X} }[/math].
- Context:
- It was (largely) exposed in (Lafferty et al., 2001).
- It can be instantiated as a CRF Model Instance by a CRF Modeling Task (typically solved by a CRF training system that applies a CRF training algorithm).
- It can range from being a Hidden CRF Model to being a Nonhidden CRF Model.
- It can use a Log-Likelihood Loss Function.
- It can range, based on its Probabilistic Network Structure, from being a Linear-Chain CRF Metamodel to being a Non-Linear CRF Metamodel.
- It has a more relaxed Independence Assumptions than HMMs.
- It can range from being a Low-Order CRF, a High-Order CRF, to being a Semi-Markov CRF.
- It can be, based on ???, a Bayesian Conditional Random Fields (Qi, 2005)
- Example(s):
- Counter-Example(s):
- See: CRF Inferencing Task, Exponential Statistical Model, Discriminative Statistical Model.
References
2018
- http://wikipedia.org/wiki/Conditional_random_field#Description
- Lafferty, McCallum and Pereira define a CRF on observations [math]\displaystyle{ \boldsymbol{X} }[/math] and random variables [math]\displaystyle{ \boldsymbol{Y} }[/math] as follows:
Let [math]\displaystyle{ G = (V , E) }[/math] be a graph such that [math]\displaystyle{ \boldsymbol{Y} = (\boldsymbol{Y}_v)_{v\in V} }[/math], so that [math]\displaystyle{ \boldsymbol{Y} }[/math] is indexed by the vertices of [math]\displaystyle{ G }[/math].
Then [math]\displaystyle{ (\boldsymbol{X}, \boldsymbol{Y}) }[/math] is a conditional random field when the random variables [math]\displaystyle{ \boldsymbol{Y}_v }[/math], conditioned on [math]\displaystyle{ \boldsymbol{X} }[/math], obey the Markov property with respect to the graph: [math]\displaystyle{ p(\boldsymbol{Y}_v |\boldsymbol{X}, \boldsymbol{Y}_w, w \neq v) = p(\boldsymbol{Y}_v |\boldsymbol{X}, \boldsymbol{Y}_w, w \sim v) }[/math], where [math]\displaystyle{ \mathit{w} \sim v }[/math] means that [math]\displaystyle{ w }[/math] and [math]\displaystyle{ v }[/math] are neighbors in [math]\displaystyle{ G }[/math].
What this means is that a CRF is an undirected graphical model whose nodes can be divided into exactly two disjoint sets [math]\displaystyle{ \boldsymbol{X} }[/math] and [math]\displaystyle{ \boldsymbol{Y} }[/math], the observed and output variables, respectively; the conditional distribution [math]\displaystyle{ p(\boldsymbol{Y}|\boldsymbol{X}) }[/math] is then modeled.
- Lafferty, McCallum and Pereira define a CRF on observations [math]\displaystyle{ \boldsymbol{X} }[/math] and random variables [math]\displaystyle{ \boldsymbol{Y} }[/math] as follows:
2015
- (Huang, Xu & Yu, 2015) ⇒ Zhiheng Huang, Wei Xu, Kai Yu (2015). "Bidirectional LSTM-CRF models for sequence tagging (PDF)". arXiv preprint arXiv:1508.01991.
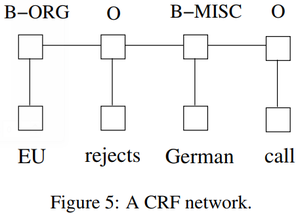
- QUOTE: There are two different ways to make use of neighbor tag information in predicting current tags. The first is to predict a distribution of tags for each time step and then use beam-like decoding to find optimal tag sequences. The work of maximum entropy classifier (Ratnaparkhi, 1996) and Maximum entropy Markov models (MEMMs) (McCallum et al., 2000) fall in this category. The second one is to focus on sentence level instead of individual positions, thus leading to Conditional Random Fields (CRF) models (Lafferty et al., 2001) (Fig. 5). Note that the inputs and outputs are directly connected, as opposed to LSTM and bidirectional LSTM networks where memory cells/recurrent components are employed. It has been shown that CRFs can produce higher tagging accuracy in general.
.
- QUOTE: There are two different ways to make use of neighbor tag information in predicting current tags. The first is to predict a distribution of tags for each time step and then use beam-like decoding to find optimal tag sequences. The work of maximum entropy classifier (Ratnaparkhi, 1996) and Maximum entropy Markov models (MEMMs) (McCallum et al., 2000) fall in this category. The second one is to focus on sentence level instead of individual positions, thus leading to Conditional Random Fields (CRF) models (Lafferty et al., 2001) (Fig. 5). Note that the inputs and outputs are directly connected, as opposed to LSTM and bidirectional LSTM networks where memory cells/recurrent components are employed. It has been shown that CRFs can produce higher tagging accuracy in general.
2013
- http://en.wikipedia.org/wiki/Conditional_random_field#Description
- Conditional random fields (CRFs) are a class of statistical modelling method often applied in pattern recognition and machine learning, where they are used for structured prediction. Whereas an ordinary classifier predicts a label for a single sample without regard to "neighboring" samples, a CRF can take context into account; e.g., the linear chain CRF popular in natural language processing predicts sequences of labels for sequences of input samples.
CRFs are a type of discriminative undirected probabilistic graphical model. It is used to encode known relationships between observations and construct consistent interpretations. It is often used for labeling or parsing of sequential data, such as natural language text or biological sequences[1] and in computer vision.[2] Specifically, CRFs find applications in shallow parsing,[3] named entity recognition[4] and gene finding, among other tasks, being an alternative to the related hidden Markov models. In computer vision, CRFs are often used for object recognition and image segmentation.
- Conditional random fields (CRFs) are a class of statistical modelling method often applied in pattern recognition and machine learning, where they are used for structured prediction. Whereas an ordinary classifier predicts a label for a single sample without regard to "neighboring" samples, a CRF can take context into account; e.g., the linear chain CRF popular in natural language processing predicts sequences of labels for sequences of input samples.
2012
- (Wikipedia, 2012) ⇒ http://en.wikipedia.org/wiki/Conditional_random_field
- … a CRF is an undirected graphical model whose nodes can be divided into exactly two disjoint sets [math]\displaystyle{ \boldsymbol{X} }[/math] and [math]\displaystyle{ \boldsymbol{Y} }[/math], the observed and output variables, respectively; the conditional distribution [math]\displaystyle{ p(\boldsymbol{Y}|\boldsymbol{X}) }[/math] is then modeled. The Markov property means that for any pair of nodes [math]\displaystyle{ v, \lt math\gt w }[/math] \in \boldsymbol{Y}</math> there exists a single neighbour [math]\displaystyle{ w' }[/math] of [math]\displaystyle{ v }[/math] such that [math]\displaystyle{ v }[/math] is conditionally independent of [math]\displaystyle{ w }[/math], given [math]\displaystyle{ w' }[/math] and [math]\displaystyle{ \boldsymbol{X} }[/math]. This means that the graphical structure of [math]\displaystyle{ \boldsymbol{Y} }[/math] (ignoring [math]\displaystyle{ \boldsymbol{X} }[/math]) has to be cycle-free, and is tree-structured by definition. Given the tree-structure of the output graph, [math]\displaystyle{ p(\boldsymbol{Y}|\boldsymbol{X})\propto\exp\left(\sum_{v\in V,k}\lambda_kf_k(v, \boldsymbol{Y}_v, \boldsymbol{X}) + \sum_{e\in E,l}\mu_lg_l(e,\boldsymbol{Y}|_e, \boldsymbol{X})\right) }[/math] where [math]\displaystyle{ \boldsymbol{Y}|_e }[/math] is the two endpoints of the edge [math]\displaystyle{ e }[/math], according to the Hammersley–Clifford theorem. As opposed to a general undirected model, parameter estimation and exact inference are both tractable in this kind of model.
For general graphs, the problem of exact inference in CRFs is intractable. The inference problem for a CRF is basically the same as for an MRF and the same arguments hold. For graphs with chain or tree structure, exact inference is possible. The algorithms used in these cases are analogous to the forward-backward and Viterbi algorithm for the case of HMMs.
Learning the parameters [math]\displaystyle{ \theta }[/math] is usually done by maximum likelihood learning for [math]\displaystyle{ p(Y_i|X_i; \theta) }[/math]. If all nodes have exponential family distributions and all nodes are observed during training, this optimization is convex. It can be solved for example using gradient descent algorithms Quasi-Newton methods, such as the L-BFGS algorithm. On the other hand, if some variables are unobserved, the inference problem has to be solved for these variables. This is intractable to do exact in general graphs, so approximations have to be used.
- … a CRF is an undirected graphical model whose nodes can be divided into exactly two disjoint sets [math]\displaystyle{ \boldsymbol{X} }[/math] and [math]\displaystyle{ \boldsymbol{Y} }[/math], the observed and output variables, respectively; the conditional distribution [math]\displaystyle{ p(\boldsymbol{Y}|\boldsymbol{X}) }[/math] is then modeled. The Markov property means that for any pair of nodes [math]\displaystyle{ v, \lt math\gt w }[/math] \in \boldsymbol{Y}</math> there exists a single neighbour [math]\displaystyle{ w' }[/math] of [math]\displaystyle{ v }[/math] such that [math]\displaystyle{ v }[/math] is conditionally independent of [math]\displaystyle{ w }[/math], given [math]\displaystyle{ w' }[/math] and [math]\displaystyle{ \boldsymbol{X} }[/math]. This means that the graphical structure of [math]\displaystyle{ \boldsymbol{Y} }[/math] (ignoring [math]\displaystyle{ \boldsymbol{X} }[/math]) has to be cycle-free, and is tree-structured by definition. Given the tree-structure of the output graph, [math]\displaystyle{ p(\boldsymbol{Y}|\boldsymbol{X})\propto\exp\left(\sum_{v\in V,k}\lambda_kf_k(v, \boldsymbol{Y}_v, \boldsymbol{X}) + \sum_{e\in E,l}\mu_lg_l(e,\boldsymbol{Y}|_e, \boldsymbol{X})\right) }[/math] where [math]\displaystyle{ \boldsymbol{Y}|_e }[/math] is the two endpoints of the edge [math]\displaystyle{ e }[/math], according to the Hammersley–Clifford theorem. As opposed to a general undirected model, parameter estimation and exact inference are both tractable in this kind of model.
2012b
- (Barber, 2012) ⇒ David Barber. (2012). “Bayesian Reasoning and Machine Learning.” In: Cambridge University Press. ISBN: 0521518148, 9780521518147.
- QUOTE: CRFs can also be viewed simply as Markov networks with exponential form potentials, as in section(9.6.4).
2011
- (Sammut & Webb, 2011) ⇒ Claude Sammut (editor), and Geoffrey I. Webb (editor). (2011). “Conditional Random Field.” In: (Sammut & Webb, 2011) p.208
2009
- http://www.inference.phy.cam.ac.uk/hmw26/crf/
- QUOTE: Conditional random fields (CRFs) are a probabilistic framework for labeling and segmenting structured data, such as sequences, trees and lattices. The underlying idea is that of defining a conditional probability distribution over label sequences given a particular observation sequence, rather than a joint distribution over both label and observation sequences. The primary advantage of CRFs over hidden Markov models is their conditional nature, resulting in the relaxation of the independence assumptions required by HMMs in order to ensure tractable inference. Additionally, CRFs avoid the label bias problem, a weakness exhibited by maximum entropy Markov models (MEMMs) and other conditional Markov models based on directed graphical models. CRFs outperform both MEMMs and HMMs on a number of real-world tasks in many fields, including bioinformatics, computational linguistics and speech recognition.
2008
- (Pereira, 2008) ⇒ Fernando Pereira's Homepage http://www.cis.upenn.edu/~pereira/
- QUOTE: Many sequence-processing problems involve breaking it into subsequences (person name vs other), or labeling sequence elements (parts of speech). Higher-level analyses involve parsing the sequence into a tree or graph representing its hierarchical structure. Previous approaches using probabilistic generative models like HMMs and PCFGs have difficulty in dealing with correlated features of the input sequence. We have been developing and applying structured linear models, starting with conditional random fields, as a more flexible, effective approach to learning how to segment and parse sequences."
2007
- (Klinger & Tomanek, 2007) ⇒ Roman Klinger, and Katrin Tomanek. (2007). “Classical Probabilistic Models and Conditional Random Fields." Algorithm Engineering Report TR07-2-013, Department of Computer Science, Dortmund University of Technology, December (2007). ISSN 1864-4503.
2007b
- (Sutton & McCallum, 2007) ⇒ Charles Sutton, and Andrew McCallum. (2007). “An Introduction to Conditional Random Fields for Relational Learning.” In: (Getoor & Taskar, 2007).
- QUOTE: Let [math]\displaystyle{ G }[/math] be a factor graph over [math]\displaystyle{ Y }[/math] . Then [math]\displaystyle{ p(y|x) }[/math] is a conditional random field if for any fixed [math]\displaystyle{ x }[/math], the distribution [math]\displaystyle{ \it{p}(\bf{y}|\bf{x}) }[/math] factorizes according to [math]\displaystyle{ \it{G} }[/math]. Thus, every conditional distribution [math]\displaystyle{ \it{p}(\bf{y} \vert \bf{x}) }[/math] is a CRF for some, perhaps trivial, factor graph. If [math]\displaystyle{ F = {Ψ_A} }[/math] is the set of factors in [math]\displaystyle{ G }[/math], and each factor takes the exponential family form (1.3), then the conditional distribution can be written as
 In addition, practical models rely extensively on parameter tying. For example, in the linear-chain case, often the same weights are used for the factors t(yt, yt−1, xt) at each time step. To denote this, we partition the factors of G into C = {C1,C2, . . .CP }, where each Cp is a clique template whose parameters are tied. This notion of clique template generalizes that in Taskar et al. [2002], Sutton et al. [2004], and Richardson and Domingos [2005]. Each clique template Cp is a set of factors which has a corresponding set of sufficient statistics {fpk(xp, yp)} and parameters p 2 <K(p). Then the CRF can be written as
In addition, practical models rely extensively on parameter tying. For example, in the linear-chain case, often the same weights are used for the factors t(yt, yt−1, xt) at each time step. To denote this, we partition the factors of G into C = {C1,C2, . . .CP }, where each Cp is a clique template whose parameters are tied. This notion of clique template generalizes that in Taskar et al. [2002], Sutton et al. [2004], and Richardson and Domingos [2005]. Each clique template Cp is a set of factors which has a corresponding set of sufficient statistics {fpk(xp, yp)} and parameters p 2 <K(p). Then the CRF can be written as 
… A conditional random field is simply a conditional distribution p(y|x) with an associated graphical structure. Because the model is conditional, dependencies among the input variables x do not need to be explicitly represented, affording the use of rich, global features of the input. … We will occasionally use the term random field to refer to a particular distribution among those defined by an undirected model. To reiterate, we will consistently use the term model to refer to a family of distributions, and random field (or more commonly, distribution) to refer to a single one. ...

Figure 1.2 Diagram of the relationship between naive Bayes, logistic regression, HMMs, linear-chain CRFs, generative models, and general CRFs.
- QUOTE: Let [math]\displaystyle{ G }[/math] be a factor graph over [math]\displaystyle{ Y }[/math] . Then [math]\displaystyle{ p(y|x) }[/math] is a conditional random field if for any fixed [math]\displaystyle{ x }[/math], the distribution [math]\displaystyle{ \it{p}(\bf{y}|\bf{x}) }[/math] factorizes according to [math]\displaystyle{ \it{G} }[/math]. Thus, every conditional distribution [math]\displaystyle{ \it{p}(\bf{y} \vert \bf{x}) }[/math] is a CRF for some, perhaps trivial, factor graph. If [math]\displaystyle{ F = {Ψ_A} }[/math] is the set of factors in [math]\displaystyle{ G }[/math], and each factor takes the exponential family form (1.3), then the conditional distribution can be written as
2006
- (Tasi et al., 2006) ⇒ Tzong-han Tsai, Wen-Chi Chou, Shih-Hung Wu, Ting-Yi Sung, Jieh Hsiang, and Wen-Lian Hsu. (2006). “Integrating Linguistic Knowledge into a Conditional Random Field Framework to Identify Biomedical Named Entities.” In: Expert Systems with Applications: An International Journal, 30(1). doi:10.1016/j.eswa.2005.09.072
- QUOTE: Conditional random fields (Lafferty, McCallum, & Pereira, 2001) (CRF) are probabilistic frameworks for labeling and segmenting sequential data. They are probabilistic tagging models that provide the conditional probability of a possible tag sequence [math]\displaystyle{ \boldsymbol{y} = y_1,y_2,...,y_n }[/math] given the input token sequence [math]\displaystyle{ \boldsymbol{x} = x_1,x_2,...,x_n }[/math]. We use two random variables [math]\displaystyle{ \boldsymbol{X} }[/math] and [math]\displaystyle{ \boldsymbol{Y} }[/math] to denote any input token sequences and tag sequences, respectively.
A CRF on ([math]\displaystyle{ \boldsymbol{X}, \boldsymbol{Y} }[/math]) is specified by a vector [math]\displaystyle{ \boldsymbol{f} }[/math] of local features and a corresponding weight vector [math]\displaystyle{ \boldsymbol{\lambda} }[/math]. There are two kinds of local features: the state feature [math]\displaystyle{ \boldsymbol{s}(y_i, \boldsymbol{x}, i) }[/math] and the transition feature [math]\displaystyle{ \boldsymbol{f}(y_{i-1}, y_i, \boldsymbol{x}, i) }[/math], where [math]\displaystyle{ y_{i-1} }[/math] and [math]\displaystyle{ y_i }[/math] are tags at positions [math]\displaystyle{ i-1 }[/math] and [math]\displaystyle{ i }[/math] in the tag sequence, respectively; [math]\displaystyle{ i }[/math] is the input position. Each dimension of a feature vector is a distinct function. When defining feature functions, we construct a set of real-valued features [math]\displaystyle{ \boldsymbol{b}(\boldsymbol{x}, i) }[/math] of the observation to express some characteristic of the empirical distribution of the training data that should also hold true of the model distribution.
- QUOTE: Conditional random fields (Lafferty, McCallum, & Pereira, 2001) (CRF) are probabilistic frameworks for labeling and segmenting sequential data. They are probabilistic tagging models that provide the conditional probability of a possible tag sequence [math]\displaystyle{ \boldsymbol{y} = y_1,y_2,...,y_n }[/math] given the input token sequence [math]\displaystyle{ \boldsymbol{x} = x_1,x_2,...,x_n }[/math]. We use two random variables [math]\displaystyle{ \boldsymbol{X} }[/math] and [math]\displaystyle{ \boldsymbol{Y} }[/math] to denote any input token sequences and tag sequences, respectively.
2006b
- (Culotta et al., 2006) ⇒ Aron Culotta, Andrew McCallum, and Jonathan Betz. (2006). “Integrating Probabilistic Extraction Models and Data Mining to Discover Relations and Patterns in Text.” In: Proceedings of HLT-NAACL 2006.
2005
- (Wallach, 2005) ⇒ Hanna M. Wallach. (2005). “Conditional Random Fields." Literature Survey Webpage.
- Conditional random fields (CRFs) are a probabilistic framework for labeling and segmenting structured data, such as sequences, trees and lattices. The underlying idea is that of defining a conditional probability distribution over label sequences given a particular observation sequence, rather than a joint distribution over both label and observation sequences. The primary advantage of CRFs over hidden Markov models is their conditional nature, resulting in the relaxation of the independence assumptions required by HMMs in order to ensure tractable inference. Additionally, CRFs avoid the label bias problem, a weakness exhibited by maximum entropy Markov models (MEMMs) and other conditional Markov models based on directed graphical models. CRFs outperform both MEMMs and HMMs on a number of real-world tasks in many fields, including bioinformatics, computational linguistics and speech recognition.
2005b
- (Jie Tang, 2005) ⇒ Jie Tang. (2005). “An Introduction for Conditional Random Fields." Literature Survey ¨C 2, Dec, 2005, at Tsinghua.
- CRF is a Markov Random Fields. By the Hammersley-Clifford theorem, the probability of a label can be expressed as a Gibbs distribution, so that
 In labeling, the task is to find the label sequence that has the largest probability. Then the key is to estimate the parameter lambda
In labeling, the task is to find the label sequence that has the largest probability. Then the key is to estimate the parameter lambda 
- CRF is a Markov Random Fields. By the Hammersley-Clifford theorem, the probability of a label can be expressed as a Gibbs distribution, so that
2004
- http://crf.sourceforge.net/introduction/models.html
- (McDonald et al., 2004) ⇒ Ryan T. McDonald, R. Scott Winters, Mark Mandel, Yang Jin, Peter S. White, and Fernando Pereira. (2004). “An entity tagger for recognizing acquired genomic variations in cancer literature." Bioinformatics 2004 20(17). doi:10.1093/bioinformatics/bth350.
- QUOTE: These models are convenient because they allow us to combine the effects of many potentially informative features and have previously been successfully used for other biomedical named entity taggers (McDonald and Pereira, 2004).
CRFs model the conditional probability of a tag sequence given an observation sequence: P(T|O) where O is an observation sequence, in our case a sequence of tokens in the abstract, and T=t1,t2,...,tn is a corresponding tag sequence in which each tab labels the corresponding token with on of TYPE, LOCATION, INITIAL-STATE, ALTERED-STATE and OTHER. CRFs are log-linear models based on a set of feature functions, fi(tj,tj-1,O) that map predicates on observation/tag-transition pairs to binary values.
Each feature has an associated weight, li, that measure its effect on the overall choice of tags.
These models are convenient because they allow us to combine the effects of many potentially informative features.
Given a trained model, the optimal tag sequence for new examples is found with the Viterbi algorithm (Rabiner, 1993).
- QUOTE: These models are convenient because they allow us to combine the effects of many potentially informative features and have previously been successfully used for other biomedical named entity taggers (McDonald and Pereira, 2004).
2004b
- (Wallach, 2004) ⇒ Wallach, 2004) ⇒ Hanna M. Wallach. (2004). “Conditional Random Fields: An introduction." Technical Report MS-CIS-04-21, University of Pennsylvania.
- Note: defines and applies a Linear-Chain Conditional Random Field.
2003a
- (Sha & Pereira, 2003a) ⇒ Fei Sha, and Fernando Pereira. (2003). “Shallow Parsing with Conditional Random Fields.” In: Proceedings of the 2003 Conference of the North American Chapter of the Association for Computational Linguistics on Human Language Technology (NAACL 2003). doi:10.3115/1073445.1073473
2003b
- (Zelenko et al., 2003) ⇒ Dmitry Zelenko, Chinatsu Aone, and Anthony Richardella. (2003). “Kernel Methods for Relation Extraction.” In: Journal of Machine Learning Research, 3.
- QUOTE: CRFs are an example of exponential models (Berger et al., 1996); as such, they enjoy a number of attractive properties (e.g., global likelihood maximum) and are better suited for modeling sequential data, as contrasted with other conditional models (Lafferty et al., 2001).
2003c
- (McCallum, 2003) ⇒ Andrew McCallum. (2003). “Efficiently Inducing Features of Conditional Random Fields.” In: Proceedings of the 19th Conference on Uncertainty in Artificial Intelligence.
2001
- (Lafferty et al., 2001) ⇒ John D. Lafferty, Andrew McCallum, and Fernando Pereira. (2001). “Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data.” In: Proceedings of ICML 2001.
- QUOTE: We present conditional random fields, a framework for building probabilistic models to segment and label sequence data. Conditional random fields offer several advantages over hidden Markov models and stochastic grammars for such tasks, including the ability to relax strong independence assumptions made in those models. Conditional random fields also avoid a fundamental limitation of maximum entropy Markov models (MEMMs) and other discriminative Markov models based on directed graphical models, which can be biased towards states with few successor states. We present iterative parameter estimation algorithms for conditional random fields and compare the performance of the resulting models to HMMs and MEMMs on synthetic and natural-language data.
… Definition: Let [math]\displaystyle{ G = (V,E) }[/math] be a graph such that [math]\displaystyle{ Y = (Y_v)_{v \in V} }[/math], so that Y is indexed by the vertices of [math]\displaystyle{ G }[/math]. Then [math]\displaystyle{ (X,Y) }[/math] is a conditional random field in case, when conditioned on X, the random variables [math]\displaystyle{ Y_v }[/math] obey the Markov property with respect to the graph: [math]\displaystyle{ p(Y_v \vert X,Y_w,w \neq v) = p(Y_v \vert X,Y_w, \lt math\gt w }[/math] \sim v)</math>, where w~v means that w and v are neighbors in G.
- QUOTE: We present conditional random fields, a framework for building probabilistic models to segment and label sequence data. Conditional random fields offer several advantages over hidden Markov models and stochastic grammars for such tasks, including the ability to relax strong independence assumptions made in those models. Conditional random fields also avoid a fundamental limitation of maximum entropy Markov models (MEMMs) and other discriminative Markov models based on directed graphical models, which can be biased towards states with few successor states. We present iterative parameter estimation algorithms for conditional random fields and compare the performance of the resulting models to HMMs and MEMMs on synthetic and natural-language data.