2014 DropoutASimpleWaytoPreventNeura

• (Srivastava et al., 2014) ⇒ Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. (2014). “Dropout: A Simple Way to Prevent Neural Networks from Overfitting.” In: The Journal of Machine Learning Research, 15(1).

Subject Headings: Dropout Algorithm.

Cited By

• Google Scholar: ~ 23,259 Citations, Retrieved:2020-10-18.
• ACM DL: ~ 1,299 Citations, Retrieved:2020-10-18.

Quotes

Abstract

Deep neural nets with a large number of parameters are very powerful machine learning systems. However, overfitting is a serious problem in such networks. Large networks are also slow to use, making it difficult to deal with overfitting by combining the predictions of many different large neural nets at test time. Dropout is a technique for addressing this problem. The key idea is to randomly drop units (along with their connections) from the neural network during training. This prevents units from co-adapting too much. During training, dropout samples from an exponential number of different "thinned" networks. At test time, it is easy to approximate the effect of averaging the predictions of all these thinned networks by simply using a single unthinned network that has smaller weights. This significantly reduces overfitting and gives major improvements over other regularization methods. We show that dropout improves the performance of neural networks on supervised learning tasks in vision, speech recognition, document classification and computational biology, obtaining state-of-the-art results on many benchmark data sets.

1. Introduction

Deep neural networks contain multiple non-linear hidden layers and this makes them very expressive models that can learn very complicated relationships between their inputs and outputs. With limited training data, however, many of these complicated relationships will be the result of sampling noise, so they will exist in the training set but not in real test data even if it is drawn from the same distribution. This leads to overfitting and many methods have been developed for reducing it. These include stopping the training as soon as performance on a validation set starts to get worse, introducing weight penalties of various kinds such as L1 and L2 regularization and soft weight sharing (Nowlan and Hinton, 1992).

With unlimited computation, the best way to "regularize" a fixed-sized model is to average the predictions of all possible settings of the parameters, weighting each setting by its posterior probability given the training data. This can sometimes be approximated quite well for simple or small models (Xiong et al., 2011; Salakhutdinov and Mnih, 2008), but we would like to approach the performance of the Bayesian gold standard using considerably less computation. We propose to do this by approximating an equally weighted geometric mean of the predictions of an exponential number of learned models that share parameters.

 Model combination nearly always improves the performance of machine learning methods. With large neural networks, however, the obvious idea of averaging the outputs of many separately trained nets is prohibitively expensive. Combining several models is most helpful when the individual models are different from each other and in order to make neural net models different, they should either have different architectures or be trained on different data. Training many different architectures is hard because finding optimal hyperparameters for each architecture is a daunting task and training each large network requires a lot of computation. Moreover, large networks normally require large amounts of training data and there may not be enough data available to train different networks on different subsets of the data. Even if one was able to train many different large networks, using them all at test time is infeasible in applications where it is important to respond quickly.

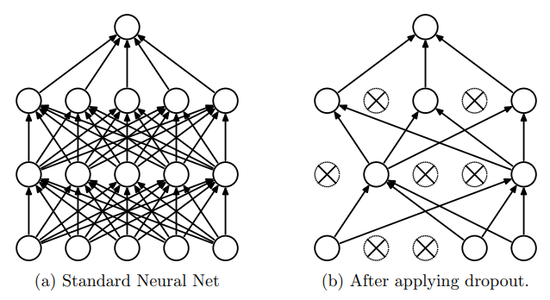
 Dropout is a technique that addresses both these issues. It prevents overfitting and provides a way of approximately combining exponentially many different neural network architectures efficiently. The term “dropout” refers to dropping out units (hidden and visible) in a neural network. By dropping a unit out, we mean temporarily removing it from the network, along with all its incoming and outgoing connections, as shown in Figure 1. The choice of which units to drop is random. In the simplest case, each unit is retained with a fixed probability $p$ independent of other units, where $p$ can be chosen using a validation set or can simply be set at 0.5, which seems to be close to optimal for a wide range of networks and tasks. For the input units, however, the optimal probability of retention is usually closer to 1 than to 0:5.

Figure 1: Dropout Neural Net Model. Left: A standard neural net with 2 hidden layers. Right: An example of a thinned net produced by applying dropout to the network on the left. Crossed units have been dropped.

Applying dropout to a neural network amounts to sampling a "thinned" network from it. The thinned network consists of all the units that survived dropout (Figure 1b). A neural net with $n$ units, can be seen as a collection of $2n$ possible thinned neural networks. These networks all share weights so that the total number of parameters is still $O(n2)$, or less. For each presentation of each training case, a new thinned network is sampled and trained. So training a neural network with dropout can be seen as training a collection of $2n$ thinned networks with extensive weight sharing, where each thinned network gets trained very rarely, if at all.

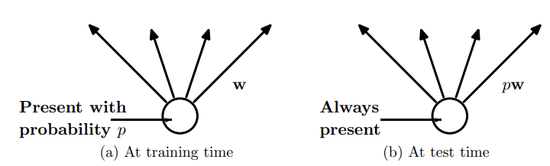
At test time, it is not feasible to explicitly average the predictions from exponentially many thinned models. However, a very simple approximate averaging method works well in practice. The idea is to use a single neural net at test time without dropout. The weights of this network are scaled-down versions of the trained weights. If a unit is retained with probability $p$ during training, the outgoing weights of that unit are multiplied by $p$ at test time as shown in Figure 2. This ensures that for any hidden unit the expected output (under the distribution used to drop units at training time) is the same as the actual output at test time. By doing this scaling, $2n$ networks with shared weights can be combined into a single neural network to be used at test time. We found that training a network with dropout and using this approximate averaging method at test time leads to significantly lower generalization error on a wide variety of classification problems compared to training with other regularization methods.

Figure 2: Left: A unit at training time that is present with probability $p$ and is connected to units in the next layer with weights $w$. Right: At test time, the unit is always present and the weights are multiplied by $p$. The output at test time is same as the expected output at training time.

This paper is structured as follows. Section 2 describes the motivation for this idea. Section 3 describes relevant previous work. Section 4 formally describes the dropout model. Section 5 gives an algorithm for training dropout networks. In Section 6, we present our experimental results where we apply dropout to problems in different domains and compare it with other forms of regularization and model combination. Section 7 analyzes the effect of dropout on different properties of a neural network and describes how dropout interacts with the network's hyperparameters. Section 8 describes the Dropout RBM model. In Section 9 we explore the idea of marginalizing dropout. In Appendix A we present a practical guide for training dropout nets. This includes a detailed analysis of the practical considerations involved in choosing hyperparameters when training dropout networks.

2. Motivation

A motivation for dropout comes from a theory of the role of sex in evolution (Livnat et al., 2010). Sexual reproduction involves taking half the genes of one parent and half of the other, adding a very small amount of random mutation, and combining them to produce an offspring. The asexual alternative is to create an offspring with a slightly mutated copy of the parent's genes. It seems plausible that asexual reproduction should be a better way to optimize individual fitness because a good set of genes that have come to work well together can be passed on directly to the offspring. On the other hand, sexual reproduction is likely to break up these co-adapted sets of genes, especially if these sets are large and, intuitively, this should decrease the fitness of organisms that have already evolved complicated co-adaptations. However, sexual reproduction is the way most advanced organisms evolved. One possible explanation for the superiority of sexual reproduction is that, over the long term, the criterion for natural selection may not be individual fitness but rather mix-ability of genes. The ability of a set of genes to be able to work well with another random set of genes makes them more robust. Since a gene cannot rely on a large set of partners to be present at all times, it must learn to do something useful on its own or in collaboration with a small number of other genes. According to this theory, the role of sexual reproduction is not just to allow useful new genes to spread throughout the population, but also to facilitate this process by reducing complex co-adaptations that would reduce the chance of a new gene improving the fitness of an individual. Similarly, each hidden unit in a neural network trained with dropout must learn to work with a randomly chosen sample of other units. This should make each hidden unit more robust and drive it towards creating useful features on its own without relying on other hidden units to correct its mistakes. However, the hidden units within a layer will still learn to do different things from each other. One might imagine that the net would become robust against dropout by making many copies of each hidden unit, but this is a poor solution for exactly the same reason as replica codes are a poor way to deal with a noisy channel.

A closely related, but slightly different motivation for dropout comes from thinking about successful conspiracies. Ten conspiracies each involving five people is probably a better way to create havoc than one big conspiracy that requires fifty people to all play their parts correctly. If conditions do not change and there is plenty of time for rehearsal, a big conspiracy can work well, but with non-stationary conditions, the smaller the conspiracy the greater its chance of still working. Complex co-adaptations can be trained to work well on a training set, but on novel test data they are far more likely to fail than multiple simpler co-adaptations that achieve the same thing.

3. Related Work

Dropout can be interpreted as a way of regularizing a neural network by adding noise to its hidden units. The idea of adding noise to the states of units has previously been used in the context of Denoising Autoencoders (DAEs) by Vincent et al. (2008, 2010) where noise is added to the input units of an autoencoder and the network is trained to reconstruct the noise-free input. Our work extends this idea by showing that dropout can be effectively applied in the hidden layers as well and that it can be interpreted as a form of model averaging. We also show that adding noise is not only useful for unsupervised feature learning but can also be extended to supervised learning problems. In fact, our method can be applied to other neuron-based architectures, for example, Boltzmann Machines. While 5% noise typically works best for DAEs, we found that our weight scaling procedure applied at test time enables us to use much higher noise levels. Dropping out 20% of the input units and 50% of the hidden units was often found to be optimal.

Since dropout can be seen as a stochastic regularization technique, it is natural to consider its deterministic counterpart which is obtained by marginalizing out the noise. In this paper, we show that, in simple cases, dropout can be analytically marginalized out to obtain deterministic regularization methods. Recently, van der Maaten et al. (2013) also explored deterministic regularizers corresponding to different exponential-family noise distributions, including dropout (which they refer to as “blankout noise"). However, they apply noise to the inputs and only explore models with no hidden layers. Wang and Manning (2013) proposed a method for speeding up dropout by marginalizing dropout noise. Chen et al. (2012) explored marginalization in the context of denoising autoencoders.

In dropout, we minimize the loss function stochastically under a noise distribution. This can be seen as minimizing an expected loss function. Previous work of Globerson and Roweis (2006); Dekel et al. (2010) explored an alternate setting where the loss is minimized when an adversary gets to pick which units to drop. Here, instead of a noise distribution, the maximum number of units that can be dropped is fixed. However, this work also does not explore models with hidden units.

4. Model Description

This section describes the dropout neural network model. Consider a neural network with $L$ hidden layers. Let $l \in \{ 1, \cdots, L\}$ index the hidden layers of the network. Let $\mathbf{z}^{(l)}$ denote the vector of inputs into layer $l$, $\mathbf{y}^{(l)}$ denote the vector of outputs from layer $l$ ($\mathbf{y}^{(0)} = x$ is the input). $\mathbf{W^(l)}$ and $\mathbf{b}^{(l)}$ are the weights and biases at layer $l$. The feed-forward operation

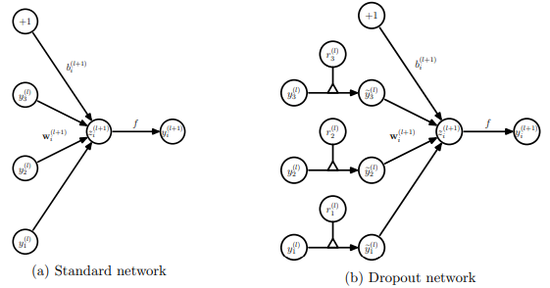
of a standard neural network (Figure 3a) can be described as (for $l \in \{0,\cdots,L-1\}$ and any hidden unit $i$)

$\begin{aligned} z_{i}^{(l+1)} &=\mathbf{w}_{i}^{(l+1)} \mathbf{y}^{l}+b_{i}^{(l+1)} \\ y_{i}^{(l+1)} &=f\left(z_{i}^{(l+1)}\right) \end{aligned}$

where $f$ is any activation function, for example, $f(x) = 1= (1 + exp(-x))$. With dropout, the feed-forward operation becomes (Figure 3b)

$\begin{aligned} r_{j}^{(l)} & \sim \text { Bernoulli }(p) \\ \tilde{\mathbf{y}}^{(l)} &=\mathbf{r}^{(l)} * \mathbf{y}^{(l)} \\ z_{i}^{(l+1)} &=\mathbf{w}_{i}^{(l+1)} \widetilde{\mathbf{y}}^{l}+b_{i}^{(l+1)} \\ y_{i}^{(l+1)} &=f\left(z_{i}^{(l+1)}\right) \end{aligned}$

Figure 3: Comparison of the basic operations of a standard and dropout network.

Here * denotes an element-wise product. For any layer $l$, $\mathbf{r}^{(l)}$ is a vector of independent Bernoulli random variables each of which has probability $p$ of being $1$. This vector is sampled and multiplied element-wise with the outputs of that layer, $y^{(l)}$, to create the thinned outputs $\tilde{y ^{(l)}}$. The thinned outputs are then used as input to the next layer. This process is applied at each layer. This amounts to sampling a sub-network from a larger network. For learning, the derivatives of the loss function are backpropagated through the sub-network. At test time, the weights are scaled as $W^{(l)}_{test} = pW^{(l)}$ as shown in Figure 2. The resulting neural network is used without dropout.

5. Learning Dropout Nets

This section describes a procedure for training dropout neural nets.

5.1 Backpropagation

Dropout neural networks can be trained using stochastic gradient descent in a manner similar to standard neural nets. The only difference is that for each training case in a mini-batch, we sample a thinned network by dropping out units. Forward and backpropagation for that training case are done only on this thinned network. The gradients for each parameter are averaged over the training cases in each mini-batch. Any training case which does not use a parameter contributes a gradient of zero for that parameter. Many methods have been used to improve stochastic gradient descent such as momentum, annealed learning rate s and L2 weight decay. Those were found to be useful for dropout neural networks as well.

One particular form of regularization was found to be especially useful for dropout - constraining the norm of the incoming weight vector at each hidden unit to be upper bounded by a fixed constant $c$. In other words, if $\mathbf{w}$ represents the vector of weights incident on any hidden unit, the neural network was optimized under the constraint $||\mathbf{w}||_2 \leq c$. This constraint was imposed during optimization by projecting $\mathbf{w}$ onto the surface of a ball of radius $c$, whenever $\mathbf{w}$ went out of it. This is also called max-norm regularization since it implies that the maximum value that the norm of any weight can take is $c$. The constant $c$ is a tunable hyperparameter, which is determined using a validation set. Max-norm regularization has been previously used in the context of collaborative filtering (Srebro and Shraibman, 2005). It typically improves the performance of stochastic gradient descent training of deep neural nets, even when no dropout is used.

Although dropout alone gives significant improvements, using dropout along with max-norm regularization, large decaying learning rates and high momentum provides a significant boost over just using dropout. A possible justification is that constraining weight vectors to lie inside a ball of fixed radius makes it possible to use a huge learning rate without the possibility of weights blowing up. The noise provided by dropout then allows the optimization process to explore different regions of the weight space that would have otherwise been dificult to reach. As the learning rate decays, the optimization takes shorter steps, thereby doing less exploration and eventually settles into a minimum.

5.2 Unsupervised Pretraining

Neural networks can be pretrained using stacks of RBMs (Hinton and Salakhutdinov, 2006), autoencoders (Vincent et al., 2010) or Deep Boltzmann Machines (Salakhutdinov and Hinton, 2009). Pretraining is an effective way of making use of unlabeled data. Pretraining followed by fine-tuning with backpropagation has been shown to give significant performance boosts over finetuning from random initializations in certain cases. Dropout can be applied to fine-tune nets that have been pretrained using these techniques. The pretraining procedure stays the same. The weights obtained from pretraining should be scaled up by a factor of $1/p$. This makes sure that for each unit, the expected output from it under random dropout will be the same as the output during pretraining. We were initially concerned that the stochastic nature of dropout might wipe out the information in the pretrained weights. This did happen when the learning rate s used during fine-tuning were comparable to the best learning rate s for randomly initialized nets. However, when the learning rate s were chosen to be smaller, the information in the pretrained weights seemed to be retained and we were able to get improvements in terms of the final generalization error compared to not using dropout when finetuning.

6. Experimental Results

We trained dropout neural networks for classification problems on data sets in different domains. We found that dropout improved generalization performance on all data sets compared to neural networks that did not use dropout. Table 1 gives a brief description of the data sets. The data sets are

• MNIST : A standard toy data set of handwritten digits.
• TIMIT : A standard speech benchmark for clean speech recognition.
• CIFAR-10 and CIFAR-100 : Tiny natural images (Krizhevsky, 2009).
• Street View House Numbers data set (SVHN) : Images of house numbers collected by Google Street View (Netzer et al., 2011).
• ImageNet : A large collection of natural images.
• Reuters-RCV1 : A collection of Reuters newswire articles.
• Alternative Splicing data set: RNA features for predicting alternative gene splicing (Xiong et al., 2011).

We chose a diverse set of data sets to demonstrate that dropout is a general technique for improving neural nets and is not specific to any particular application domain. In this section, we present some key results that show the effectiveness of dropout. A more detailed description of all the experiments and data sets is provided in Appendix B.

Table 1: Overview of the data sets used in this paper.

Data Set	Domain	Dimensionality	Training Set	Test Set
MNIST	Vision	784 (28 $\times$ 28 grayscale)	60K	10K
SVHN	Vision	3072 (32 $\times$ 32 color)	600K	26K
CIFAR-10/100	Vision	3072 (32 $\times$ 32 color)	60K	10K
ImageNet (ILSVRC-2012)	Vision	65536 (256 $\times$ 256 color)	1.2M	150K
TIMIT	Speech	2520 (120-dim, 21 frames)	1.1M frames	58K frames
Reuters-RCV1	Text	2000	200K	200K
Alternative Splicing	Genetics	1014	2932	733

6.1 Results on Image Data Sets

We used five image data sets to evaluate dropout - MNIST, SVHN, CIFAR-10, CIFAR-100 and ImageNet. These data sets include different image types and training set sizes. Models which achieve state-of-the-art results on all of these data sets use dropout.

6.1.1 MNIST

The MNIST data set consists of $28 \times 28$ pixel handwritten digit images. The task is to classify the images into 10 digit classes. Table 2 compares the performance of dropout with other techniques. The best performing neural networks for the permutation invariant setting that do not use dropout or unsupervised pretraining achieve an error of about 1.60% (Simard et al., 2003). With dropout the error reduces to 1.35%. Replacing logistic units with rectiffed linear units (ReLUs) (Jarrett et al., 2009) further reduces the error to 1.25%. Adding max-norm regularization again reduces it to 1.06%. Increasing the size of the network leads to better results. A neural net with 2 layers and 8192 units per layer gets down to 0.95% error. Note that this network has more than 65 million parameters and is being trained on a data set of size 60, 000. Training a network of this size to give good generalization error is very hard with standard regularization methods and early stopping. Dropout, on the other hand, prevents overfitting, even in this case. It does not even need early stopping. Goodfellow et al. (2013) showed that results can be further improved to 0.94% by replacing ReLU units with maxout units. All dropout nets use $p = 0.5$ for hidden units and $p = 0.8$ for input units. More experimental details can be found in Appendix B.1.

 Dropout nets pretrained with stacks of RBMs and Deep Boltzmann Machines also give improvements as shown in Table 2. DBM - pretrained dropout nets achieve a test error of 0.79% which is the best performance ever reported for the permutation invariant setting. We note that it possible to obtain better results by using 2-D spatial information and augmenting the training set with distorted versions of images from the standard training set. We demonstrate the effectiveness of dropout in that setting on more interesting data sets.

Table 2: Comparison of different models on MNIST.

Method	Unit Type	Architecture	Error%
Standard Neural Net (Simard et al., 2003)	Logistic	2 layers, 800 units	1.60
SVM Gaussian kernel	NA	NA	1.40
Dropout NN	Logistic	3 layers, 1024 units	1.35
Dropout NN	ReLU	3 layers, 1024 units	1.25
Dropout NN + max-norm constraint	ReLU	3 layers, 1024 units	1.06
Dropout NN + max-norm constraint	ReLU	3 layers, 2048 units	1.04
Dropout NN + max-norm constraint	ReLU	2 layers, 4096 units	1.01
Dropout NN + max-norm constraint	ReLU	2 layers, 8192 units	0.95
Dropout NN + max-norm constraint (Goodfellow et al., 2013)	Maxout	2 layers, ($5 \times 240$) units	0.94
DBN + finetuning (Hinton and Salakhutdinov, 2006)	Logistic	500-500-2000	1.18
DBM + finetuning (Salakhutdinov and Hinton, 2009)	Logistic	500-500-2000	0.96
DBN + dropout finetuning	Logistic	500-500-2000	0.92
DBM + dropout finetuning	Logistic	500-500-2000	0.79

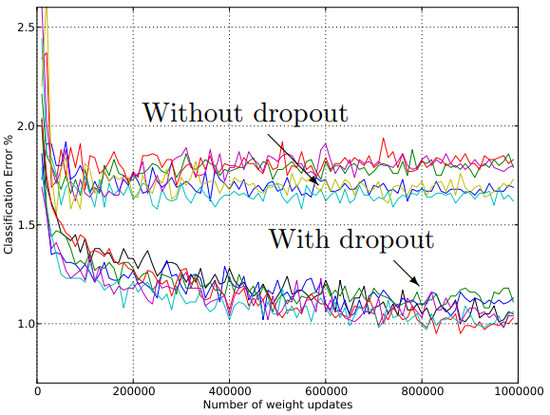
In order to test the robustness of dropout, classification experiments were done with networks of many different architectures keeping all hyperparameters, including $p$, fixed. Figure 4 shows the test error rates obtained for these different architectures as training progresses. The same architectures trained with and without dropout have drastically different test errors as seen as by the two separate clusters of trajectories. Dropout gives a huge improvement across all architectures, without using hyperparameters that were tuned specifically for each architecture.

Figure 4: Test error for different architectures with and without dropout. The networks have 2 to 4 hidden layers each with 1024 to 2048 units.

6.1.2 Street View House Numbers

The Street View House Numbers (SVHN) Data Set (Netzer et al., 2011) consists of color images of house numbers collected by Google Street View. Figure 5a shows some examples of images from this data set. The part of the data set that we use in our experiments consists of $32\times 32$ color images roughly centered on a digit in a house number. The task is to identify that digit.

For this data set, we applied dropout to convolutional neural networks (LeCun et al., 1989). The best architecture that we found has three convolutional layers followed by 2 fully connected hidden layers. All hidden units were ReLUs. Each convolutional layer was followed by a max-pooling layer. Appendix B.2 describes the architecture in more detail. Dropout was applied to all the layers of the network with the probability of retaining a hidden unit being $p = (0.9, 0.75, 0.75, 0.5, 0.5, 0:5)$ for the different layers of the network (going from input to convolutional layers to fully connected layers). Max-norm regularization was used for weights in both convolutional and fully connected layers. Table 3 compares the results obtained by different methods. We find that convolutional nets outperform other methods. The best performing convolutional nets that do not use dropout achieve an error rate of 3.95%. Adding dropout only to the fully connected layers reduces the error to 3.02%. Adding dropout to the convolutional layers as well further reduces the error to 2.55%. Even more gains can be obtained by using maxout units.

Table 3: Results on the Street View House Numbers data set.

Method	Error %
Binary Features (WDCH) (Netzer et al., 2011)	36.7
HOG (Netzer et al., 2011)	15.0
Stacked Sparse Autoencoders (Netzer et al., 2011)	10.3
KMeans (Netzer et al., 2011)	9.4
Multi-stage Conv Net with average pooling (Sermanet et al., 2012)	9.06
Multi-stage Conv Net + L2 pooling (Sermanet et al., 2012)	5.36
Multi-stage Conv Net + L4 pooling + padding (Sermanet et al., 2012)	4.90
Conv Net + max-pooling	3.95
Conv Net + max pooling + dropout in fully connected layers	3.02
Conv Net + stochastic pooling (Zeiler and Fergus, 2013)	2.80
Conv Net + max pooling + dropout in all layers	2.55
Conv Net + maxout (Goodfellow et al., 2013)	2.47
Human Performance	2.0

The additional gain in performance obtained by adding dropout in the convolutional layers (3.02% to 2.55%) is worth noting. One may have presumed that since the convolutional layers don't have a lot of parameters, overfitting is not a problem and therefore dropout would not have much effect. However, dropout in the lower layers still helps because it provides noisy inputs for the higher fully connected layers which prevents them from overfitting.

Figure 5: Samples from image data sets. Each row corresponds to a different category.

6.1.3 CIFAR-10 and CIFAR-100

The CIFAR-10 and CIFAR-100 data sets consist of $32 \times 32$ color images drawn from 10 and 100 categories respectively. Figure 5b shows some examples of images from this data set. A detailed description of the data sets, input preprocessing, network architectures and other experimental details is given in Appendix B.3. Table 4 shows the error rate obtained by different methods on these data sets. Without any data augmentation, Snoek et al. (2012) used Bayesian hyperparameter optimization to obtained an error rate of 14.98% on CIFAR-10. Using dropout in the fully connected layers reduces that to 14.32% and adding dropout in every layer further reduces the error to 12.61%. Goodfellow et al. (2013) showed that the error is further reduced to 11.68% by replacing ReLU units with maxout units. On CIFAR-100, dropout reduces the error from 43.48% to 37.20% which is a huge improvement. No data augmentation was used for either data set (apart from the input dropout).

Table 4: Error rates on CIFAR-10 and CIFAR-100.

Method	CIFAR-10	CIFAR-100
Conv Net + max pooling (hand tuned)	15.60	43.48
Conv Net + stochastic pooling (Zeiler and Fergus, 2013)	15.13	42.51
Conv Net + max pooling (Snoek et al., 2012)	14.98	-
Conv Net + max pooling + dropout fully connected layers	14.32	41.26
Conv Net + max pooling + dropout in all layers	12.61	37.20
Conv Net + maxout (Goodfellow et al., 2013)	11.68	38.57

6.1.4 ImageNet

ImageNet is a data set of over 15 million labeled high-resolution images belonging to roughly 22,000 categories. Starting in 2010, as part of the Pascal Visual Object Challenge, an annual competition called the ImageNet Large-Scale Visual Recognition Challenge (ILSVRC) has been held. A subset of ImageNet with roughly 1000 images in each of 1000 categories is used in this challenge. Since the number of categories is rather large, it is conventional to report two error rates: top-1 and top-5, where the top-5 error rate is the fraction of test images for which the correct label is not among the five labels considered most probable by the model. Figure 6 shows some predictions made by our model on a few test images.

 ILSVRC-2010 is the only version of ILSVRC for which the test set labels are available, so most of our experiments were performed on this data set. Table 5 compares the performance of different methods. Convolutional nets with dropout outperform other methods by a large margin. The architecture and implementation details are described in detail in Krizhevsky et al. (2012).

 Our model based on convolutional nets and dropout won the ILSVRC-2012 competition. Since the labels for the test set are not available, we report our results on the test set for the final submission and include the validation set results for different variations of our model. Table 6 shows the results from the competition. While the best methods based on standard vision features achieve a top-5 error rate of about 26%, convolutional nets with dropout achieve a test error of about 16% which is a staggering difference. Figure 6 shows some examples of predictions made by our model. We can see that the model makes very reasonable predictions, even when its best guess is not correct.

Figure 6: Some ImageNet test cases with the 4 most probable labels as predicted by our model. The length of the horizontal bars is proportional to the probability assigned to the labels by the model. Pink indicates ground truth.

Table 5: Results on the ILSVRC-2010 test set.

Model	Top-1	Top-5
Sparse Coding (Lin et al., 2010)	47.1	28.2
SIFT + Fisher Vectors (Sanchez and Perronnin, 2011)	45.7	25.7
Conv Net + dropout (Krizhevsky et al., 2012)	37.5	17.0

Table 6: Results on the ILSVRC-2012 validation/test set.

Model	Top-1 (val)	Top-5 (val)	Top-5 (test)
SVM on Fisher Vectors of Dense SIFT and Color Statistics	$-$	$-$	27.3
Avg of classiffers over FVs of SIFT, LBP, GIST and CSIFT	$-$	$-$	26.2
Conv Net + dropout (Krizhevsky et al., 2012)	40.7	18.2	$-$
Avg of 5 Conv Nets + dropout (Krizhevsky et al., 2012)	38.1	16.4	16.4

6.2 Results on TIMIT

Next, we applied dropout to a speech recognition task. We use the TIMIT data set which consists of recordings from 680 speakers covering 8 major dialects of American English reading ten phonetically-rich sentences in a controlled noise-free environment. Dropout neural networks were trained on windows of 21 log-filter bank frames to predict the label of the central frame. No speaker dependent operations were performed. Appendix B.4 describes the data preprocessing and training details. Table 7 compares dropout neural nets with other models. A 6-layer net gives a phone error rate of 23:4%. Dropout further improves it to 21.8%. We also trained dropout nets starting from pretrained weights. A 4-layer net pretrained with a stack of RBMs get a phone error rate of 22:7%. With dropout, this reduces to 19:7%. Similarly, for an 8-layer net the error reduces from 20.5% to 19.7%.

Table 7: Phone error rate on the TIMIT core test set.

Method	Phone Error Rate%
NN (6 layers) (Mohamed et al., 2010)	23.4
Dropout NN (6 layers)	21.8
DBN-pretrained NN (4 layers)	22.7
DBN-pretrained NN (6 layers) (Mohamed et al., 2010)	22.4
DBN-pretrained NN (8 layers) (Mohamed et al., 2010)	20.7
mcRBM-DBN-pretrained NN (5 layers) (Dahl et al., 2010)	20.5
DBN-pretrained NN (4 layers) + dropout	19.7
DBN-pretrained NN (8 layers) + dropout	19.7

6.3 Results on a Text Data Set

To test the usefulness of dropout in the text domain, we used dropout networks to train a document classiffer. We used a subset of the Reuters-RCV1 data set which is a collection of over 800,000 newswire articles from Reuters. These articles cover a variety of topics. The task is to take a bag of words representation of a document and classify it into 50 disjoint topics. Appendix B.5 describes the setup in more detail. Our best neural net which did not use dropout obtained an error rate of 31.05%. Adding dropout reduced the error to 29.62%. We found that the improvement was much smaller compared to that for the vision and speech data sets.

6.4 Comparison with Bayesian Neural Networks

Dropout can be seen as a way of doing an equally-weighted averaging of exponentially many models with shared weights. On the other hand, Bayesian neural networks (Neal, 1996) are the proper way of doing model averaging over the space of neural network structures and parameters. In dropout, each model is weighted equally, whereas in a Bayesian neural network each model is weighted taking into account the prior and how well the model fits the data, which is the more correct approach. Bayesian neural nets are extremely useful for solving problems in domains where data is scarce such as medical diagnosis, genetics, drug discovery and other computational biology applications. However, Bayesian neural nets are slow to train and diffcult to scale to very large network sizes. Besides, it is expensive to get predictions from many large nets at test time. On the other hand, dropout neural nets are much faster to train and use at test time. In this section, we report experiments that compare Bayesian neural nets with dropout neural nets on a small data set where Bayesian neural networks are known to perform well and obtain state-of-the-art results. The aim is to analyze how much does dropout lose compared to Bayesian neural nets. The data set that we use (Xiong et al., 2011) comes from the domain of genetics. The task is to predict the occurrence of alternative splicing based on RNA features. Alternative splicing is a significant cause of cellular diversity in mammalian tissues. Predicting the occurrence of alternate splicing in certain tissues under different conditions is important for understanding many human diseases. Given the RNA features, the task is to predict the probability of three splicing related events that biologists care about. The evaluation metric is Code Quality which is a measure of the negative KL divergence between the target and the predicted probability distributions (higher is better). Appendix B.6 includes a detailed description of the data set and this performance metric.

 Table 8 summarizes the performance of different models on this data set. Xiong et al. (2011) used Bayesian neural nets for this task. As expected, we found that Bayesian neural nets perform better than dropout. However, we see that dropout improves significantly upon the performance of standard neural nets and outperforms all other methods. The challenge in this data set is to prevent overfitting since the size of the training set is small. One way to prevent overfitting is to reduce the input dimensionality using PCA. Thereafter, standard techniques such as SVMs or logistic regression can be used. However, with dropout we were able to prevent overfitting without the need to do dimensionality reduction. The dropout nets are very large (1000s of hidden units) compared to a few tens of units in the Bayesian network. This shows that dropout has a strong regularizing effect.

Table 8: Results on the Alternative Splicing Data Set.

Method	Code Quality (bits)
Neural Network (early stopping) (Xiong et al., 2011)	440
Regression, PCA (Xiong et al., 2011)	463
SVM, PCA (Xiong et al., 2011)	487
Neural Network with dropout	567
Bayesian Neural Network (Xiong et al., 2011)	623

6.5 Comparison with Standard Regularizers

Several regularization methods have been proposed for preventing overfitting in neural networks. These include L2 weight decay (more generally Tikhonov regularization (Tikhonov, 1943)), lasso (Tibshirani, 1996), KL-sparsity and max-norm regularization. Dropout can be seen as another way of regularizing neural networks. In this section we compare dropout with some of these regularization methods using the MNIST data set. The same network architecture (784-1024-1024-2048-10) with ReLUs was trained using stochastic gradient descent with different regularizations. Table 9 shows the results. The values of different hyperparameters associated with each kind of regularization (decay constants, target sparsity, dropout rate, max-norm upper bound) were obtained using a validation set. We found that dropout combined with max-norm regularization gives the lowest generalization error.

Table 9: Comparison of different regularization methods on MNIST.

Method	Test Classification error %
L2	1.62
L2 + L1 applied towards the end of training	1.60
L2 + KL-sparsity	1.55
Max-norm	1.35
Dropout + L2	1.25
Dropout + Max-norm	1.05

7. Salient Features

The experiments described in the previous section provide strong evidence that dropout is a useful technique for improving neural networks. In this section, we closely examine how dropout affects a neural network. We analyze the effect of dropout on the quality of features produced. We see how dropout affects the sparsity of hidden unit activations. We also see how the advantages obtained from dropout vary with the probability of retaining units, size of the network and the size of the training set. These observations give some insight into why dropout works so well.

7.1 Effect on Features

In a standard neural network, the derivative received by each parameter tells it how it should change so the final loss function is reduced, given what all other units are doing. Therefore, units may change in a way that they fix up the mistakes of the other units. This may lead to complex co-adaptations. This in turn leads to overfitting because these co-adaptations do not generalize to unseen data. We hypothesize that for each hidden unit, dropout prevents co-adaptation by making the presence of other hidden units unreliable. Therefore, a hidden unit cannot rely on other specific units to correct its mistakes. It must perform well in a wide variety of different contexts provided by the other hidden units. To observe this effect directly, we look at the first level features learned by neural networks trained on visual tasks with and without dropout.

 Figure 7a shows features learned by an autoencoder on MNIST with a single hidden layer of 256 rectiffed linear units without dropout. Figure 7b shows the features learned by an identical autoencoder which used dropout in the hidden layer with p = 0.5. Both autoencoders had similar test reconstruction errors. However, it is apparent that the features shown in Figure 7a have co-adapted in order to produce good reconstructions. Each hidden unit on its own does not seem to be detecting a meaningful feature. On the other hand, in Figure 7b, the hidden units seem to detect edges, strokes and spots in different parts of the image. This shows that dropout does break up co-adaptations, which is probably the main reason why it leads to lower generalization errors.

Figure 7: Features learned on MNIST with one hidden layer autoencoders having 256 rectiffed linear units.

7.2 Effect on Sparsity

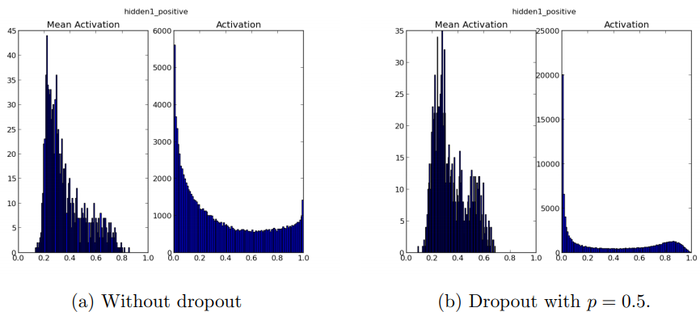
We found that as a side-effect of doing dropout, the activations of the hidden units become sparse, even when no sparsity inducing regularizers are present. Thus, dropout automatically leads to sparse representations. To observe this effect, we take the autoencoders trained in the previous section and look at the sparsity of hidden unit activations on a random mini-batch taken from the test set. Figure 8a and Figure 8b compare the sparsity for the two models. In a good sparse model, there should only be a few highly activated units for any data case. Moreover, the average activation of any unit across data cases should be low. To assess both of these qualities, we plot two histograms for each model. For each model, the histogram on the left shows the distribution of mean activations of hidden units across the minibatch. The histogram on the right shows the distribution of activations of the hidden units.

Comparing the histograms of activations we can see that fewer hidden units have high activations in Figure8b compared to Figure 8a, as seen by the significant mass away from zero for the net that does not use dropout. The mean activations are also smaller for the dropout net. The overall mean activation of hidden units is close to 2.0 for the autoencoder without dropout but drops to around 0.7 when dropout is used.

Figure 8: Effect of dropout on sparsity. ReLUs were used for both models. Left: The histogram of mean activations shows that most units have a mean activation of about 2.0. The histogram of activations shows a huge mode away from zero. Clearly, a large fraction of units have high activation. Right: The histogram of mean activations shows that most units have a smaller mean mean activation of about 0.7. The histogram of activations shows a sharp peak at zero. Very few units have high activation.

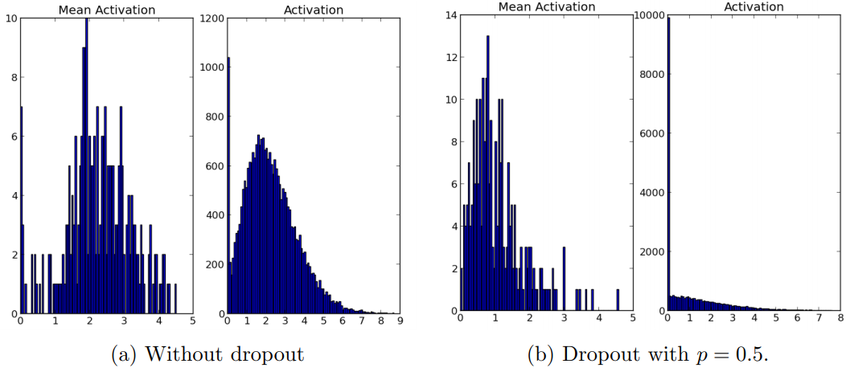
7.3 Effect of Dropout Rate

Dropout has a tunable hyperparameter $p$ (the probability of retaining a unit in the network). In this section, we explore the effect of varying this hyperparameter. The comparison is done in two situations.

1. The number of hidden units is held constant.

2. The number of hidden units is changed so that the expected number of hidden units that will be retained after dropout is held constant.

In the first case, we train the same network architecture with different amounts of dropout. We use a 784-2048-2048-2048-10 architecture. No input dropout was used. Figure 9a shows the test error obtained as a function of $p$. If the architecture is held constant, having a small $p$ means very few units will turn on during training. It can be seen that this has led to underfitting since the training error is also high. We see that as $p$ increases, the error goes down. It becomes at when $0.4 \leq p \leq 0.8$ and then increases as $p$ becomes close to 1.

Another interesting setting is the second case in which the quantity pn is held constant where $n$ is the number of hidden units in any particular layer. This means that networks that have small $p$ will have a large number of hidden units. Therefore, after applying dropout, the expected number of units that are present will be the same across different architectures. However, the test networks will be of different sizes. In our experiments, we set $pn = 256$ for the first two hidden layers and $pn = 512$ for the last hidden layer. Figure 9b shows the test error obtained as a function of $p$. We notice that the magnitude of errors for small values of $p$ has reduced by a lot compared to Figure 9a (for $p = 0.1$ it fell from 2.7% to 1.7%). Values of $p$ that are close to 0.6 seem to perform best for this choice of $pn$ but our usual default value of 0.5 is close to optimal.

Figure 9: Effect of changing dropout rates on MNIST.

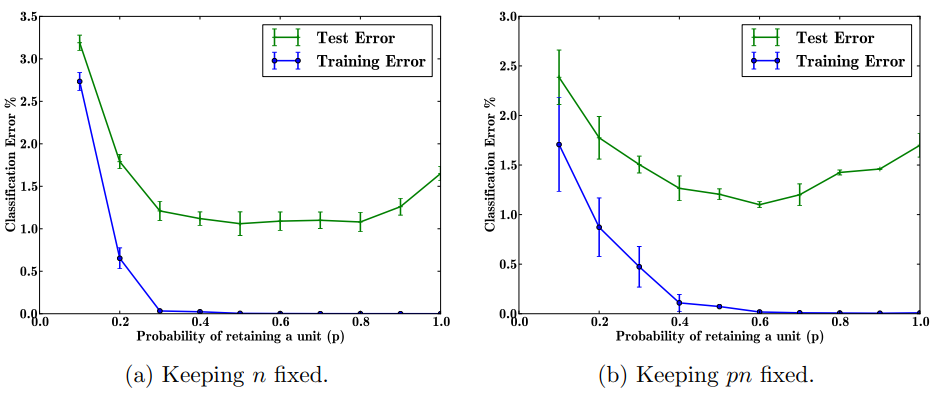
7.4 Effect of Data Set Size

One test of a good regularizer is that it should make it possible to get good generalization error from models with a large number of parameters trained on small data sets. This section explores the effect of changing the data set size when dropout is used with feedforward networks. Huge neural networks trained in the standard way overfit massively on small data sets. To see if dropout can help, we run classification experiments on MNIST and vary the amount of data given to the network.

The results of these experiments are shown in Figure 10. The network was given data sets of size 100, 500, 1K, 5K, 10K and 50K chosen randomly from the MNIST training set. The same network architecture (784-1024-1024-2048-10) was used for all data sets. Dropout with p = 0.5 was performed at all the hidden layers and p = 0.8 at the input layer. It can be observed that for extremely small data sets (100, 500) dropout does not give any improvements. The model has enough parameters that it can overfit on the training data, even with all the noise coming from dropout. As the size of the data set is increased, the gain from doing dropout increases up to a point and then declines. This suggests that for any given architecture and dropout rate, there is a "sweet spot" corresponding to some amount of data that is large enough to not be memorized in spite of the noise but not so large that overfitting is not a problem anyways.

Figure 10: Effect of varying data set size.

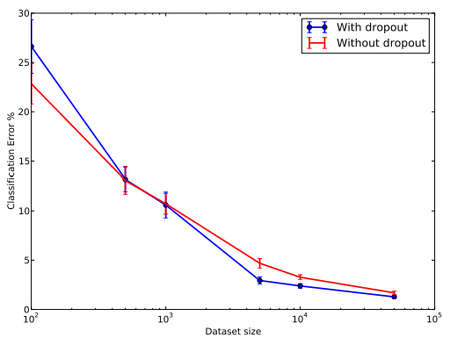
7.5 Monte-Carlo Model Averaging vs. Weight Scaling

The efficient test time procedure that we propose is to do an approximate model combination by scaling down the weights of the trained neural network. An expensive but more correct way of averaging the models is to sample $k$ neural nets using dropout for each test case and average their predictions. As $k \to \infty$, this Monte-Carlo model average gets close to the true model average. It is interesting to see empirically how many samples $k$ are needed to match the performance of the approximate averaging method. By computing the error for different values of $k$ we can see how quickly the error rate of the finite-sample average approaches the error rate of the true model average.

We again use the MNIST data set and do classification by averaging the predictions of $k$ randomly sampled neural networks. Figure 11 shows the test error rate obtained for different values of $k$. This is compared with the error obtained using the weight scaling method (shown as a horizontal line). It can be seen that around $k = 50$, the Monte-Carlo method becomes as good as the approximate method. Thereafter, the Monte-Carlo method is slightly better than the approximate method but well within one standard deviation of it. This suggests that the weight scaling method is a fairly good approximation of the true model average.

Figure 11: Monte-Carlo model averaging vs. weight scaling.

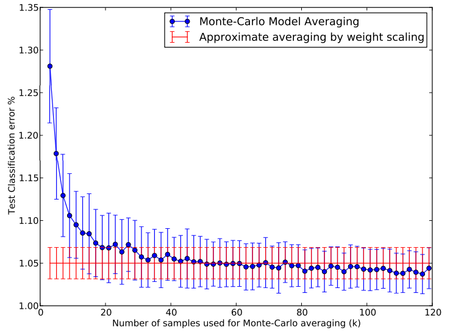
8. Dropout Restricted Boltzmann Machines

Besides feed-forward neural networks, dropout can also be applied to Restricted Boltzmann Machines (RBM). In this section, we formally describe this model and show some results to illustrate its key properties.

8.1 Model Description

Consider an RBM with visible units $\mathbf{v} \in \{0,1\}^D$ and hidden units $\mathbf{h} \in \{0,1\}^F$ . It defines the following probability distribution

$P(\mathbf{h}, \mathbf{v} ; \theta)=\dfrac{1}{\mathcal{Z}(\theta)} \exp \left(\mathbf{v}^{\top} W \mathbf{h}+\mathbf{a}^{\top} \mathbf{h}+\mathbf{b}^{\top} \mathbf{v}\right)$

Where $\theta = \{W, \mathbf{a}, \mathbf{b}\}$ represents the model parameters and $\mathcal{Z}$ is the partition function.

 Dropout RBMs are RBMs augmented with a vector of binary random variables $\mathbf{r} \in \{0, 1\}^F$ . Each random variable $r_j$ takes the value $1$ with probability $p$, independent of others. If $r_j$ takes the value 1, the hidden unit $h_j$ is retained, otherwise it is dropped from the model. The joint distribution defined by a Dropout RBM can be expressed as

$\begin{aligned} P(\mathbf{r}, \mathbf{h}, \mathbf{v} ; p, \theta) &=P(\mathbf{r} ; p) P(\mathbf{h}, \mathbf{v} \mid \mathbf{r} ; \theta) \\ P(\mathbf{r} ; p) &=\prod_{j=1}^{F} p^{r_{j}}(1-p)^{1-r_{j}} \\ P(\mathbf{h}, \mathbf{v} \mid \mathbf{r} ; \theta) &=\dfrac{1}{\mathcal{Z}^{\prime}(\theta, \mathbf{r})} \exp \left(\mathbf{v}^{\top} W \mathbf{h}+\mathbf{a}^{\top} \mathbf{h}+\mathbf{b}^{\top} \mathbf{v}\right) \prod_{j=1}^{F} g\left(h_{j}, r_{j}\right) \\ g\left(h_{j}, r_{j}\right) &=\mathbb{1}\left(r_{j}=1\right)+\mathbb{1}\left(r_{j}=0\right) \mathbb{1}\left(h_{j}=0\right) \end{aligned}$

$\mathcal{Z}^{\prime}(\theta, \mathbf{r})$ is the normalization constant. $g(h_j, r_j)$ imposes the constraint that if $r_j = 0$, $h_j$ must be 0. The distribution over $\mathbf{h}$, conditioned on $\mathbf{v}$ and $\mathbf{r}$ is factorial

$\begin{aligned} P(\mathbf{h} \mid \mathbf{r}, \mathbf{v}) &=\prod_{j=1}^{F} P\left(h_{j} \mid r_{j}, \mathbf{v}\right) \\ P\left(h_{j}=1 \mid r_{j}, \mathbf{v}\right) &=\mathbb{1}\left(r_{j}=1\right) \sigma\left(b_{j}+\sum_{i} W_{i j} v_{i}\right) \end{aligned}$

The distribution over $\mathbf{v}$ conditioned on $\mathbf{h}$ is same as that of an RBM

$\begin{aligned} P(\mathbf{v} \mid \mathbf{h}) &=\prod_{i=1}^{D} P\left(v_{i} \mid \mathbf{h}\right) \\ P\left(v_{i}=1 \mid \mathbf{h}\right) &=\sigma\left(a_{i}+\sum_{j} W_{i j} h_{j}\right) \end{aligned}$

Conditioned on $\mathbf{r}$, the distribution over $\{\mathbf{v}, \mathbf{h}\}$ is same as the distribution that an RBM would impose, except that the units for which $r_j = 0$ are dropped from $\mathbf{h}$. Therefore, the Dropout RBM model can be seen as a mixture of exponentially many RBMs with shared weights each using a different subset of $\mathbf{h}$.

8.2 Learning Dropout RBMs

Learning algorithms developed for RBMs such as Contrastive Divergence (Hinton et al., 2006) can be directly applied for learning Dropout RBMs. The only difference is that $\mathbf{r}$ is first sampled and only the hidden units that are retained are used for training. Similar to dropout neural networks, a different $\mathbf{r}$ is sampled for each training case in every minibatch. In our experiments, we use CD-1 for training dropout RBMs.

8.3 Effect on Features

Dropout in feed-forward networks improved the quality of features by reducing co-adaptations. This section explores whether this effect transfers to Dropout RBMs as well. Figure 12a shows features learned by a binary RBM with 256 hidden units. Figure 12b shows features learned by a dropout RBM with the same number of hidden units. Features learned by the dropout RBM appear qualitatively different in the sense that they seem to capture features that are coarser compared to the sharply defined stroke-like features in the standard RBM. There seem to be very few dead units in the dropout RBM relative to the standard RBM.

Figure 12: Features learned on MNIST by 256 hidden unit RBMs. The features are ordered by L2 norm.

8.4 Effect on Sparsity

Next, we investigate the effect of dropout RBM training on sparsity of the hidden unit activations. Figure 13a shows the histograms of hidden unit activations and their means on a test mini-batch after training an RBM. Figure 13b shows the same for dropout RBMs. The histograms clearly indicate that the dropout RBMs learn much sparser representations than standard RBMs even when no additional sparsity inducing regularizer is present.

Figure 13: Effect of dropout on sparsity. Left: The activation histogram shows that a large number of units have activations away from zero. Right: A large number of units have activations close to zero and very few units have high activation.

9. Marginalizing Dropout

Dropout can be seen as a way of adding noise to the states of hidden units in a neural network. In this section, we explore the class of models that arise as a result of marginalizing this noise. These models can be seen as deterministic versions of dropout. In contrast to standard ("Monte-Carlo") dropout, these models do not need random bits and it is possible to get gradients for the marginalized loss functions. In this section, we briefly explore these models.

 Deterministic algorithms have been proposed that try to learn models that are robust to feature deletion at test time (Globerson and Roweis, 2006). Marginalization in the context of denoising autoencoders has been explored previously (Chen et al., 2012). The marginalization of dropout noise in the context of linear regression was discussed in Srivastava (2013). Wang and Manning (2013) further explored the idea of marginalizing dropout to speed-up training. van der Maaten et al. (2013) investigated different input noise distributions and the regularizers obtained by marginalizing this noise. Wager et al. (2013) describes how dropout can be seen as an adaptive regularizer.

9.1 Linear Regression

First we explore a very simple case of applying dropout to the classical problem of linear regression. Let $X \in \R^{N\times D}$ be a data matrix of $N$ data points. $\mathbf{y}\in \R^N$ be a vector of targets. Linear regression tries to find a $\mathbf{w}\in \R^D$ that minimizes

$|| \mathbf{y}-X \mathbf{w} \|^{2}e$

When the input $X$ is dropped out such that any input dimension is retained with probability $p$, the input can be expressed as $R\star X$ where $R \in \{0, 1\}^{N\times D}$ is a random matrix with $R_{ij} \sim Bernoulli(p)$ and $\star$ denotes an element-wise product. Marginalizing the noise, the objective function becomes

$\underset{\mathbf{w}}{\operatorname{minimize}} \quad \mathbb{E}_{R \sim \text {Bernoulli}(\mathrm{p})}\left[\|\mathbf{y}-(R * X) \mathbf{w}\|^{2}\right]$

This reduces to

$\underset{\mathbf{w}}{\operatorname{minimize}}\|\mathbf{y}-p X \mathbf{w}\|^{2}+p(1-p)\|\Gamma \mathbf{w}\|^{2}$

where $\Gamma=\left(\operatorname{diag}\left(X^{\top} X\right)\right)^{1 / 2}$. Therefore, dropout with linear regression is equivalent, in expectation, to ridge regression with a particular form for $\Gamma$. This form of essentially scales the weight cost for weight $w_i$ by the standard deviation of the ith dimension of the data. If a particular data dimension varies a lot, the regularizer tries to squeeze its weight more.

Another interesting way to look at this objective is to absorb the factor of $p$ into $\mathbf{w}$. This leads to the following form

$$\underset{\mathbf{w}}{\operatorname{minimize}} \quad\|\mathbf{y}-X \tilde{\mathbf{w}}\|^{2}+\frac{1-p}{p}\|\Gamma \tilde{\mathbf{w}}\|^{2}$$

where $\mathbf{\tilde{w}} = p\mathbf{w}$. This makes the dependence of the regularization constant on $p$ explicit. For $p$ close to $1$, all the inputs are retained and the regularization constant is small. As more dropout is done (by decreasing $p$), the regularization constant grows larger.

9.2 Logistic Regression and Deep Networks

For logistic regression and deep neural nets, it is hard to obtain a closed form marginalized model. However, Wang and Manning (2013) showed that in the context of dropout applied to logistic regression, the corresponding marginalized model can be trained approximately. Under reasonable assumptions, the distributions over the inputs to the logistic unit and over the gradients of the marginalized model are Gaussian. Their means and variances can be computed efficiently. This approximate marginalization outperforms Monte-Carlo dropout in terms of training time and generalization performance.

However, the assumptions involved in this technique become successively weaker as more layers are added. Therefore, the results are not directly applicable to deep networks.

10. Multiplicative Gaussian Noise

Dropout involves multiplying hidden activations by Bernoulli distributed random variables which take the value $1$ with probability $p$ and $0$ otherwise. This idea can be generalized by multiplying the activations with random variables drawn from other distributions. We recently discovered that multiplying by a random variable drawn from $\mathcal{N} (1, 1)$ works just as well, or perhaps better than using Bernoulli noise. This new form of dropout amounts to adding a Gaussian distributed random variable with zero mean and standard deviation equal to the activation of the unit. That is, each hidden activation $h_i$ is perturbed to $h_i + h_ir$ where $r \sim \mathcal{N} (0, 1)$, or equivalently $h_ir'$ where $r' \sim \mathcal{N}(1, 1)$. We can generalize this to $r' \sim \N (1, \sigma^2)$ where $\sigma$ becomes an additional hyperparameter to tune, just like $p$ was in the standard (Bernoulli) dropout. The expected value of the activations remains unchanged, therefore no weight scaling is required at test time.

In this paper, we described dropout as a method where we retain units with probability $p$ at training time and scale down the weights by multiplying them by a factor of $p$ at test time. Another way to achieve the same effect is to scale up the retained activations by multiplying by $1/p$ at training time and not modifying the weights at test time. These methods are equivalent with appropriate scaling of the learning rate and weight initializations at each layer.

Therefore, dropout can be seen as multiplying $h_i$ by a Bernoulli random variable $r_b$ that takes the value $1/p$ with probability $p$ and $0$ otherwise. $E [r_b] = 1$ and $Var[r_b]= (1-p)/p$. For the Gaussian multiplicative noise, if we set $\sigma^2 = (1-p)/p$, we end up multiplying $h_i$ by a random variable $r_g$, where $E[r_g] = 1$ and $Var[r_g] = (1-p)/p$. Therefore, both forms of dropout can be set up so that the random variable being multiplied by has the same mean and variance. However, given these first and second order moments, $r_g$ has the highest entropy and $r_b$ has the lowest. Both these extremes work well, although preliminary experimental results shown in Table 10 suggest that the high entropy case might work slightly better. For each layer, the value of $\sigma$ in the Gaussian model was set to be $\sqrt{\frac{1-p}{p}}$ using the $p$ from the corresponding layer in the Bernoulli model.

Table 10: Comparison of classification error % with Bernoulli and Gaussian dropout. For MNIST, the Bernoulli model uses $p = 0.5$ for the hidden units and $p = 0.8$ for the input units. For CIFAR-10, we use $p = (0.9, 0.75, 0.75, 0.5, 0.5, 0.5)$ going from the input layer to the top. The value of $\sigma$ for the Gaussian dropout models was set to be $\sqrt{\frac{1-p}{p}}$. Results were averaged over 10 different random seeds.

Data Set	Architecture	Bernoulli dropout	Gaussian dropout
MNIST	2 layers, 1024 units each	$1.08\pm 0.04$	$0.95 \pm 0.04$
CIFAR-10	3 conv + 2 fully connected layers	$12.6 \pm 0.1$	$12.5 \pm 0.1$

=== 11. Conclusion === Dropout is a technique for improving neural networks by reducing overfitting. Standard backpropagation learning builds up brittle co-adaptations that work for the training data but do not generalize to unseen data. Random dropout breaks up these co-adaptations by making the presence of any particular hidden unit unreliable. This technique was found to improve the performance of neural nets in a wide variety of application domains including object classification, digit recognition, speech recognition, document classification and analysis of computational biology data. This suggests that dropout is a general technique and is not specific to any domain. Methods that use dropout achieve state-of-the-art results on SVHN, ImageNet, CIFAR-100 and MNIST. Dropout considerably improved the performance of standard neural nets on other data sets as well.

This idea can be extended to Restricted Boltzmann Machines and other graphical models. The central idea of dropout is to take a large model that overfits easily and repeatedly sample and train smaller sub-models from it. RBMs easily fit into this framework. We developed Dropout RBMs and empirically showed that they have certain desirable properties. One of the drawbacks of dropout is that it increases training time. A dropout network typically takes 2-3 times longer to train than a standard neural network of the same architecture. A major cause of this increase is that the parameter updates are very noisy. Each training case effectively tries to train a different random architecture. Therefore, the gradients that are being [[computed are not gradients of the final architecture that will be used at test time. Therefore, it is not surprising that training takes a long time. However, it is likely that this stochasticity prevents overfitting. This creates a trade-off between overfitting and training time. With more training time, one can use high dropout and suffer less overfitting. However, one way to obtain some of the benefits of dropout without stochasticity is to marginalize the noise to obtain a regularizer that does the same thing as the dropout procedure, in expectation. We showed that for linear regression this regularizer is a modiffed form of L2 regularization. For more complicated models, it is not obvious how to obtain an equivalent regularizer. Speeding up dropout is an interesting direction for future work.

Appendix A. A Practical Guide for Training Dropout Networks

Neural networks are infamous for requiring extensive hyperparameter tuning. Dropout networks are no exception. In this section, we describe heuristics that might be useful for applying dropout.

A.1 Network Size

It is to be expected that dropping units will reduce the capacity of a neural network. If $n$ is the number of hidden units in any layer and $p$ is the probability of retaining a unit, then instead of $n$ hidden units, only $pn$ units will be present after dropout, in expectation. Moreover, this set of $pn$ units will be different each time and the units are not allowed to build co-adaptations freely. Therefore, if an $n$-sized layer is optimal for a standard neural net on any given task, a good dropout net should have at least $n/p$ units. We found this to be a useful heuristic for setting the number of hidden units in both convolutional and fully connected networks.

A.2 Learning Rate and Momentum

Dropout introduces a significant amount of noise in the gradients compared to standard stochastic gradient descent. Therefore, a lot of gradients tend to cancel each other. In order to make up for this, a dropout net should typically use 10-100 times the learning rate that was optimal for a standard neural net. Another way to reduce the effect the noise is to use a high momentum. While momentum values of 0.9 are common for standard nets, with dropout we found that values around 0.95 to 0.99 work quite a lot better. Using high learning rate and/or momentum significantly speed up learning.

A.3 Max-norm Regularization

Though large momentum and learning rate speed up learning, they sometimes cause the network weights to grow very large. To prevent this, we can use max-norm regularization. This constrains the norm of the vector of incoming weights at each hidden unit to be bound by a constant $c$. Typical values of $c$ range from $3$ to $4$.

A.4 Dropout Rate

Dropout introduces an extra hyperparameter - the probability of retaining a unit $p$. This hyperparameter controls the intensity of dropout. $p = 1$, implies no dropout and low values of $p$ mean more dropout. Typical values of $p$ for hidden units are in the range $0.5$ to $0.8$. For input layers, the choice depends on the kind of input. For real-valued inputs (image patches or speech frames), a typical value is $0.8$. For hidden layers, the choice of $p$ is coupled with the choice of number of hidden units $n$. Smaller $p$ requires big $n$ which slows down the training and leads to underfitting. Large $p$ may not produce enough dropout to prevent overfitting.

Appendix B. Detailed Description of Experiments and Data Sets

This section describes the network architectures and training details for the experimental results reported in this paper. The code for reproducing these results can be obtained from http://www.cs.toronto.edu/~nitish/dropout. The implementation is GPU-based. We used the excellent CUDA libraries- cudamat (Mnih, 2009) and cuda-convnet (Krizhevsky et al., 2012) to implement our networks.

B.1 MNIST

The MNIST data set consists of $60,000$ training and $10,000$ test examples each representing a $28\times 28$ digit image. We held out $10,000$ random training images for validation. Hyperparameters were tuned on the validation set such that the best validation error was produced after 1 million weight updates. The validation set was then combined with the training set and training was done for 1 million weight updates. This net was used to evaluate the performance on the test set. This way of using the validation set was chosen because we found that it was easy to set up hyperparameters so that early stopping was not required at all. Therefore, once the hyperparameters were fixed, it made sense to combine the validation and training sets and train for a very long time.

The architectures shown in Figure 4 include all combinations of 2, 3, and 4 layer networks with 1024 and 2048 units in each layer. Thus, there are six architectures in all. For all the architectures (including the ones reported in Table 2), we used $p = 0.5$ in all hidden layers and $p = 0.8$ in the input layer. A final momentum of $0.95$ and weight constraints with $c = 2$ was used in all the layers.

To test the limits of dropout's regularization power, we also experimented with 2 and 3 layer nets having $4096$ and $8192$ units. 2 layer nets gave improvements as shown in Table 2. However, the three layer nets performed slightly worse than 2 layer ones with the same level of dropout. When we increased dropout, performance improved but not enough to outperform the 2 layer nets.

B.2 SVHN

The SVHN data set consists of approximately 600,000 training images and 26,000 test images. The training set consists of two parts - A standard labeled training set and another set of labeled examples that are easy. A validation set was constructed by taking examples from both the parts. Two-thirds of it were taken from the standard set (400 per class) and one-third from the extra set (200 per class), a total of 6000 samples. This same process is used by Sermanet et al. (2012). The inputs were RGB pixels normalized to have zero mean and unit variance. Other preprocessing techniques such as global or local contrast normalization or ZCA whitening did not give any noticeable improvements.

The best architecture that we found uses three convolutional layers each followed by a max-pooling layer. The convolutional layers have 96, 128 and 256 filters respectively. Each convolutional layer has a $5 \times 5$ receptive field applied with a stride of 1 pixel. Each max pooling layer pools $3 \times 3$ regions at strides of 2 pixels. The convolutional layers are followed by two fully connected hidden layers having 2048 units each. All units use the rectiffed linear activation function. Dropout was applied to all the layers of the network with the probability of retaining the unit being $p = (0.9, 0.75, 0.75, 0.5, 0.5, 0.5)$ for the different layers of the network (going from input to convolutional layers to fully connected layers). In addition, the max-norm constraint with $c = 4$ was used for all the weights. A momentum of 0.95 was used in all the layers. These hyperparameters were tuned using a validation set. Since the training set was quite large, we did not combine the validation set with the training set for final training. We reported test error of the model that had smallest validation error.

B.3 CIFAR-10 and CIFAR-100

The CIFAR-10 and CIFAR-100 data sets consists of 50,000 training and 10,000 test images each. They have 10 and 100 image categories respectively. These are $32 \times 32$ color images. We used 5,000 of the training images for validation. We followed the procedure similar to MNIST, where we found the best hyperparameters using the validation set and then combined it with the training set. The images were preprocessed by doing global contrast normalization in each color channel followed by ZCA whitening. Global contrast normalization means that for image and each color channel in that image, we compute the mean of the pixel intensities and subtract it from the channel. ZCA whitening means that we mean center the data, rotate it onto its principle components, normalize each component and then rotate it back. The network architecture and dropout rates are same as that for SVHN, except the learning rate s for the input layer which had to be set to smaller values.

B.4 TIMIT

The open source Kaldi toolkit (Povey et al., 2011) was used to preprocess the data into log-filter banks. A monophone system was trained to do a forced alignment and to get labels for speech frames. Dropout neural networks were trained on windows of 21 consecutive frames to predict the label of the central frame. No speaker dependent operations were performed. The inputs were mean centered and normalized to have unit variance. We used probability of retention $p = 0.8$ in the input layers and 0.5 in the hidden layers. Max-norm constraint with $c = 4$ was used in all the layers. A momentum of 0.95 with a high learning rate of 0.1 was used. The learning rate was decayed as $\epsilon_0 (1 + t/T)^{-1}$. For DBN pretraining, we trained RBMs using CD-1. The variance of each input unit for the Gaussian RBM was fixed to 1. For finetuning the DBN with dropout, we found that in order to get the best results it was important to use a smaller learning rate (about 0.01). Adding max-norm constraints did not give any improvements.

B.5 Reuters

The Reuters RCV1 corpus contains more than 800,000 documents categorized into 103 classes. These classes are arranged in a tree hierarchy. We created a subset of this data set consisting of 402,738 articles and a vocabulary of 2000 words comprising of 50 categories in which each document belongs to exactly one class. The data was split into equal sized training and test sets. We tried many network architectures and found that dropout gave improvements in classification accuracy over all of them. However, the improvement was not as significant as that for the image and speech data sets. This might be explained by the fact that this data set is quite big (more than 200,000 training examples) and overfitting is not a very serious problem.

B.6 Alternative Splicing

The alternative splicing data set consists of data for 3665 cassette exons, 1014 RNA features and 4 tissue types derived from 27 mouse tissues. For each input, the target consists of 4 softmax units (one for tissue type). Each softmax unit has 3 states (inc, exc, nc) which are of the biological importance. For each softmax unit, the aim is to predict a distribution over these 3 states that matches the observed distribution from wet lab experiments as closely as possible. The evaluation metric is Code Quality which is defined as

$\sum_{i=1}^{\text {|data points } \mid} \sum_{t \in \text { tissue types } s \in\{\text { inc }, \text { exc }, \text { nc }\}} p_{i, t}^{s} \log \left(\frac{q_{t}^{s}\left(r_{i}\right)}{\bar{p}^{s}}\right)$

where, $p_{i, t}^{s}$ is the target probability for state $s$ and tissue type $t$ in input $i; q^s_t(r_i)$ is the predicted probability for state $s$ in tissue type $t$ for input $r_i$ and $\overline{p}^s$ is the average of $p_{i, t}^{s}$ over $i$ and $t$.

A two layer dropout network with 1024 units in each layer was trained on this data set. A value of $p = 0.5$ was used for the hidden layer and $p = 0.7$ for the input layer. Max-norm regularization with high decaying learning rate $s$ was used. Results were averaged across the same 5 folds used by Xiong et al. (2011).

References

• 1. M. Chen, Z. Xu, K. Weinberger, and F. Sha. Marginalized Denoising Autoencoders for Domain Adaptation. In Proceedings of the 29th International Conference on Machine Learning, Pages 767-774. ACM, 2012.
• 2. G. E. Dahl, M. Ranzato, A. Mohamed, and G. E. Hinton. Phone Recognition with the Mean-covariance Restricted Boltzmann Machine. In Advances in Neural Information Processing Systems 23, Pages 469-477, 2010.
• 3. Ofer Dekel, Ohad Shamir, Lin Xiao, Learning to Classify with Missing and Corrupted Features, Machine Learning, v.81 n.2, p.149-178, November 2010
• 4. Amir Globerson, Sam Roweis, Nightmare at Test Time: Robust Learning by Feature Deletion, Proceedings of the 23rd International Conference on Machine Learning, p.353-360, June 25-29, 2006, Pittsburgh, Pennsylvania, USA
• 5. I. J. Goodfellow, D. Warde-Farley, M. Mirza, A. Courville, and Y. Bengio. Maxout Networks. In Proceedings of the 30th International Conference on Machine Learning, Pages 1319- 1327. ACM, 2013.
• 6. G. Hinton and R. Salakhutdinov. Reducing the Dimensionality of Data with Neural Networks. Science, 313(5786):504-507, 2006.
• 7. Geoffrey E. Hinton, Simon Osindero, Yee-Whye Teh, A Fast Learning Algorithm for Deep Belief Nets, Neural Computation, v.18 n.7, p.1527-1554, July 2006
• 8. K. Jarrett, K. Kavukcuoglu, M. Ranzato, and Y. LeCun. What is the Best Multi-stage Architecture for Object Recognition? In Proceedings of the International Conference on Computer Vision (ICCV'09). IEEE, 2009.
• 9. A. Krizhevsky. Learning Multiple Layers of Features from Tiny Images. Technical Report, University of Toronto, 2009.
• 10. A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems 25, Pages 1106-1114, 2012.
• 11. Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, L. D. Jackel, Backpropagation Applied to Handwritten Zip Code Recognition, Neural Computation, v.1 n.4, p.541-551, Winter 1989
• 12. Y. Lin, F. Lv, S. Zhu, M. Yang, T. Cour, K. Yu, L. Cao, Z. Li, M.-H. Tsai, X. Zhou, T. Huang, and T. Zhang. Imagenet Classification: Fast Descriptor Coding and Large-scale Svm Training. Large Scale Visual Recognition Challenge, 2010.
• 13. A. Livnat, C. Papadimitriou, N. Pippenger, and M. W. Feldman. Sex, Mixability, and Modularity. Proceedings of the National Academy of Sciences, 107(4):1452-1457, 2010.
• 14. V. Mnih. CUDAMat: A CUDA-based Matrix Class for Python. Technical Report UTML TR 2009-004, Department of Computer Science, University of Toronto, November 2009.
• 15. A. Mohamed, G. E. Dahl, G. Hinton, Acoustic Modeling Using Deep Belief Networks, IEEE Transactions on Audio, Speech, and Language Processing, v.20 n.1, p.14-22, January 2012
• 16. Radford M. Neal, Bayesian Learning for Neural Networks, Springer-Verlag New York, Inc., Secaucus, NJ, 1996
• 17. Y. Netzer, T. Wang, A. Coates, A. Bissacco, B. Wu, and A. Y. Ng. Reading Digits in Natural Images with Unsupervised Feature Learning. In NIPS Workshop on Deep Learning and Unsupervised Feature Learning 2011, 2011.
• 18. Steven J. Nowlan, Geoffrey E. Hinton, Simplifying Neural Networks by Soft Weight-sharing, Neural Computation, v.4 n.4, p.473-493, July 1992
• 19. D. Povey, A. Ghoshal, G. Boulianne, L. Burget, O. Glembek, N. Goel, M. Hannemann, P. Motlicek, Y. Qian, P. Schwarz, J. Silovsky, G. Stemmer, and K. Vesely. The Kaldi Speech Recognition Toolkit. In IEEE 2011 Workshop on Automatic Speech Recognition and Understanding. IEEE Signal Processing Society, 2011.
• 20. R. Salakhutdinov and G. Hinton. Deep Boltzmann Machines. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Volume 5, Pages 448-455, 2009.
• 21. Ruslan Salakhutdinov, Andriy Mnih, Bayesian Probabilistic Matrix Factorization Using Markov Chain Monte Carlo, Proceedings of the 25th International Conference on Machine Learning, p.880-887, July 05-09, 2008, Helsinki, Finland
• 22. J. Sanchez, F. Perronnin, High-dimensional Signature Compression for Large-scale Image Classification, Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition, p.1665-1672, June 20-25, 2011
• 23. P. Sermanet, S. Chintala, and Y. LeCun. Convolutional Neural Networks Applied to House Numbers Digit Classification. In International Conference on Pattern Recognition (ICPR 2012), 2012.
• 24. Patrice Y. Simard, Dave Steinkraus, John C. Platt, Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis, Proceedings of the Seventh International Conference on Document Analysis and Recognition, p.958, August 03-06, 2003
• 25. J. Snoek, H. Larochelle, and R. Adams. Practical Bayesian Optimization of Machine Learning Algorithms. In Advances in Neural Information Processing Systems 25, Pages 2960-2968, 2012.
• 26. Nathan Srebro, Adi Shraibman, Rank, Trace-norm and Max-norm, Proceedings of the 18th Annual Conference on Learning Theory, June 27-30, 2005, Bertinoro, Italy
• 27. N. Srivastava. Improving Neural Networks with Dropout. Master's Thesis, University of Toronto, January 2013.
• 28. R. Tibshirani. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society. Series B. Methodological, 58(1):267-288, 1996.
• 29. A. N. Tikhonov. On the Stability of Inverse Problems. Doklady Akademii Nauk SSSR, 39(5): 195-198, 1943.
• 30. L. Van Der Maaten, M. Chen, S. Tyree, and K. Q. Weinberger. Learning with Marginalized Corrupted Features. In Proceedings of the 30th International Conference on Machine Learning, Pages 410-418. ACM, 2013.
• 31. Pascal Vincent, Hugo Larochelle, Yoshua Bengio, Pierre-Antoine Manzagol, Extracting and Composing Robust Features with Denoising Autoencoders, Proceedings of the 25th International Conference on Machine Learning, p.1096-1103, July 05-09, 2008, Helsinki, Finland
• 32. P. Vincent, H. Larochelle, I. Lajoie, Y. Bengio, and P.-A. Manzagol. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. In Proceedings of the 27th International Conference on Machine Learning, Pages 3371-3408. ACM, 2010.
• 33. S. Wager, S. Wang, and P. Liang. Dropout Training As Adaptive Regularization. In Advances in Neural Information Processing Systems 26, Pages 351-359, 2013.
• 34. S. Wang and C. D. Manning. Fast Dropout Training. In Proceedings of the 30th International Conference on Machine Learning, Pages 118-126. ACM, 2013.
• 35. Hui Yuan Xiong, Yoseph Barash, Brendan J. Frey, Bayesian Prediction of Tissue-regulated Splicing Using RNA Sequence and Cellular Context, Bioinformatics, v.27 n.18, p.2554-2562, September 2011
• 36. M. D. Zeiler and R. Fergus. Stochastic Pooling for Regularization of Deep Convolutional Neural Networks. CoRR, Abs/1301.3557, 2013.

BibTeX

@article{2014_DropoutASimpleWaytoPreventNeura,
  author    = {Nitish Srivastava and
               Geoffrey E. Hinton and
               Alex Krizhevsky and
 [[Ilya Sutskever]] and
               Ruslan Salakhutdinov},
  title     = {Dropout: a simple way to prevent neural networks from overfitting},
  journal   = {J. Mach. Learn. Res.},
  volume    = {15},
  number    = {1},
  pages     = {1929--1958},
  year      = {2014},
  url       = {http://dl.acm.org/citation.cfm?id=2670313},
}

---

	Author	volume	Date Value	title	type	journal	titleUrl	doi	note	year
2014 DropoutASimpleWaytoPreventNeura	Geoffrey E. Hinton Ilya Sutskever Ruslan Salakhutdinov Nitish Srivastava Alex Krizhevsky			Dropout: A Simple Way to Prevent Neural Networks from Overfitting						2014