2016 AReviewofRelationalMachineLearn

From GM-RKB
Jump to navigation Jump to search

Subject Headings: Relational Machine Learning Algorithm, SPO Triple, Google Knowledge Vault.

Notes

Cited By

Quotes

Abstract

Relational machine learning studies methods for the statistical analysis of relational, or graph-structured data. In this paper, we provide a review of how such statistical models can be “trained” on large knowledge graphs, and then used to predict new facts about the world (which is equivalent to predicting new edges in the graph). In particular, we discuss two fundamentally different kinds of statistical relational models, both of which can scale to massive data sets. The first is based on latent feature models such as tensor factorization and multi-way neural networks. The second is based on mining observable patterns in the graph. We also show how to combine these latent and observable models to get improved modeling power at decreased computational cost. Finally, we discuss how such statistical models of graphs can be combined with text-based information extraction methods for automatically constructing knowledge graphs from the Web. To this end, we also discuss Google's knowledge vault project as an example of such combination.

I. INTRODUCTION

‘‘I am convinced that the crux of the problem of learning is recognizing relationships and being able to use them’’

Christopher Strachey in a letter to Alan Turing, 1954.

 Traditional machine learning algorithms take as input a feature vector, which represents an object in terms of numeric or categorical attributes. The main learning task is to learn a mapping from this feature vector to an output prediction of some form. This could be class labels, a regression score, or an unsupervised cluster id or latent vector (embedding). In statistical relational learning (SRL), the representation of an object can contain its relationships to other objects. Thus the data is in the form of a graph, consisting of nodes (entities) and labeled edges (relationships between entities). The main goals of SRL include prediction of missing edges, prediction of properties of nodes, and clustering nodes based on their connectivity patterns. These tasks arise in many settings such as analysis of social networks and biological pathways. For further information on SRL, see [1]–[3].

 In this paper, we review a variety of techniques from the SRL community and explain how they can be applied to large-scale knowledge graphs (KGs), i.e., graph structured knowledge bases (KBs) that store factual information in form of relationships between entities. Recently, a large number of knowledge graphs have been created, including YAGO [4], DBpedia [5], NELL [6], Freebase [7], and the Google Knowledge Graph [8]. As we discuss in Section II, these graphs contain millions of nodes and billions of edges. This causes us to focus on scalable SRL techniques, which take time that is (at most) linear in the size of the graph.

We can apply SRL methods to existing KGs to learn a model that can predict new facts (edges) given existing facts. We can then combine this approach with information extraction methods that extract ‘‘noisy’’ facts from the Web (see, e.g., [9] and [10]). For example, suppose an information extraction method returns a fact claiming that Barack Obama was born in Kenya, and suppose (for illustration purposes) that the true place of birth of Obama was not already stored in the knowledge graph. An SRL model can use related facts about Obama (such as his profession being U.S. President) to infer that this new fact is unlikely to be true and should be discarded. This provides us a way to ‘‘grow’’ a KG automatically, as we explain in more detail in Section IX.

The remainder of this paper is structured as follows. In Section II, we introduce knowledge graphs and some of their properties. Section III discusses SRL and how it can be applied to knowledge graphs. There are two main classes of SRL techniques: those that capture the correlation between the nodes/ [edge]]s using latent variables, and those that capture the correlation directly using statistical models based on the observable properties of the graph. We discuss these two families in Sections IV and V, respectively. Section VI describes methods for combining these two approaches, in order to get the best of both worlds. Section VII discusses how such models can be trained on KGs. In Section VIII we discuss relational learning using Markov Random Fields. In Section IX, we describe how SRL can be used in automated knowledge base construction projects. In Section X, we discuss extensions of the presented methods, and Section XI presents our conclusions.

II. KNOWLEDGE GRAPHS

In this section, we introduce knowledge graphs, and discuss how they are represented, constructed, and used.

A. Knowledge Representation

Knowledge graphs model information in the form of entities and relationships between them. This kind of relational knowledge representation has a long history in logic and artificial intelligence [11] , for example, in semantic networks [12] and frames [13]. More recently, it has been used in the Semantic Web community with the purpose of creating a ‘‘web of data’’ that is readable by machines [14]. While this vision of the Semantic Web remains to be fully realized, parts of it have been achieved. In particular, the concept of linked data [15], [16] has gained traction, as it facilitates publishing and interlinking data on the Web in relational form using the W3C Resource Description Framework (RDF) [17], [18]. (For an introduction to knowledge representation, see, e.g., [11], [19], and [20].)

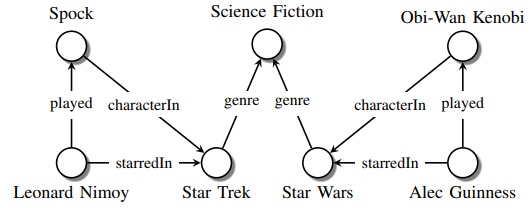
 In this paper, we will loosely follow the RDF standard and represent facts in the form of binary relationships, in particular (subject, predicate, object) (SPO) triples, where subject and object are entities and predicate is the relation between them. (We discuss how to represent higher arity relations in Section X-A.) The existence of a particular SPO triple indicates an existing fact, i.e., that the respective entities are in a relationship of the given type. For instance, the information

{|style="border: 0px; text-align:center; border-spacing: 1px; margin: 1em auto; width: 80%" |- |‘‘Leonard Nimoy was an actor who played the character Spock in the science-fiction movie Star Trek’’ |- |}

can be expressed via the following set of SPO triples:

{|class="wikitable" style="border:1px; text-align:center; solid black; border-spacing:1px; margin: 1em auto; width: 80%" |- !subject!! predicate !!object |- |(LeonardNimoy,|| profession,|| Actor) |- |(LeonardNimoy, ||starredIn, ||StarTrek) |- |(LeonardNimoy, ||played,|| Spock) |- |(Spock, ||characterIn, ||StarTrek) |- |(StarTrek,|| genre, ||ScienceFiction) |- |}

 We can combine all the SPO triple s together to form a multigraph, where nodes represent entities (all subjects and objects), and directed edges represent relationships. The direction of an edge indicates whether entities occur as subjects or objects, i.e., an edge points from the subject to the object. Different relations are represented via different types of edges (also called edge labels). This construction is called a knowledge graph (KG), or sometimes a heterogeneous information network [21].) See Fig. 1 for an example.

In addition to being a collection of facts, knowledge graphs often provide type hierarchies (Leonard Nimoy is an actor, which is a person, which is a living thing) and type constraints (e.g., a person can only marry another person, not a thing).

2016 AReviewofRelationalMachineLearn Fig1.png
Figure 1: Sample knowledge graph. Nodes represent entities, edge labels represent types of relations, edges represent existing relationships.

B. Open Versus Closed World Assumption

While existing triples always encode known true relationships (facts), there are different paradigms for the interpretation of nonexisting triples.

C. Knowledge Base Construction

Completeness, accuracy, and data quality are important parameters that determine the usefulness of knowledge bases and are influenced by the way knowledge bases are constructed. We can classify KB construction methods into four main groups:

Construction of curated knowledge bases typically leads to highly accurate results, but this technique does not scale well due to its dependence on human experts. Collaborative knowledge base construction, which was used to buildWikipedia and Freebase, scales better but still has some limitations. For instance, as mentioned previously, the place of birth attribute is missing for 71% of all people included in Freebase, even though this is a mandatory property of the schema [22]. Also, a recent study [35] found that the growth of Wikipedia has been slowing down. Consequently, automatic knowledge base construction methods have been gaining more attention.

Such methods can be grouped into two main approaches. The first approach exploits semistructured data, such as Wikipedia infoboxes, which has led to large, highly accurate knowledge graphs such as YAGO [4], [27] and DBpedia [5]. The accuracy (trustworthiness) of facts in such automatically created KGs is often still very high. For instance, the accuracy of YAGO2 has been estimated[1] to be over 95% through manual inspection of sample facts [36], and the accuracy of Freebase [7] was estimated to be 99%.[2] However, semistructured text still covers only a small fraction of the information stored on the Web, and completeness (or coverage) is another important aspect of KGs. Hence the second approach tries to ‘‘read the Web,’’ extracting facts from the natural language text of Web pages. Example projects in this category include NELL [6] and the knowledge vault [28]. In Section IX, we show how we can reduce the level of ‘‘noise’’ in such automatically extracted facts by using the knowledge from existing, high quality repositories. KGs, and more generally KBs, can also be classified based on whether they employ a fixed or open lexicon of entities and relations. In particular, we distinguish two main types of KBs.

Method Schema Examples
Curated Yes Cyc/OpenCyc [23], WordNet [24],UMLS [25]
Collaborative Yes Wikidata [26], Freebase [7]
Auto. Semi-Structured Yes YAGO [4, 27], DBPedia [5], Freebase [7]
Auto. Unstructured Yes Knowledge Vault [28], NELL [6], PATTY [29], PROSPERA [30],DeepDive/Elementary [31]
Auto. Unstructured No ReVerb [ 32], OLLIE [33], PRISMATIC [34 ]
TABLE I

KNOWLEDGE BASE CONSTRUCTION PROJECTS

  Number of
Knowledge Graph Entities Relation Types Facts
Freebase[3] 40 M 35,000 637 M
Wikidata[4] 18 M 1,632 66 M
DBpedia (en)[5] 4.6 M 1,367 538 M
YAGO2[6] 9.8 M 114 447 M
Google Knowledge Graph[7] 570 M 35,000 18,000 M
TABLE II

SIZE OF SOME SCHEMA-BASED KNOWLEDGE BASES.

D. Uses of Knowledge Graphs

Knowledge graphs provide semantically structured information that is interpretable by computers — a property that is regarded as an important ingredient to build more intelligent machines [38]. Consequently, knowledge graphs are already powering multiple "Big Data" applications in a variety of commercial and scientific domains. A prime example is the integration of Google’s Knowledge Graph, which currently stores 18 billion facts about 570 million entities, into the results of Google’s search engine [8]. The Google Knowledge Graph is used to identify and disambiguate entities in text, to enrich search results with semantically structured summaries, and to provide links to related entities in exploratory search. (Microsoft has a similar KB, called Satori, integrated with its Bing search engine [39].)

Enhancing search results with semantic information from knowledge graphs can be seen as an important step to transform text-based search engines into semantically aware question answering services. Another prominent example demonstrating the value of knowledge graphs is IBM’s question answering system Watson, which was able to beat human experts in the game of Jeopardy !. Among others, this system used YAGO, DBpedia, and Freebase as its sources of information [40]. Repositories of structured knowledge are also an indispensable component of digital assistants such as Siri, Cortana, or Google Now.

 Knowledge graphs are also used in several specialized domains. For instance, Bio2RDF [41], Neurocommons [42], and LinkedLifeData [43] are knowledge graphs that integrate multiple sources of biomedical information. These have been used for question answering and decision support in the life sciences.

E. Main Tasks in Knowledge Graph Construction and Curation

In this section, we review a number of typical KG tasks. Link prediction is concerned with predicting the existence (or probability of correctness) of (typed) edges in the graph (i.e., triples). This is important since existing knowledge graphs are often missing many facts, and some of the edges they contain are incorrect [44]. In the context of knowledge graphs, link prediction is also referred to as knowledge graph completion. For example, in Fig.1, suppose the characterIn edge]] from Obi-Wan Kenobi to Star Wars were missing; we might be able to predict this missing edge, based on the structural similarity between this part of the graph and the part involving Spock and Star Trek. It has been shown that relational models that take the relationships of entities into account can significantly outperform nonrelational machine learning methods for this task (e.g., see [45] and [46]).

 Entity resolution (also known as record linkage [47], object identification [48], instance matching [49], and deduplication [50]) is the problem of identifying which objects in relational data refer to the same underlying entities. See Fig. 2 for a small example. In a relational setting, the decisions about which objects are assumed to be identical can propagate through the graph, so that matching decisions are made collectively for all objects in a domain rather than independently for each object pair (see, for example, [51] – [53]). In schema-based automated knowledge base construction, entity resolution can be used to match the extracted surface names to entities stored in the knowledge graph.

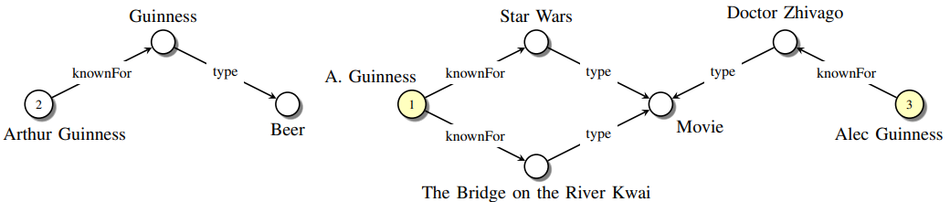
2016 AReviewofRelationalMachineLearn Fig2.png
Figure 2. Example of entity resolution in a toy knowledge graph. In this example, nodes 1 and 3 refer to the identical entity, the actor Alec Guinness. Node 2, on the other hand, refers to Arthur Guinness, the founder of the Guinness brewery. The surface name of node 2 (‘"A. Guinness") alone would not be sufficient to perform a correct matching as it could refer to both Alec Guinness and Arthur Guinness. However, since links in the graph reveal the occupations of the persons, a relational approach can perform the correct matching.

 Link-based clustering extends feature-based clustering to a relational learning setting and groups entities in relational data based on their similarity. However, in link-based clustering, entities are not only grouped by the similarity of their features but also by the similarity of their links. As in entity resolution, the similarity of entities can propagate through the knowledge graph, such that relational modeling can add important information for this task. In social network analysis, link-based clustering is also known as community detection [54].

III. STATISTICAL RELATIONAL LEARNING FOR KNOWLEDGE GRAPHS

Statistical Relational Learning is concerned with the creation of statistical models for relational data. In the following sections we discuss how statistical relational learning can be applied to knowledge graphs. We will assume that all the entities and (types of) relations in a knowledge graph are known. (We discuss extensions of this assumption in Section X-C). However, triples are assumed to be incomplete and noisy; entities and relation types may contain duplicates.

Notation: Before proceeding, let us define our mathematical notation. (Variable names will be introduced later in the appropriate sections.) We denote scalars by lower case letters, such as $a$; column vectors (of size $N$) by bold lower case letters, such as $\mathbf{a}$; matrices (of size $N_1\times N_2$) by bold upper case letters, such as $\mathbf{A}$; and tensors (of size $N_1 \times N_2 \times N_3$) by bold upper case letters with an underscore, such as $\mathbf{\underline{A}}$. We denote the $k$’ th "frontal slice" of a tensor $\mathbf{\underline{A}}$ by $\mathbf{A}_k$ (which is a matrix of size $N_1 \times N_2$), and the $(i,j,k)$’th element by $a_{ijk}$ (which is a scalar). We use $[\mathbf{a}; \mathbf{b}]$ to denote the vertical stacking of vectors $\mathbf{a}$ and $\mathbf{b}$, i.e., $[\mathbf{a}; \mathbf{b}] = \begin{pmatrix} \mathbf{a} \\ \mathbf{b} \end{pmatrix}$. We can convert a matrix $\mathbf{A}$ of size $N_1\times N_2$ into a vector a of size $N_1N_2$ by stacking all columns of $\mathbf{A}$, denoted $\mathbf{a} = vec (\mathbf{A})$. The inner (scalar) product of two vectors (both of size $N$) is defined by $\mathbf{a}^{\top} \mathbf{b} = \sum_{i-1}^N a_i b_j$. The tensor (Kronecker) product of two vectors (of size $N_1$ and $N_2$) is a vector of size $N_1N_2$ with entries

[math]\displaystyle{ \mathbf{a} \otimes \mathbf{b} = \begin{pmatrix} a_1\mathbf{b} \\ \vdots \\ a_{N_1}\mathbf{b} \end{pmatrix} }[/math].

 Matrix multiplication is denoted by $\mathbf{AB}$ as usual. We denote the $L_2$ norm of a vector by $\parallel\mathbf{a}\parallel_2= \sqrt{\sum_ia_i^2}$, and the Frobenius norm of a matrix by $\parallel \mathbf{A}\parallel_F =\sqrt{\sum_i\sum_ja^2_{ij}}$. We denote the vector of all ones by $\mathbf{1}$, and the identity matrix by $\mathbf{I}$.

A. Probabilistic Knowledge Graphs

We now introduce some mathematical background so we can more formally define statistical models for knowledge graphs.

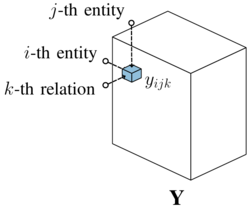
Let $\varepsilon = {e_1,\cdots,e_{N_e}}$ be the set of all entities and $\mathcal{R} = {r_1,\cdots,r_{N_r}}$ be the set of all relation types in a knowledge graph. We model each possible triple $ x_{ijk} = \left(e_i, r_k, e_j \right)$ over this set of entities and relations as a binary random variable $y_{ijk} \in \{0,1\}$ that indicates its existence. All possible triples in $\varepsilon \times \mathcal{R} \times \varepsilon$ can be grouped naturally in a third-order tensor (three-way array) $\mathbf{\underline{Y}} \in \{0,1\}^{N_e}\times N_e \times N_r$ whose entries are set such that

[math]\displaystyle{ y_{ijk}= \begin{cases} 1, & \text{if the triple} \left(e_i,r_k,e_j\right) \text{exists} \\ 0, & \text{otherwise.} \end{cases} }[/math]

We will refer to this construction as an adjacency tensor (cf. Figure 3). Each possible realization of $\mathbf{\underline{Y}}$ can be interpreted as a possible world. To derive a model for the entire knowledge graph, we are then interested in estimating the joint distribution $P\left(\mathbf{\underline{Y}}\right)$, from a subset $D \subseteq \varepsilon \times \mathcal{R} \times \varepsilon $ of observed triples. In doing so, we are estimating a probability distribution over possible worlds, which allows us to predict the probability of triples based on the state of the entire knowledge graph. While $y_{ijk} = 1$ in adjacency tensors indicates the existence of a triple, the interpretation of $y_{ijk} = 0$ depends on whether the open world, closed world, or local-closed world assumption is made. For details, see Section II-D.

Note that the size of $\mathbf{\underline{Y}}$ can be enormous for large knowledge graphs. For instance, in the case of Freebase, which currently consists of over 40 million entities and 35,000 relations, the number of possible triples $\vert \varepsilon \times \mathcal{R} \times \varepsilon\vert$ exceeds 1019 elements. Of course, type constraints reduce this number considerably.

Even amongst the syntactically valid triples, only a tiny fraction are likely to be true. For example, there are over 450,000 thousands actors and over 250,000 movies stored in Freebase. But each actor stars only in a small number of movies. Therefore, an important issue for SRL on knowledge graphs is how to deal with the large number of possible relationships while efficiently exploiting the sparsity of relationships. Ideally, a relational model for large-scale knowledge graphs should scale at most linearly with the data size, i.e., linearly in the number of entities $N_e$, linearly in the number of relations $N_r$, and linearly in the number of observed triples $\vert D\vert = N_d$.

B. Statistical Properties of Knowledge Graphs

Knowledge graphs typically adhere to some deterministic rules, such as type constraints and transitivity (e.g., if Leonard Nimoy was born in Boston, and Boston is located in the USA, then we can infer that Leonard Nimoy was born in the USA). However, KGs have typically also various “softer” statistical patterns or regularities, which are not universally true but nevertheless have useful predictive power.

One example of such statistical pattern is known as homophily, that is, the tendency of entities to be related to other entities with similar characteristics. This has been widely observed in various social networks [55, 56]. For example, US-born actors are more likely to star in US-made movies. For multi-relational data (graphs with more than one kind of link), homophily has also been referred to as autocorrelation [57].

Another statistical pattern is known as block structure. This refers to the property where entities can be divided into distinct groups (blocks), such that all the members of a group have similar relationships to members of other groups [58, 59, 60 ]. For example, we can group some actors, such as Leonard Nimoy and Alec Guinness, into a science fiction actor block, and some movies, such as Star Trek and Star Wars, into a science fiction movie block, since there is a high density of links from the scifi actor block to the scifi movie block.

 Graphs can also exhibit global and long-range statistical dependencies, i.e., dependencies that can span over chains of triples and involve different types of relations. For example, the citizenship of Leonard Nimoy (USA) depends statistically on the city where he was born (Boston), and this dependency involves a path over multiple entities (Leonard Nimoy, Boston, USA) and relations (bornIn, locatedIn, citizenOf). A distinctive feature of relational learning is that it is able to exploit such patterns to create richer and more accurate models of relational domains.

When applying statistical models to incomplete knowledge graphs, it should be noted that the distribution of facts in such KGs can be skewed. For instance, KGs that are derived from Wikipedia will inherit the skew that exists in distribution of facts in Wikipedia itself[8] . Statistical models as discussed in the following sections can be affected by such biases in the input data and need to be interpreted accordingly.

C. Types of SRL Models

As we discussed, the presence or absence of certain triples in relational data is correlated with (i.e., predictive of) the presence or absence of certain other triples. In other words, the random variables $y_{ijk}$ are correlated with each other. We will discuss three main ways to model these correlations:

M1) Assume all $y_{ijk}$ are conditionally independent given latent features associated with subject, object and relation type and additional parameters (latent feature models)
M2) Assume all $y_{ijk}$ are conditionally independent given observed graph features and additional parameters (graph feature models)
M3) Assume all $y_{ijk}$ have local interactions (Markov Random Fields)

In what follows we will mainly focus on M1 and M2 and their combination; M3 will be the topic of Section VIII.

The model classes M1 and M2 predict the existence of a triple $x_{ijk}$ via a score function $f\left(x_{ijk};\Theta\right)$ which represents the model’s confidence that a triple exists given the parameters $\Theta$. The conditional independence assumptions of M1 and M2 allow the probability model to be written as follows:

[math]\displaystyle{ \displaystyle P\left(\mathbf{\underline{Y}}\vert \mathcal{D}, \Theta\right)=\prod_{i=1}^{N_e}\prod_{j=1}^{N_e}\prod_{k=1}^{N_r}\mathrm{Ber}\left(y_{ijk}\vert \sigma\left(f\left(x_{ijk}, \Theta \right)\right)\right) }[/math] (1)

where $\sigma(u) = 1/(1 +e^{-u})$ is the sigmoid (logistic) function, and

[math]\displaystyle{ \mathrm{Ber}(y\vert P)= \begin{cases} p, & \text{if } y=1 \\ 1-p, & \text{if} y=0 \end{cases} }[/math] (2)

is the Bernoulli distribution. We will refer to models of the form Equation (1) as probabilistic models. In addition to probabilistic models, we will also discuss models which optimize $f(\cdot)$ under other criteria, for instance models which maximize the margin between existing and non-existing triples. We will refer to such models as score-based models. If desired, we can derive probabilities for score-based models via Platt scaling [61].

There are many different methods for defining $f(\cdot)$. In the following Sections IV to Sections VI and VIII we will discuss different options for all model classes. In Section VII we will furthermore discuss aspects of how to train these models on knowledge graphs.

IV. LATENT FEATURE MODELS

In this section, we assume that the variables $y_{ijk}$ are conditionally independent given a set of global latent features and parameters, as in Equation 1. We discuss various possible forms for the score function $f (x; \Theta)$ below. What all models have in common is that they explain triples via latent features of entities (This is justified via various theoretical arguments [62]). For instance, a possible explanation for the fact that Alec Guinness received the Academy Award is that he is a good actor. This explanation uses latent features of entities (being a good actor) to explain observable facts (Guinness receiving the Academy Award). We call these features “latent” because they are not directly observed in the data. One task of all latent feature models is therefore to infer these features automatically from the data.

In the following, we will denote the latent feature representation of an entity $e_i$ by the vector $\mathbf{e}_i \in \R^{H_e}$ where $H_e$ denotes the number of latent features in the model. For instance, we could model that Alec Guinness is a good actor and that the Academy Award is a prestigious award via the vectors

[math]\displaystyle{ \mathbf{e}_{Guinness}=\begin{bmatrix}0.9\\0.2\end{bmatrix}, \quad \mathbf{e}_{Academy\;Award}=\begin{bmatrix}0.2\\0.8\end{bmatrix} }[/math]

where the component $e_{i1}$ corresponds to the latent feature Good Actor and $e_{i2}$ correspond to Prestigious Award. (Note that, unlike this example, the latent features that are inferred by the following models are typically hard to interpret.)

The key intuition behind relational latent feature models is that the relationships between entities can be derived from interactions of their latent features. However, there are many possible ways to model these interactions, and many ways to derive the existence of a relationship from them. We discuss several possibilities below. See Table III for a summary of the notation.

Relational data
Symbol Meaning
$N_e$ Number of entities
$N_r$ Number of relations
$N_d$ Number of training examples
$e_i$ $i$-th entity in the dataset (e.g., LeonardNimoy)
$r_k$ $k$-th relation in the dataset (e.g., bornIn)
$\mathcal{D}^{+}$ Set of observed positive triples
$\mathcal{D}^{-}$ Set of observed negative triples
Probabilistic Knowledge Graphs
Symbol Meaning Size
$\mathbf{\underline{Y}}$ (Partially observed) labels for all triples $N_e \times N_e \times N_r$
$\mathbf{\underline{F}}$ Score for all possible triples $N_e \times N_e \times N_r$
$\mathbf{Y}_k$ Slice of $\mathbf{\underline{Y}}$ for relation $r_k$ $N_e \times N_e$
$\mathbf{F}_k$ Slice of $\mathbf{\underline{F}}$ for relation $r_k$ $N_e \times N_e$
Graph and Latent Feature Models
Symbol Meaning
$\phi_{ijk}$ Feature vector representation of triple $\left(e_i, r_k, e_j\right)$
$\mathbf{w}k $ Weight vector to derive scores for relation $k$
$\Theta$ Set of all parameters of the model
$\sigma(\cdot)$ Sigmoid (logistic) function
Latent Feature Models
Symbol Meaning Size
$H_e$ Number of latent features for entities  
$H_r$ Number of latent features for relations  
$\mathbf{e}_i$ Latent feature representation. of entity $e_i$ $H_e$
$\mathbf{r}_k$ Latent feature representation of relation $r_k$ $H_r$
$H_a$ Size of $\mathbf{h}_a$ layer  
$H_b$ Size of $\mathbf{h}_b$ layer  
$H_c$ Size of $\mathbf{h}_c$ layer  
$\mathbf{E}$ Entity embedding matrix $N_e\times H_e$
$\mathbf{W}_k$ Bilinear weight matrix for relation $k$ $H_e\times H_e$
$\mathbf{A}_k$ Linear feature map for pairs of entities for relation $r_k$ $\left(2H_e\right)\times H_a$
$\mathbf{C}$ Linear feature map for triples $\left(2H_e+H_r\right)\times H_c$
TABLE III

SUMMARY OF THE NOTATION.

A. RESCAL: A Bilinear Model

RESCAL [63, 64, 65] is a relational latent feature model which explains triples via pairwise interactions of latent features. In particular, we model the score of a triple $x_{ijk}$ as

[math]\displaystyle{ f^{RESCAL}_{ijk}:=\mathbf{e}_i^{\top}\mathbf{W}_k\mathbf{e}_j =\displaystyle \sum_{a=1}^{H_e} \sum_{b=1}^{H_e} w_{abk}e_{ia}e_{jb} }[/math] (3)

where $\mathbf{W}_k \in \R^{H_e\times H_e}$ is a weight matrix whose entries $w_{abjk}$ specify how much the latent features $a$ and $b$ interact in the $k$-th relation. We call this a bilinear model, since it captures the interactions between the two entity vectors using multiplicative terms. For instance, we could model the pattern that good actors are likely to receive prestigious awards via a weight matrix such as

[math]\displaystyle{ \mathbf{W}_{receiveAward}=\begin{bmatrix}0.1&0.9\\0.1&0.1\end{bmatrix}, \quad \mathbf{e}_{Academy\;Award}=\begin{bmatrix}0.2\\0.8\end{bmatrix} }[/math]

In general, we can model block structure patterns via the magnitude of entries in $\mathbf{W}_k$, while we can model homophily patterns via the magnitude of its diagonal entries. Anti-correlations in these patterns can be modeled via negative entries in $\mathbf{W}_k$.

Hence, in Equation (3) we compute the score of a triple $x_{ijk}$ via the weighted sum of all pairwise interactions between the latent features of the entities $e_i$ and $e_j$. The parameters of the model are $\Theta = \{\{e_i\}^{N_e}, \{\mathbf{W}_k,\}^{N_r}_{k=1} \}$. During training we jointly learn the latent representations of entities and how the latent features interact for particular relation types.

In the following, we will discuss further important properties of the model for learning from knowledge graphs.

Relational learning via shared representations: In equation (3), entities have the same latent representation regardless of whether they occur as subjects or objects in a relationship. Furthermore, they have the same representation over all different relation types. For instance, the $i$-th entity occurs in the triple $x_{ijk}$ as the subject of a relationship of type $k$, while it occurs in the triple $x_{piq}$ as the object of a relationship of type $q$. However, the predictions $f_{ijk} = \mathbf{e}_i^{\top} \mathbf{W}_k\mathbf{e}_j$ and $f_{piq} = \mathbf{e}_p^{\top} \mathbf{W}_a\mathbf{e}_i$ both use the same latent representation $\mathbf{e}_i$ of the $i$-th entity. Since all parameters are learned jointly, these shared representations permit to propagate information between [[triple]s via the latent representations of entities and the weights of relations. This allows the model to capture global dependencies in the data.

Semantic embeddings: The shared entity representations in RESCAL capture also the similarity of entities in the relational domain, i.e., that entities are similar if they are connected to similar entities via similar relations [65]. For instance, if the representations of $\mathbf{e}_i$ and $\mathbf{e}_p$ are similar, the predictions $f_{ijk}$ and $f_{pjk}$will have similar values. In return, entities with many similar observed relationships will have similar latent representations. This property can be exploited for entity resolution and has also enabled large-scale hierarchical clustering on relational data [ 63, 64]. Moreover, since relational similarity is expressed via the similarity of vectors, the latent representations $\mathbf{e}_i$ can act as proxies to give non-relational machine learning algorithms such as k-means or kernel methods access to the similarity of entities.

Connection to tensor factorization: RESCAL is similar to methods used in recommendation systems [66], and to traditional tensor factorization methods [67]. In matrix notation, Equation (3) can be written compactly as as $\mathbf{F}k = \mathbf{EW}_k\mathbf{E}^{\top}$, where $\mathbf{F}k \in \R^{N_e\times N_e}$ is the matrix holding all scores for the $k$-th relation and the $i$-th row of $\mathbf{E} \in \R^{N_e\times H_e}$ holds the latent representation of $\mathbf{e}_i$. See Figure 4 for an illustration. In the following, we will use this tensor representation to derive a very efficient algorithm for parameter estimation.

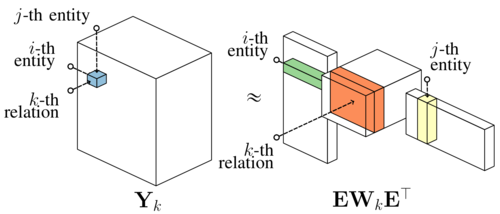
2016 AReviewofRelationalMachineLearn-Fig4.png
Figure 4: RESCAL as a tensor factorization of the adjacency tensor $\mathbf{Y}$.

Fitting the model: If we want to compute a probabilistic model, the parameters of RESCAL can be estimated by minimizing the log-loss using gradient-based methods such as stochastic gradient descent [68 ]. RESCAL can also be computed as a score-based model, which has the main advantage that we can estimate the parameters $\Theta$ very efficiently: Due to its tensor structure and due to the sparsity of the data, it has been shown that the RESCAL model can be computed via a sequence of efficient closed-form updates when using the squared-loss [63, 64]. In this setting, it has been shown analytically that a single update of $\mathbf{E}$ and $\mathbf{W}_k$ scales linearly with the number of entities $N_e$, and linearly with the number of relations $N_r$, and linearly with the number of observed triples, i.e., the number of non-zero entries in $\mathbf{\underline{Y}}$ [64]. We call this algorithm RESCAL-ALS[9]. In practice, a small number (say 30 to 50) of iterated updates are often sufficient for RESCAL-ALS to arrive at stable estimates of the parameters. Given a current estimate of $\mathbf{E}$, the updates for each $\mathbf{W}_k$ can be computed in parallel to improve the scalability on knowledge graphs with a large number of relations. Furthermore, by exploiting the special tensor structure of RESCAL, we can derive improved updates for RESCAL-ALS that compute the estimates for the parameters with a runtime complexity of $\mathcal{O} \left(H^3_e\right)$ for a single update (as opposed to a runtime complexity of $\mathcal{O} \left(H^5_e\right)$ for naive updates) [65, 69]. In summary, for relational domains that can be explained via a moderate number of latent features, RESCAL-ALS is highly scalable and very fast to compute. For more detail on RESCAL-ALS see also Equation (26) in Section VII.

Decoupled Prediction: In Equation (3), the probability of[single relationship is computed via simple matrix-vector products in $\mathcal{O} \left(H^2_e\right)$ time. Hence, once the parameters have been estimated, the computational complexity to predict the score of a triple depends only on the number of latent features and is independent of the size of the graph. However, during parameter estimation, the model can capture global dependencies due to the shared latent representations.

Relational learning results: RESCAL has been shown to achieve state-of-the-art results on a number of relational learning tasks. For instance, [63] showed that RESCAL provides comparable or better relationship prediction results on a number of small benchmark datasets compared to Markov Logic Networks (with structure learning) [70], the Infinite (Hidden) Relational model [71, 72], and Bayesian Clustered Tensor Factorization [73]. Moreover, RESCAL has been used for link prediction on entire knowledge graphs such as YAGO and DBpedia [64, 74]. Aside from link prediction, RESCAL has also successfully been applied to SRL tasks such as entity resolution and link-based clustering. For instance, RESCAL has shown state-of-the-art results in predicting which authors, publications, or publication venues are likely to be identical in publication databases [63, 65]. Furthermore, the semantic embedding of entities computed by RESCAL has been exploited to create taxonomies for uncategorized data via hierarchical clusterings of entities in the embedding space [75].

B. Other Tensor Factorization Models

Various other tensor factorization methods have been explored for learning from knowledge graphs and multi-relational data. [76, 77] factorized adjacency tensors using the CP tensor decomposition to analyze the link structure of Web pages and Semantic Web data respectively. [78] applied pairwise interaction tensor factorization [79] to predict triples in knowledge graphs. [80] applied factorization machines to large uni-relational datasets in recommendation settings. [81] proposed a tensor factorization model for knowledge graphs with a very large number of different relations.

It is also possible to use discrete latent factors. [82] proposed Boolean tensor factorization to disambiguate facts extracted with OpenIE methods and applied it to large datasets [83]. In contrast to previously discussed factorizations, Boolean tensor factorizations are discrete models, where adjacency tensors are decomposed into binary factors based on Boolean algebra.

C. Matrix Factorization Methods

Another approach for learning from knowledge graphs is based on matrix factorization, where, prior to the factorization, the adjacency tensor $\mathbf{\underline{Y}} \in \R^{Ne \times\;N_e\times\;N_r}$ is reshaped into a matrix $\mathbf{Y} \in \R^{Ne^2\times\;N_r}$ by associating rows with subject-object pairs $\left(e_i,e_j\right)$ and columns with relations $r_k$ (cf. 84, 85]), or into a matrix $\mathbf{Y} \in \R^{Ne \times\;N_e\;N_r}$ by associating rows with subjects $e_i$ and columns with relation / objects $(r_k, e_j)$ (cf. [86, 87]). Unfortunately, both of these formulations lose information compared to tensor factorization. For instance, if each subjectobject pair is modeled via a different latent representation, the information that the relationships $y_{ijk}$, and $y_{pjq}$share the same object is lost. It also leads to an increased memory complexity, since a separate latent representation is computed for each pair of entities, requiring $\mathcal{O} \left(N_e^2 H,_e + N_r H_e\right)$ parameters (compared to $\mathcal{O}\left (N_eH_e + N_r H_e^2\right)$ parameters for RESCAL).

D. Multi-Layer Perceptrons

We can interpret RESCAL as creating composite representations of triples and predicting their existence from this representation. In particular, we can rewrite RESCAL as

[math]\displaystyle{ f^{RESCAL}_{ijk}:=\mathbf{w}^{\top}_k\phi_{ij}^{RESCAL} }[/math] (4)
[math]\displaystyle{ \phi^{RESCAL}_{ij}:=\mathbf{e}_j\otimes \mathbf{e}_i }[/math] (5)

where $\mathbf{w}_k = vec \left(\mathbf{W}_k\right)$. Equation (4) follows from Equation (3) via the equality $vec\left(\mathbf{AXB}\right) = \left(\mathbf{B}^{top} \mathbf{A}\right) vec(\mathbf{X})$. Hence, RESCAL represents pairs of entities $\left(e_i,e_j\right)$ via the tensor product of their latent feature representations (Equation (5)) and predicts the existence of the $triple$ $x_{ijk}$ from $\phi_{ij}$ via $\mathbf{w}_z$ (Equation (4)). See also Figure 5a. For a further discussion of the tensor product to create composite latent representations please see [88, 89, 90].

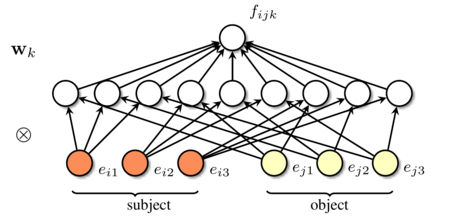
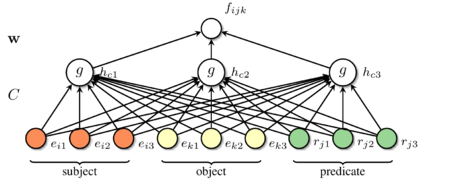
2016 AReviewofRelationalMachineLearn-Fig5a.png 2016 AReviewofRelationalMachineLearn-Fig5b.png
(a) RESCAL (b) ER-MLP
Figure 5: Visualization of RESCAL and the ER-MLP model as Neural Networks. Here, $H_e =H_r= 3$ and $H_a= 3$. Note, that the inputs are latent features. The symbol $g$ denotes the application of the function $g(\cdot)$.

Since the tensor product explicitly models all pairwise interactions, RESCAL can require a lot of parameters when the number of latent features are large (each matrix $\mathbf{W}_e$, has $H_e^2$ entries). This can, for instance, lead to scalability problems on knowledge graphs with a large number of relations.

In the following we will discuss models based on multilayer perceptrons (MLPs), also known as feedforward neural networks. In the context of multidimensional data they can be referred to a multiway neural networks. This approach allows us to consider alternative ways to create composite triple representations and to use nonlinear functions to predict their existence.

In particular, let us define the following E-MLP model (E for entity):

[math]\displaystyle{ f^{E-MLP}_{ijk}:=\mathbf{w}^{\top}_k\mathbf{g}\left(\mathbf{h}^a_{ijk}\right) }[/math] (6)
[math]\displaystyle{ \mathbf{h}^a_{ijk}\:=\mathbf{A}_k^{top} \phi_{ij}^{E-MLP} }[/math] (7)
[math]\displaystyle{ \phi_{ij}^{E-MLP}:=\big[ \mathbf{e}_i; \mathbf{e}_j\big] }[/math] (8)

where $\mathbf{g(u)} = \big[g(u_1),g(u_2),\cdots\big]$ is the function $g$ applied element-wise to vector $\mathbf{u}$; one often uses the nonlinear function $g(u) = tanh(u)$.

Here $\mathbf{h}_a$ is an additive hidden layer, which is deriving by adding together different weighed components of the entity representations. In particular, we create a composite representation $\phi^{E-MLP}_{ij}=\big[ \mathbf{e}_i;\mathbf{e}_j\big] \in \R^{2H_a}$ via the concatenation ofe_i ande_i. However, concatenation alone does not consider any interactions between the latent features of $e_i$ and $e_j$. For this reason, we add a (vector-valued) hidden layer $h$, of size $H_a$, from which the final prediction is derived via $\mathbf{w}_k^{top} \mathbf{g}(\mathbf{h}_a)$. The important difference to tensor-product models like RESCAL is that we learn the interactions of latent features via the matrix A; (Equation (7)), while the tensor product considers always all possible interactions between latent features. This adaptive approach can reduce the number of required parameters significantly, especially on datasets with a large number of relations.

One disadvantage of the E-MLP is that it has to define a vector $\mathbf{w}_k$, and a matrix $\mathbf{A}_k$, for every possible relation, which requires $H_a + (H_a \times 2H_e)$ parameters per relation. An alternative is to embed the relation itself, using a $H_{r^{-}}$ dimensional vector $\mathbf{r}_k$. We can then define

[math]\displaystyle{ f^{E-MLP}_{ijk}:=\mathbf{w}^{\top}_k\mathbf{g}\left(\mathbf{h}^c_{ijk}\right) }[/math] (9)
[math]\displaystyle{ \mathbf{h}^c_{ijk}\:=\mathbf{C}_k^{top} \phi_{ijk}^{E-MLP} }[/math] (10)
[math]\displaystyle{ \phi_{ijk}^{E-MLP}:=\big[ \mathbf{e}_i; \mathbf{e}_j;\mathbf{r}_k\big] }[/math] (11)

We call this model the ER-MLP, since it applies an MLP to an embedding of the entities and relations. Please note that ER-MLP uses a global weight vector for all relations. This model was used in the KV project (see Section IX), since it has many fewer parameters than the E-MLP (see Table V); the reason is that $\mathbf{C}$ is independent of the relation $k$.

It has been shown in &#9191] that MLPs can learn to put “semantically similar” words close by in the embedding space, even if they are not explicitly trained to do so. In [28], they show a similar result for the semantic embedding of relations using ER-MLP. For example, Table IV shows the nearest neighbors of latent representations of selected relations that have been computed with a 60 dimensional model on Freebase. Numbers in parentheses represent squared Euclidean distances. It can be seen that ER-MLP puts semantically related relations near each other. For instance, the closest relations to the children relation are parents, spouse, and birthplace.

Relation Nearest Neighbors
children parents (0.4) spouse (0.5) birth-place (0.8)
birth-date children (1.24) gender (1.25) parents (1.29)
edu-end[10] job-start (1.41) edu-start (1.61) job-end (1.74)
TABLE IV

SEMANTIC EMBEDDINGS OF KV-MLP ON FREEBASE

E. Neural Tensor Networks

We can combine traditional MLPs with bilinear models, resulting in what [92] calls a “neural tensor network” (NTN). More precisely, we can define the NTN model as follows:

[math]\displaystyle{ f^{E-MLP}_{ijk}:=\mathbf{w}^{\top}_k\mathbf{g}\left(\big[\mathbf{h}^a_{ijk};\mathbf{h}^b_{ijk}\big]\right) }[/math] (12)
[math]\displaystyle{ \mathbf{h}^a_{ijk}:=\mathbf{A}_k^{\top}\big[\mathbf{e}_i; \mathbf{e}_j;\mathbf{r}_k\big] }[/math] (13)
[math]\displaystyle{ \mathbf{h}^a_{ijk}:=\mathbf{A}_k^{\top}\big[\mathbf{e}_i\mathbf{B}_k^{1}\mathbf{e}_j ,\cdots, \mathbf{e}_i\mathbf{B}_k^{H_b}\mathbf{e}_j\big] }[/math] (14)

Here $\mathbf{\underline{B}}_k$, is a tensor, where the $\ell$-th slice $\mathbf{B}_k^{\ell}$ has size $H_e \times H_e$, and there are $H_b$ slices. We call $\mathbf{h}_{ijk}^b$ a bilinear hidden layer, since it is derived from a weighted combination of multiplicative terms.

 NTN is a generalization of the RESCAL approach, as we explain in Section XII-A. Also, it uses the additive layer from the E-MLP model. However, it has many more parameters than the E-MLP or RESCAL models. Indeed, the results in [95] and [28] both show that it tends to overfit, at least on the (relatively small) datasets uses in those papers.

F. Latent Distance Models

Another class of models are latent distance models (also known as latent space models in social network analysis), which derive the probability of relationships from the distance between latent representations of entities: entities are likely to be in a relationship if their latent representations are close according to some distance measure. For uni-relational data, [96] proposed this approach first in the context of social networks by modeling the probability of a relationship $x_{ij}$ via the score function $f (e_i,e_j) = - d (\mathbf{e}_i,\mathbf{e}_j)$ where $d (\cdot., \cdots)$ refers to an arbitrary distance measure such as the Euclidean distance.

The structured embedding (SE) model [93] extends this idea to multi-relational data by modeling the score of a triple $x_{ijk}$ as:

[math]\displaystyle{ f^{SE}_{ijk}:= -\parallel\;\mathbf{A}_k^{s}\mathbf{e}_i -\mathbf{A}_k^{0}\mathbf{e}_j\parallel=-\parallel\mathbf{h}^a_{ijk}\parallel_1 }[/math] (15)

where $\mathbf{A}_k = \big[\mathbf{A}_k^{s}; -\mathbf{A}_k^{0}\big]$. In Equation (15) the matrices $\mathbf{A}_k^{0}$. transform the global latent feature representations of entities to model relationships specifically for the $k$-th relation. The transformations are learned using the ranking loss in a way such that pairs of entities in existing relationships are closer to each other than entities in non-existing relationships.

To reduce the number of parameters over the SE model, the TransE model [94] translates the latent feature representations via a relation-specific offset instead of transforming them via matrix multiplications. In particular, the score of a triple $x_{ijk}$ is defined as:

[math]\displaystyle{ f^{TransE}_{ijk}:= -d \left(\mathbf{e}_i+\mathbf{r}_k, \mathbf{e}_j\right) }[/math] (16)

This model is inspired by the results in[ 91], who showed that some relationships between words could be computed by their vector difference in the embedding space. As noted in [95], under unit-norm constraints on $\mathbf{e}_i$, $\mathbf{e}_j$; and using the squared Euclidean distance, we can rewrite Equation (16) as follows:

[math]\displaystyle{ f^{TransE}_{ijk}:= - \left(2\mathbf{r}_k^{\top} \left(\mathbf{e}_i - \mathbf{e}_j\right)- 2\mathbf{e}_j^{\top}\mathbf{e}_j + \parallel \mathbf{r}_k\parallel_2^2 \right) }[/math] (17)

Furthermore, if we assume $\mathbf{A}_k=[\mathbf{r}_k; - \mathbf{r}_k]$, so that $h^a_{ijk}=[\mathbf{r}_k; - \mathbf{r}_k]^T[(\mathbf{e}_i ; \mathbf{e}]=\left(\mathbf{r}_k^T\mathbf{e}_i - \mathbf{e}_j\right)$ and $\mathbf{\underline{B}} = \mathbf{I}$, so that $ $h^a_{ijk}=e_i^Te_j$, then we can rewrite this model as follows:

[math]\displaystyle{ f^{TransE}_{ijk}:= - \left(2h_{ijk}^a - 2 h_{ijk}^b + \parallel\mathbf{r}_k\parallel_2^2\right)- 2\mathbf{e}_j^{\top}\mathbf{e}_j + \parallel \mathbf{r}_k\parallel_2^2 }[/math] (18)

==== G. Comparison Of Models ====

Table V summarizes the different models we have discussed. A natural question is: which model is best? [28] showed that the ER-MLP model outperformed the NTN model on their particular dataset. [95] performed more extensive experimental comparison of these models, and found that RESCAL (called the bilinear model) worked best on two link prediction tasks. However, clearly the best model will be dataset dependent.

Method $f_{ijk}$ $\mathbf{A}_k$ $\mathbf{C}$ $\mathbf{\underline{B}}_k$ Num. Parameters
RESCAL [64] $\mathbf{w}_k^{\top} \mathbf{h}^b_{ijk}$ - - $[\delta_{1,1},\cdots, \delta_{H_e,H_e}]$ $N_rH^2_e+ N_eH_e$
E-MLP [92] $\mathbf{w}_k^{\top}\mathbf{g} \left(\mathbf{h}^a_{ijk}\right)$ $\big[\mathbf{A}^s_k ; \mathbf{A}^o_k \big]$ - - $N_r\left(H_a + H_a \times\; 2H_e\right)+N_eH_e$
ER-MLP [28] $\mathbf{w}_k^{\top}\mathbf{g} \left(\mathbf{h}^c_{ijk}\right)$ - $\mathbf{C}$ - $H_c + H_c \times\; \left(2H_e + H_r\right) + N_rH_r + N_eH_e$
NTN [92] $\mathbf{w}_k^{\top}\mathbf{g} \left(\big[\mathbf{h}^a_{ijk}; \mathbf{h}^b_{ijk}\big]\right)$ $\big[\mathbf{A}^s_k ; \mathbf{A}^o_k \big]$ - $\big[\mathbf{B}^1_k ,\cdots,\mathbf{B}^{H_b}_k \big]$ $N^2_e H_b + N_r\left(H_b + H_a\right) + 2N_rH_eH_a + N_eH_e$
Structured Embeddings [93] $-\parallel\mathbf{h}^a_{ijk}\parallel_1$ $\big[\mathbf{A}^s_k ;- \mathbf{A}^o_k \big]$ - $-$ $2\;N_rH_eH_a + N_eH_e$
TransE [94] $-\left(2\;h^a_{ijk}-2\;h^b_{ijk}+\parallel\mathbf{r}_k\parallel_2^2\right)$ $\big[\mathbf{r}_k;-\mathbf{r}_k\big]$ - $\mathbf{I}$ $N_rH_e + N_eH_e$
TABLE V

SUMMARY OF THE LATENT FEATURE MODELS $\mathbf{h}_a$, $\mathbf{h}_b$ AND $\mathbf{h}_c$ ARE HIDDEN LAYERS OF THE NEURAL NETWORK; SEE TEXT FOR DETAILS

V. GRAPH FEATURE MODELS

In this section, we assume that the existence of an edge can be predicted by extracting features from the observed edges in the graph. For example, due to social conventions, parents of a person are often married, so we could predict the triple $(John,\; marriedTo,\;Mary)$ from the existence of the path $John \xrightarrow{ParentOf}Anne \xleftarrow{ParentOf}Mary$, representing a common child. In contrast to latent feature models, this kind of reasoning explains triples directly from the observed triples in the knowledge graph. We will now discuss some models of this kind.

A. Similarity Measures For Uni-Relational Data

Observable graph feature models are widely used for link prediction in graphs that consist only of a single relation, e.g., social network analysis (friendships between people), biology (interactions of proteins), and Web mining (hyperlinks between Web sites). The intuition behind these methods is that similar entities are likely to be related (homophily) and that the similarity of entities can be derived from the neighborhood of nodes or from the existence of paths between nodes. For this purpose, various indices have been proposed to measure the similarity of entities, which can be classified into local, global, and quasi-local approaches [97].

 Local similarity indices such as Common Neighbors, the Adamic-Adar index [98] or Preferential Attachment [99] derive the similarity of entities from their number of common neighbors or their absolute number of neighbors. Local similarity indices are fast to compute for single relationships and scale well to large knowledge graphs as their computation depends only on the direct neighborhood of the involved entities. However, they can be too localized to capture important patterns in relational data and cannot model long-range or global dependencies.

 Global similarity indices such as the Katz index [100] and the Leicht-Holme-Newman index [101] derive the similarity of entities from the ensemble of all paths between entities, while indices like Hitting Time, Commute Time, and PageRank [102] derive the similarity of entities from random walks on the graph. Global similarity indices often provide significantly better predictions than local indices, but are also computationally more expensive [97, 56].

 Quasi-local similarity indices like the Local Katz index [56] or Local Random Walks [103] try to balance predictive accuracy and computational complexity by deriving the similarity of entities from paths and random walks of bounded length.

In Section V-C, we will discuss an approach that extends this idea of quasi-local similarity indices for uni-relational networks to learn from large multi-relational knowledge graphs.

B. Rule Mining and Inductive Logic Programming

Another class of models that works on the observed variables of a knowledge graph extracts rules via mining methods and uses these extracted rules to infer new links. The extracted rules can also be used as a basis for Markov Logic as discussed in Section VIII. For instance, ALEPH is an Inductive Logic Programming (ILP) system that attempts to learn rules from relational data via inverse entailment [104] (For more information on ILP see e.g.,[106 105, 3, 106]). AMIE is a rule mining system that extracts logical rules (in particular Horn clauses) based on their support in a knowledge graph [107, 108]. In contrast to ALEPH, AMIE can handle the open-world assumption of knowledge graphs and has shown to be up to three orders of magnitude faster on large knowledge graphs [108]. The basis for the Semantic Web is Description Logic and[109, 110, 111] describe approaches for logic oriented machine learning approaches in this context. Also to mention are data mining approaches for knowledge graphs as described in[112, 113, 114]. An advantage of rule-based systems is that they are easily interpretable as the model is given as a Set of logical rules. However, rules over observed variables cover usually only a subset of patterns in knowledge graphs (or relational data) and useful rules can be challenging to learn.

C. Path Ranking Algorithm

The Path Ranking Algorithm (PRA) [115, 116] extends the idea of using random walks of bounded lengths for predicting links in multi-relational knowledge graphs. In particular, let $\pi_L(i,j,k,t)$ denote a path of length $L$ of the form $e_i \xrightarrow{r_1} e_2\xrightarrow{r_2} e_3\cdots\xrightarrow{r_L}e_j$, where $t$ represents the sequence of edge types $t = (r_1,r_2,\cdots,r_L)$. We also require there to be a direct arc $e_i \xrightarrow{r_k}e_j$, representing the existence of a relationship of type $k$ from $e_i$ to $e_j$. Let $\Pi_L (i, j,k)$ represent the set of all such paths of length $L$, ranging over path types $t$. (We can discover such paths by enumerating all (type-consistent) paths from entities of type $e_i$ to entities of type $e_j$. If there are too many relations to make this feasible, we can perform random sampling.)

We can compute the probability of following such a path by assuming that at each step, we follow an outgoing link uniformly at random. Let $P\left(\pi_L,(i,j,k,t)\right)$ be the probability of this particular path; this can be computed recursively by a sampling procedure, similar to PageRank (see [116] for details). The key idea in PRA is to use these path probabilities as features for predicting the probability of missing edges. More precisely, define the feature vector

[math]\displaystyle{ \phi^{PRA}_{ijk}=\big[P(\pi):\pi\in\Pi_L(i,j,k) \big] }[/math] (19)

We can then predict the edge probabilities using logistic regression:

We can compute the probability of following such a path by assuming that at each step, we follow an outgoing link uniformly at random. Let $P\left(\pi_L,(i,j,k,t)\right)$ be the probability of this particular path; this can be computed recursively by a sampling procedure, similar to PageRank (see [116] for details). The key idea in PRA is to use these path probabilities as features for predicting the probability of missing edges. More precisely, define the feature vector

[math]\displaystyle{ f_{ijk}^{PRA}:=\mathbf{w}_k^{\top}phi^{PRA}_{ijk} }[/math] (20)

Interpretability: A useful property of PRA is that its model is easily interpretable. In particular, relation paths can be regarded as bodies of weighted rules — more precisely Horn clauses — where the weight specifies how predictive the body of the rule is for the head. For instance, Table VI shows some relation paths along with their weights that have been learned by PRA in the KV project (see Section IX) to predict which college a person attended, i.e., to predict triples of the form $(p,\; college,\; c)$. The first relation path in Table VI can be interpreted as follows: it is likely that a person attended a college if the sports team that drafted the person is from the same college. This can be written in the form of a Horn clause as follows:

[math]\displaystyle{ (p,\; college,\; c)\; \leftarrow\; (p, draftedBy, t) \;\wedge \; (t, school, c) }[/math] .

By using a sparsity promoting prior on $\mathbf{w}_k$, we can perform feature selection, which is equivalent to rule learning.

Relational learning results: PRA has been shown to outperform the ILP method FOIL [106] for link prediction in NELL 116. It has also been shown to have comparable performance to ER-MLP on link prediction in KV: PRA obtained a result of 0.884 for the area under the ROC curve, as compared to 0.882 for ER-MLP [28].

Relation Path F1 Prec Rec Weight
(draftedBy, school) 0.03 1.0 0.01 2.62
(sibling(s), sibling, education, institution) 0.05 0.55 0.02 1.88
(spouse(s), spouse, education, institution) 0.06 0.41 0.02 1.87
(parents, education, institution) 0.04 0.29 0.02 1.37
(children, education, institution) 0.05 0.21 0.02 1.85
(placeOfBirth, peopleBornHere, education) 0.13 0.1 0.38 6.4
(type, instance, education, institution) 0.05 0.04 0.34 1.74
(profession, peopleWithProf., edu., inst.) 0.04 0.03 0.33 2.19
TABLE VI

EXAMPLES OF PATHS LEARNED BY PRA ON FREEBASE TO PREDICT WHICH COLLEGE A PERSON ATTENDED

VI. COMBINING LATENT AND GRAPH FEATURE MODELS

It has been observed experimentally (see, e.g., [28]) that neither state-of-the-art relational latent feature models (RLFMs) nor state-of-the-art graph feature models are superior for learning from knowledge graphs. Instead, the strengths of latent and graph-based models are often complementary (see e.g., [117]), as both families focus on different aspects of relational data:

There has also been some theoretical work comparing these two approaches [118]. In particular, it has been shown that tensor factorization can be inefficient when relational data consists of a large number of strongly connected components. Fortunately, such “problematic” relations can often be handled efficiently via graph-based models. A good example is the $marriedTo$ relation: One marriage corresponds to a single strongly connected component, so data with a large number of marriages would be difficult to model with RLFMs. However, predicting $marriedTo$ links via graph-based models is easy: the existence of the triple $(John,\; marriedTo,\; Mary)$ can be simply predicted from the [existence of $(Mary,\; marriedTo,\; John)$, by exploiting the symmetry of the relation. If the $(Mary,\; marriedTo,\; John)$ edge is unknown, we can use statistical patterns, such as the existence of shared children.

Combining the strengths of latent and graph-based models is therefore a promising approach to increase the predictive performance of graph models. It typically also speeds up the training. We now discuss some ways of combining these two kinds of models.

A. Additive Relational Effects Model

[118] proposed the additive relational effects (ARE), which is a way to combine RLFMs with observable graph models. In particular, if we combine RESCAL with PRA, we get

[math]\displaystyle{ f^{RESCAL+PRA}_{ijk}=\mathbf{w}_k^{(1)\top}\phi_{ij}^{RESCAL}+\mathbf{w}_k^{(2)\top}\phi_{ij}^{RESCAL} }[/math] (21)

 ARE models can be trained by alternately optimizing the RESCAL parameters with the PRA parameters. The key benefit is now RESCAL only has to model the “residual errors” that cannot be modelled by the observable graph patterns. This allows the method to use much lower latent dimensionality, which significantly speeds up training time. The resulting combined model also has increased accuracy [118].

B. Other Combined Models

In addition to ARE, further models have been explored to learn jointly from latent and observable patterns on relational data. [84, 85] combined a latent feature model with an additive term to learn from latent and neighborhood-based information on multi-relational data, as follows[11]:

[math]\displaystyle{ f^{ADD}_{ijk}:=\mathbf{w}_{k,j}^{(1)\top}\phi_{i}^{SUB}+\mathbf{w}_{k,i}^{(2)\top}\phi_{j}^{OBJ}+\mathbf{w}_{k}^{(3)\top}\phi_{ijk}^{N} }[/math] (22)
[math]\displaystyle{ \phi_{ijk}^{N}:=\big[y_{ijk'}:k'\ne k \big] }[/math] (23)

Here, $\phi_u^{SUB}$ is the latent representation of entity $e_i$ as a subject and $phi_j^{OBJ}$ is the latent representation of entity $e_j$ as an object. The term $\phi_{ijk}^N$ captures patterns efficiently where the existence of a triple $y_{ijk'}$ is predictive of another triple $y_{ijk}$ between the same pair of entities (but of a different relation type). For instance, if Leonard Nimoy was born in Boston, it is also likely that he lived in Boston. This dependency between the relation types $bornIn$ and $livedIn$ can be modeled in Equation (23) by assigning a large weight to $w_{bornIn,\;livedIn}$

ARE and the models of [84] and [85] are similar in spirit to the model of [119], which augments SVD (ce., matrix factorization) of a rating matrix with additive terms to include local neighborhood information. Similarly, factorization machines [120] allow to combine latent and observable patterns, by modeling higher-order interactions between input variables via low-rank factorizations [78].

An alternative way to combine different prediction systems is to fit them separately, and use their outputs as inputs to another “fusion” system. This is called stacking[121]. For instance,[28] used the output of PRA and ER-MLP as scalar features, and learned a final “fusion” layer by training a binary classifier. Stacking has the advantage that it is very flexible in the kinds of models that can be combined. However, it has the disadvantage that the individual models cannot cooperate, and thus any individual model needs to be more complex than in a combined model which is trained jointly. For example, if we fit RESCAL separately from PRA, we will need a larger number of latent features than if we fit them jointly.

VII. TRAINING SRL MODELS ON KNOWLEDGE GRAPHS

In this section we discuss aspects of training the previously discussed models that are specific to knowledge graphs, such as how to handle the open-world assumption of knowledge graphs, how to exploit sparsity, and how to perform model selection.

A. Penalized Maximum Likelihood Training

Let us assume we have a set of $Nd$ observed triples and let the $n$-th triple be denoted by $x^n$. Each observed triple is either true (denoted $y^n = 1$) or false (denoted $y^n = 0$). Let this labeled dataset be denoted by $\mathcal{D} = \{\left(x^n, y^n\right) \vert\; n =1,\cdots, N_d\}$. Given this, a natural way to estimate the parameters $\Theta$ is to compute the maximum a posteriori (MAP) estimate:

[math]\displaystyle{ \displaystyle \underset{\Theta}{\mathrm{max}}\sum_{n=1}^{N_d}\log\mathrm{Ber}\left(y^n\vert\;\sigma\left(f\left(x^n;\Theta\right)\right)\right)+\log p\left(\boldsymbol{\Theta}\vert\lambda\right) }[/math] (24)

where $\lambda$ controls the strength of the prior. (If the prior is uniform, this is equivalent to maximum likelihood training.) We can equivalently state this as a regularized loss minimization problem:

[math]\displaystyle{ \displaystyle \underset{\Theta}{\mathrm{min}}\sum_{n=1}^{N}\mathcal{L}\left(\sigma\left(f\left(x^n;\Theta\right)\right), y^n\right)+\lambda\;\mathrm{reg}\left(\boldsymbol{\Theta}\right) }[/math] (25)

where $\mathcal{L}(p,y) = -\log\mathrm{Ber}(y\vert P)$ is the log loss function. Another possible loss function is the squared loss, $\mathcal{L}(p, y) = (p — y)^2$. Using the squared loss can be especially efficient in combination with a closed-world assumption (CWA). For instance, using the squared loss and the CWA, the minimization problem for RESCAL becomes

[math]\displaystyle{ \displaystyle \underset{\mathbf{E}\{\mathbf{W}_k\}}{\mathrm{min}}\sum_k\parallel\mathbf{Y}_k-\mathbf{EW}_k\mathbf{E}^{\top}\parallel^2_F+\lambda_1\parallel\mathbf{E}\parallel^2_F+\lambda_2\sum_k\parallel\mathbf{W}_k\parallel^2_F }[/math] (26)

where $\lambda_1, \lambda_2 \ge 0$ control the degree of regularization. The main advantage of Equation (26) is that it can be optimized via RESCAL-ALS, which consists of a sequence of very efficient, closed-form updates whose computational complexity depends only on the non-zero entries in $\mathbf{Y}$ [63, 64]. We discuss some other loss functions below.

B. Where Do The Negative Examples Come From?

One important question is where the labels $y^2$ come from. The problem is that most knowledge graphs only contain positive training examples, since, usually, they do not encode false facts. Hence $y^n = 1$ for all $\left(x^n, y^n\right) \in \mathcal{D}$. To emphasize this, we shall use the notation $\mathcal{D}^+$ to represent the observed positive (true) triples: $\mathcal{D}^+ = \{x^n \in \mathcal{D} | y^n = 1\}. Training on all-positive data is tricky, because the model might easily over generalize.

One way around this is as to make a closed world assumption and assume that all (type consistent) triples that are not in $\mathcal{D}^+$ are false. We will denote this negative set as $\mathcal{D}^- = \{x^2 \in \mathcal{D} |y^2 = 0\}$. However, for incomplete knowledge graphs this assumption will be violated. Moreover, $\mathcal{D}^-$ might be very large, since the number of false facts is much larger than the number of true facts. This can lead to scalability issues in training methods that have to consider all negative examples.

An alternative approach to generate negative examples is to exploit known constraints on the structure of a knowledge graph: Type constraints for predicates (persons are only married to persons), valid value ranges for attributes (the height of humans is below 3 meters), or functional constraints such as mutual exclusion (a person is born exactly in one city) can all be used for this purpose. Since such examples are based on the violation of hard constraints, it is certain that they are indeed negative examples. Unfortunately, functional constraints are scarce and negative examples based on type constraints and valid value ranges are usually not sufficient to train useful models: While it is relatively easy to predict that a person is married to another person, it is difficult to predict to which person in particular. For the latter, examples based on type constraints alone are not very informative. A better way to generate negative examples is to “perturb” true triples. In particular, let us define

[math]\displaystyle{ \mathcal{D}^- = \{\left(e_{\ell}, r_k, e_j\right) | e_i \ne e_{\ell} \wedge \left(e_i,r_k,e_j\right) \in \mathcal{D}^+\} \cup \{\left(e_i, r_,k e_{\ell}\right) | e_j \ne e_{\ell} \wedge \left(e_i,r_k,e_j\right) \in \mathcal{D}^+\} }[/math]

To understand the difference between this approach and the CWA (where we assumed all valid unknown triples were false), let us consider the example in Figure 1. The CWA would generate “good” negative triples such as $(LeonardNimoy,\; starredIn,\; StarWars)$, $(AlecGuinness,\; starredIn,\; StarTrek)$, etc., but also type-consistent but “irrelevant” negative triples such as $(BarackObama,\; starredIn,\; StarTrek)$, etc. (We are assuming (for the sake of this example) there is a type $Person$ but not a type $Actor$.) The second approach (based on perturbation) would not generate negative triples such as $(BarackObama,\; starredIn,\; StarTrek)$, since $BarackObama$ does not participate in any $starredIn$ events. This reduces the size of $D^-$, and encourages it to focus on “plausible” negatives. (An even better method, used in Section IX, is to generate the candidate triples from text extraction methods run on the Web. Many of these triples will be false, due to extraction errors, but they define a good set of “plausible” negatives.)

Another option to generate negative examples for training is to make a local-closed world assumption (LCWA) [107, 28], in which we assume that a KG is only locally complete. More precisely, if we have observed any triple for a particular subject-predicate pair $e_i$, $r_k$, then we will assume that any non-existing triple $\left(e_i,rk,\cdot\right)$ is indeed false and include them in $\mathcal{D}^-$. (The assumption is valid for functional relations, such as $bornIn$, but not for set-valued relations, such as $starredIn$). However, if we have not observed any triple at all for the pair $e_i$, $r_k$, we will assume that all triples $\left(e_i,r_k,\cdot\right)$ are unknown and not include them in $\mathcal{D}^-$.

C. Pairwise Loss Training

Given that the negative training examples are not always really negative, an alternative approach to likelihood training is to try to make the probability (or in general, some scoring function) to be larger for true triples than for assumed-to-be-false triples. That is, we can define the following objective function:

[math]\displaystyle{ \displaystyle \underset{\Theta}{\mathrm{min}}\sum_{x^+\in\mathcal{D}^+}\sum_{x^-\in\mathcal{D}^-}\mathcal{L}\left(f\left(x^+;\Theta\right), f\left(x^-;\Theta\right)+\lambda\;\mathrm{reg}\Theta\right) }[/math] (27)

where $\mathcal{L}(f, f’$) is a margin-based ranking loss function such as

[math]\displaystyle{ \mathcal{L}\left(f,f'\right)=\mathrm{max}\left(1+f'-f,\; 0\right) }[/math] (28)

This approach has several advantages. First, it does not assume that negative examples are necessarily negative, just that they are “more negative” than the positive ones. Second, it allows the $f(\cdot)$ function to be any function, not just a probability (but we do assume that larger f values mean the triple is more likely to be correct).

This kind of objective function is easily optimized by stochastic gradient descent (SGD) [122]: at each iteration, we just sample one positive and one negative example. SGD also scales well to large datasets. However, it can take a long time to converge. On the other hand, as discussed previously, some models, when combined with the squared loss objective, can be optimized using alternating least squares (ALS), which is typically much faster.

D. Model Selection

Almost all models discussed in previous sections include one or more user-given parameters that are influential for the model’s performance (e.g., dimensionality of latent feature models, length of relation paths for PRA, regularization parameter for penalized maximum likelihood training). Typically, crossvalidation over random splits of $\mathcal{D}$ into training -, validation -, and test-sets is used to find good values for such parameters without overfitting (for more information on model selection in machine learning see e.g., [123]). For link prediction and entity resolution, the area under the ROC curve (AUC-ROC) or the area under the precision-recall curve (AUC-PR) are good evaluation criteria. For data with a large number of negative examples (as it is typically the case for knowledge graphs), it has been shown that AUC-PR can give a clearer picture of an algorithm’s performance than AUC-ROC [124]. For entity resolution, the mean reciprocal rank (MRR) of the correct entity is an alternative evaluation measure.

VIII. MARKOV RANDOM FIELDS

In this section we drop the assumption that the random variables $y_{ijk}$ in $\mathbf{\underline{Y}}$ are conditionally independent. However, in the case of relational data and without the conditional independence assumption, each $y_{ijk}$ can depend on any of the other $N_e\times\; N_e\; N_r - 1$ random variables in $\mathbf{Y}$. Due to this enormous number of possible dependencies, it becomes quickly intractable to estimate the joint distribution $P(\mathbf{\underline{Y}})$ without further constraints, even for very small knowledge graphs. To reduce the number of potential dependencies and arrive at tractable models, in this section we develop template based graphical models that only consider a small fraction of all possible dependencies.

(See [125] for an introduction to graphical models.)

A. Representation

Graphical models use graphs to encode dependencies between random variables. Each random variable (in our case, a possible fact $y_{ijk}$) is represented as a node in the graph, while each dependency between random variables is represented as an edge. To distinguish such graphs from knowledge graphs, we will refer to them as dependency graphs. It is important to be aware of their key difference: while knowledge graphs encode the existence of facts, dependency graphs encode statistical dependencies between random variables.

To avoid problems with cyclical dependencies, it is common to use undirected graphical models, also called Markov Random Fields (MRFs)[12]. A MRF has the following form:

[math]\displaystyle{ P\left(\mathbf{y}_c\vert\boldsymbol{\theta}\right)=\displaystyle \dfrac{1}{Z}\prod_c \psi\left(\mathbf{y}_c\vert\boldsymbol{\theta}\right) }[/math] (29)

where $\psi\left(\mathbf{y}_c\vert\boldsymbol{\theta}\right) \ge 0$is a potential function on the $c$-th subset of variables, in particular the $c$-th clique in the dependency graph, and $Z =\displaystyle\prod_c\psi\left(\mathbf{y}_c\vert\boldsymbol{\theta}\right)$ is the partition function, which ensures that the distribution sums to one. The potential functions capture local correlations between variables in each clique $c$ in the dependency graph. (Note that in undirected graphical models, the local potentials do not have any probabilistic interpretation, unlike in directed graphical models.) This equation again defines a probability distribution over “possible worlds’, i.e., over joint distribution assigned to the random variables $\mathbf{\underline{Y}}$.

The structure of the dependency graph (which defines the cliques in Equation (29)) is derived from a template mechanism that can be defined in a number of ways. A common approach is to use Markov logic[ 126], which is a template language based on logical formulae:

Given a set of formulae $\mathcal{F} = \{F_i\}_{i=1}^L$, we create an edge between nodes in the dependency graph if the corresponding facts occur in at least one grounded formula. A grounding of a formula $F_i$; is given by the (type consistent) assignment of entities to the variables in $F_i$. Furthermore, we define $\psi\left(\mathbf{y}_c\vert\boldsymbol{\theta}\right)$ such that

[math]\displaystyle{ P\left(\mathbf{y}_c\vert\boldsymbol{\theta}\right)=\displaystyle \dfrac{1}{Z}\prod_c \exp\left(\theta_cx_c\right) }[/math] (30)

where $x_c$, denotes the number of true groundings of $F_c$ in $\mathbf{\underline{Y}}$ and $\theta_c$, denotes the weight for formula $F_c$. If $\theta_c > 0$, we prefer worlds where formula $F,_c$ is satisfied; if $\theta_c < 0$, we prefer worlds where formula $F_c$ is violated. If $\theta_c = 0$, then formula $F_c$. is ignored.

To explain this further, consider a KG involving two types of entities, adults and children, and two types of relations, $parentOf$ and $marriedTo$. Figure 6a depicts a sample KG with three adults and one child. Obviously, these relations (edges) are correlated, since people who share a common child are often married, while people rarely marry their own children. In Markov logic, we represent these dependencies using formulae such as:

[math]\displaystyle{ F_1:\left(x,\; parentOf,\;z\right)\wedge (y,\;parentOf, z) \Rightarrow \left(x,\; marriedTo,\; y\right) }[/math]
[math]\displaystyle{ F_2:\left(x,\;mariedTo,\; y\right)\Rightarrow \left(y,\; parentOf,\; x\right) }[/math]

Rather than encoding the rule that adults cannot marry their own children using a formula, we will encode this as a hard constraint into the type system. Similarly, we only allow adults to be parents of children. Thus, there are 6 possible facts in the knowledge graph. To create a dependency graph for this KG and for this set of logical formulae $\mathcal{F}$, we assign a binary random variable to each possible fact, represented by a diamond in Figure 6b, and create edges between these nodes if the corresponding facts occur in grounded formulae $F_1$ or $F_2$. For instance, grounding $F_1$ with $x = a_1$, $y = a_3$, and $z = c$, creates the edges $m_{13} \to p_1c,\; m_{13} \to p_3c$, and $p_1c \to p_3c$. The full dependency graph is shown in Figure 6c.

The process of generating the MRF graph by applying templated rules to a set of entities is known as grounding or instantiation. We note that the topology of the resulting graph is quite different from the original KG. In particular, we have one node per possible KG edge, and these nodes are densely connected. This can cause computational difficulties, as we discuss below.

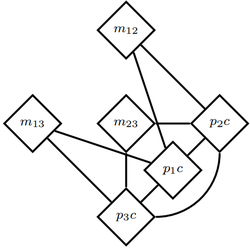
2016 AReviewofRelationalMachineLearn-Fig6a.png 2016 AReviewofRelationalMachineLearn-Fig6b.png 2016 AReviewofRelationalMachineLearn-Fig6c.png
(a) (b) (c)
Figure 6:(a) A small KG. There are 4 entities (circles): 3 adults $(a_1, a_2, a_3)$ and 1 child $c$ There are 2 types of edges: adults may or may not be married to each other, as indicated by the red dashed edges, and the adults may or may not be parents of the child, as indicated by the blue dotted edges. (b) We add binary random variables (represented by diamonds) to each KG edge. (c) We drop the entity nodes, and add edges between the random variables that belong to the same clique potential, resulting in a standard MRF..

==== B. Inference ====

The inference problem consists of estimating the most probable configuration, $y^{\star} = \mathrm{arg\; max}_y p\left(\mathbf{y}|\boldsymbol{\theta}\right)$, or the posterior marginals $p\left(y_i\vert \boldsymbol{\theta}\right)$. In general, both of these problems are computationally intractable [125], so heuristic approximations must be used.

One approach for computing posterior marginals is to use Gibbs sampling (see, or example, [31, 127]) or MC-SAT [128]. One approach for computing the MAP estimate is to use the MPLP (max product linear programming) method [129]. See [125] for more details.

If one restricts the class of potential functions to be just disjunctions (using OR and NOT, but no AND), then one obtains a (special case of) hinge loss MRF (HL-MRFs) [130], for which efficient convex algorithms can be applied, based on a continuous relaxation of the binary random variables. Probabilistic Soft Logic (PSL) [131 provides a convenient form of “syntactic sugar” for defining HL-MRFs, just as MLNs provide a form of syntactic sugar for regular (boolean) MRFs. HL-MRFs have been shown to scale to fairly large knowledge bases [132].

C. Learning

The “learning” problem for MRFs deals with specifying the form of the potential functions (sometimes called “structure learning”’) as well as the values for the numerical parameters $\boldsymbol{\theta}$. In the case of MRFs for KGs, the potential functions are often specified in the form of logical rules, as illustrated above. In this case, structure learning is equivalent to rule learning, which has been studied in a number of published works (see Section V-C and [107, 95]).

The parameter estimation problem (which is usually cast as maximum likelihood or MAP estimation), although convex, is in general quite expensive, since it needs to call inference as a subroutine. Therefore, various faster approximations, such as pseudo likelihood, have been developed (cf. relational dependency networks [133]).

D. Discussion

Although approaches based on MRFs are very flexible, it is in general harder to make scalable inference and devise learning algorithms for this model class, compared to methods based on observable or even latent feature models. In this article, we have chosen to focus primarily on latent and graph feature models because we have more experience with such methods in the context of KGs. However, all three kinds of approaches to KG modeling are useful.

IX. KNOWLEDGE VAULT: RELATIONAL LEARNING FOR KNOWLEDGE BASE CONSTRUCTION

The Knowledge Vault (KV) [28] is a very large-scale automatically constructed knowledge base, which follows the Freebase schema (KV uses the 4469 most common predicates). It is constructed in three steps. In the first step, facts are extracted from a host of Web sources such as natural language text, tabular data, page structure, and human annotations (the extractors are described in detail in [28]). Second, an SRL model is trained on Freebase to serve as a “prior” for computing the probability of (new) edges. Finally, the confidence in the automatically extracted facts is evaluated using both the extraction scores and the prior SRL model.

The Knowledge Vault uses a combination of latent and observable models to predict links in a knowledge graph. In particular, it employs the ER-MLP model (Section IV-D) as a latent feature model and PRA (Section V-C) as a graph feature model. In order to combine the two models, KV uses stacking (Section VI-B). To evaluate the link prediction performance, these models were applied to a subset of Freebase. The ERMLP system achieved an area under the ROC curve (AUCROC) of 0.882, and the PRA approach achieved an almost identical AUC-ROC of 0.884. The combination of both methods further increased the AUC-ROC to 0.911. To predict the final score of a triple, the scores from the combined link-prediction model are further combined with various features derived from the extracted triples. These include, for instance, the confidence of the extractors and the number of (de-duplicated) Web pages from which the triples were extracted. Figure 7 provides a high level overview of the Knowledge Vault architecture.

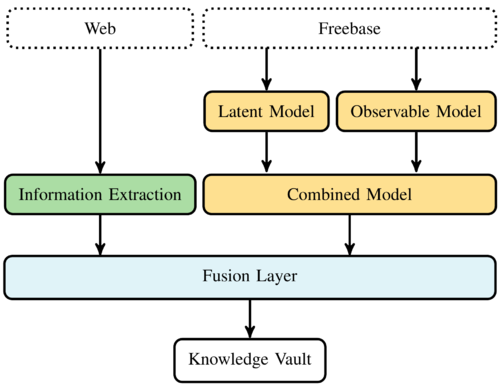
2016 AReviewofRelationalMachineLearn Fig7.png
Figure 7: Architecture of the Knowledge Vault.

Let us give a qualitative example of the benefits of combining the prior with the extractors (i.e., the Fusion Layer in Figure 7). Consider an extracted triple corresponding to the following relation[13]:

(Barry Richter, attended, University of Wisconsin-Madison).

The extraction confidence for this triple (obtained by fusing multiple extraction techniques) is just 0.14, since it was based on the following two rather indirect statements[14]:

In the fall of 1989, Richter accepted a scholarship to the University of Wisconsin, where he played for four years and earned numerous individual accolades ...

and [15]

The Polar Caps’ cause has been helped by the impact of knowledgable coaches such as Andringa, Byce and former UW teammates Chris Tancill and Barry Richter.

However, we know from Freebase that Barry Richter was born and raised in Madison, Wisconsin. According to the prior model, people who were born and raised in a particular city often tend to study in the same city. This increases our prior belief that Richter went to school there, resulting in a final fused belief of 0.61.

Combining the prior model (learned using SRL methods) with the information extraction model improved performance significantly, increasing the number of high confidence triples[16] from 100M (based on extractors alone) to 271M (based on extractors plus prior). The Knowledge Vault is one of the largest applications of SRL to knowledge base construction to date. See [28] for further details.

X. EXTENSIONS AND FUTURE WORK

A. Non-Binary Relations

So far we completely focussed on binary relations; here we discuss how relations of other cardinalities can be handled.

Unary relations: Unary relations refer to statements on properties of entities, e.g., the height of a person. Such data can naturally be represented by a matrix, in which rows represent entities, and columns represent attributes. [64] proposed a joint tensor-matrix factorization approach to learn simultaneously from binary and unary relations via a shared latent representation of entities. In this case, we may also need to modify the likelihood function, so it is Bernoulli for binary edge variables, and Gaussian (say) for numeric features and Poisson for count data (see [134]).

Higher-arity relations: In knowledge graphs, higher-arity relations are typically expressed via multiple binary relations. In Section II, we expressed the ternary relationship playedCharacterIn(LeonardNimoy, Spock, StarTrek-1) via two binary relationships (LeonardNimoy, played, Spock) and (Spock, characterIn, StarTrek-1). However, there are multiple actors who played Spock in different Star Trek movies, so we have lost the correspondence between Leonard Nimoy and StarTrek-1. To model this using binary relations without loss of information, we can use auxiliary nodes to identify the respective relationship. For instance, to model the relationship playedCharacterIn(LeonardNimoy, Spock, StarTrek-1), we can write

subject predicate object
(LeonardNimoy, actor, MovieRole-1)
(MovieRole-I, movie, StarTreck-1)
(MovieRole-1, character, Spock)

where we used the auxiliary entity MovieRole-1 to uniquely identify this particular relationship. In most applications auxiliary entities get an identifier; if not they are referred to as blank nodes. In Freebase auxiliary nodes are called Compound Value Types (CVT).

Since higher-arity relations involving time and location are relatively common, the YAGO2 project extended the SPO triple format to the (subject, predicate, object, time, location)(SPOTL) format to model temporal and spatial information about relationships explicitly, without transforming them to binary relations [27]. Furthermore, there has also been work on extracting higher-arity relations directly from natural language [135].

A related issue is that the truth-value of a fact can change over time. For example, Google’s current CEO is Larry Page, but from 2001 to 2011 it was Eric Schmidt. Both facts are correct, but only during the specified time interval. For this reason, Freebase allows some facts to be annotated with beginning and end dates, using CVT (compound value type) constructs, which represent n-ary relations via auxiliary nodes. In the future, it is planned to extend the KV system to model such temporal facts. However, this is non-trivial, since it is not always easy to infer the duration of a fact from text, since it is not necessarily related to the timestamp of the corresponding source (cf. [136]).

As an alternative to the usage of auxiliary nodes, a set of $n$-th-arity relations can be represented by a single $n+1$-th-order tensor. RESCAL can easily be generalized to higher-arity relations and can be solved by higher-order tensor factorization or by neural network models with the corresponding number of entity representations as inputs [134].

B. Hard Constraints: Types, Functional Constraints, And Others

Imposing hard constraints on the allowed triples in knowledge graphs can be useful. Powerful ontology languages such as the Web Ontology Language (OWL) [137] have been developed, in which complex constraints can be formulated. However, reasoning with ontologies is computationally demanding, and hard constraints are often violated in real-world data [138, 139]. Fortunately, machine learning methods can be robust in the face of contradictory evidence.

Deterministic dependencies: Triples in relations such as subClassOf and is LocatedIn follow clear deterministic dependencies such as transitivity. For example, if Leonard Nimoy was born in Boston, we can conclude that he was born in Massachusetts, that he was born in the USA, that he was born in North America, etc. One way to consider such ontological constraints is to precompute all true triples that can be derived from the constraints and to add them to the knowledge graph prior to learning. The precomputation of triples according to ontological constraints is also called materialization. However, on large knowledge graphs, full materialization can be computationally demanding.

Type constraints: Often relations only make sense when applied to entities of the right type. For example, the domain and the range of marriedTo is limited to entities which are persons. Modelling type constraints explicitly requires complex manual work. An alternative is to learn approximate type constraints by simply considering the observed types of subjects and objects in a relation. The standard RESCAL model has been extended by [74] and [69] to handle type constraints of relations efficiently. As a result, the rank required for a good RESCAL model can be greatly reduced. Furthermore, [85] considered learning latent representations for the argument slots in a relation to learn the correct types from data.

Functional constraints and mutual exclusiveness: Although the methods discussed in Sections IV and V can model long range and global dependencies between triples, they do not explicitly enforce functional constraints that induce mutual exclusivity between possible values. For instance, a person is born in exactly one city, etc. If one of the these values is observed, then observable graph models can prevent other values from being asserted, but if all the values are unknown, the resulting mutual exclusion constraint can be hard to deal with computationally.

C. Generalizing To New Entities And Relations

In addition to missing facts, there are many entities that are mentioned on the Web but are currently missing in knowledge graphs like Freebase and YAGO. If new entities or predicates are added to a KG, one might want to avoid retraining the model due to runtime considerations. Given the current model and a set of newly observed relationships, latent representations of new entities can be calculated approximately in both tensor factorization models and in neural networks, by finding representations that explain the newly observed relationships relative to the current model. Similarly, it has been shown that the relation-specific weights $\mathbf{W}_k$, in the RESCAL model can be calculated efficiently for new relation types given already derived latent representations of entities [140].

D. Querying Probabilistic Knowledge Graphs

RESCAL and KV can be viewed as probabilistic databases (see, e.g., [141, 142]). In the Knowledge Vault, only the probabilities of triples are queried. Some applications might require more complex queries such as: Who is born in Rome and likes someone who is a child of Albert Einstein. It is known that queries involving joins (existentially quantified variables) are expensive to calculate in probabilistic databases ([141]). In [140], it was shown how some queries involving joins can be efficiently handled within the RESCAL framework.

E. Trustworthiness of Knowledge Graphs

Automatically constructed knowledge bases are only as good as the sources from which the facts are extracted. Prior studies in the field of data fusion have developed numerous approaches for modelling the correctness of information supplied by multiple sources in the presence of possible data conflicts (see [143, 144] for recent surveys). However, the key assumption in data fusion — namely, that the facts provided by the sources are indeed stated by them — is often violated when the information is extracted automatically. If a given source contains a mistake, it could be because the source actually contains a false fact, or because the fact has been extracted incorrectly. A recent study [145] has formulated the problem of knowledge fusion, where the above assumption is no longer made, and the correctness of information extractors is modeled explicitly. A follow-up study by the authors [146] developed several approaches for solving the knowledge fusion problem, and applied them to estimate the trustworthiness of facts in the Knowledge Vault (cf. Section IX).

XI. CONCLUDING REMARKS

Knowledge graphs have found important applications in question answering, structured search, exploratory search, and digital assistants. We provided a review of state-of-the-art Statistical relational learning (SRL) methods applied to very large knowledge graphs. We also demonstrated how statistical relational learning can be used in conjunction with machine reading and information extraction methods to automatically build such knowledge repositories. As a result, we showed how to create a truly massive, machine-interpretable “semantic memory” of facts, which is already empowering numerous practical applications. However, although these KGs are impressive in their size, they still fall short of representing many kinds of knowledge that humans possess. Notably missing are representations of “common sense” facts (such as the fact that water is wet, and wet things can be slippery), as well as “procedural” or how-to knowledge (such as how to drive a car or how to send an email). Representing, learning, and reasoning with these kinds of knowledge remains the next frontier for AI and machine learning.

XII. APPENDIX

A. RESCAL is a Special Case of NTN

Here we show how the RESCAL model of Section IV-A is a special case of the neural tensor model (NTN) of Section IV-E. To see this, note that RESCAL has the form

[math]\displaystyle{ f^{RESCAL}_{ijk}=\mathbf{e}^{\top}_i\mathbf{W}_k\mathbf{e}_j=\mathbf{w}_k^{\top}\Big[\mathbf{e}_j\otimes\mathbf{e}_i\Big] }[/math] (31)

Next, note that

[math]\displaystyle{ \mathbf{v}\otimes\mathbf{u}=\mathrm{vec}\left(\mathbf{uv}^{\top}\right)=\Big[\mathbf{u}^{\top}\mathbf{B}^1\mathbf{v}, \cdots, \mathbf{u}^{\top}\mathbf{B}^n\mathbf{v}\Big] }[/math]

where $n = |u||v|$, and $\mathbf{B}^k$ is a matrix of all $0$s except for a single $1$ element in the $k$’th position, which “plucks out” the corresponding entries from the $\mathbf{u}$ and $\mathbf{v}$ matrices. For example,

[math]\displaystyle{ \begin{pmatrix} u_1 \\ u_2\end{pmatrix} \begin{pmatrix} v_1 & v_2\end{pmatrix}= \begin{bmatrix}\begin{pmatrix} u_1 \\ u_2\end{pmatrix}^{\top}\begin{pmatrix} 1 & 0 \\ 0 & 0\end{pmatrix}\begin{pmatrix} v_1 \\ v_2\end{pmatrix}, \cdots,\begin{pmatrix} u_1 \\ u_2\end{pmatrix}^{\top}\begin{pmatrix} 0 & 0 \\ 0 & 1\end{pmatrix}\begin{pmatrix} v_1 \\ v_2\end{pmatrix} \end{bmatrix} }[/math] (32)

In general, define $\delta_{ij}$ as a matrix of all $0$s except for entry $(i,j)$ which is $1$. Then if we define $\mathbf{\underline{B}} = [\delta_{1,1},\cdots,\delta_{H_e},H_e]$ we have

[math]\displaystyle{ \mathbf{h}^b_{ijk}=\Big[\mathbf{e}_i^{\top}\mathbf{B}_k^1\mathbf{e}_j, \cdots, \mathbf{e}^{\top}\mathbf{B}_k^{H_b}\mathbf{e}_j\Big]=\mathbf{e}_j\otimes\mathbf{e}_i }[/math]

Finally, if we define $\mathbf{A}_k$, as the empty matrix (so $\mathbf{h}^a_{ijk}$, is undefined), and $g(u) = u$ as the identity function, then the NTN equation

[math]\displaystyle{ f^{NTN}_{ijk}=\mathbf{w}_k^{\top}g\left(\Big[\mathbf{h}^{a}_{ijk};\mathbf{h}^b_{ijk}\Big]\right) }[/math]

matches Equation 31.

ACKNOWLEDGMENT

Maximilian Nickel acknowledges support by the Center for Brains, Minds and Machines (CBMM), funded by NSF STC award CCF-1231216. Volker Tresp acknowledges support by the German Federal Ministry for Economic Affairs and Energy, technology program “Smart Data” (grant 01MT14001).

Footnotes

References

  • [1] L. Getoor and B. Taskar, Eds., Introduction to Statistical Relational Learning. MIT Press, 2007.
  • [2] S. Dzeroski and N. Lavra¢, Relational Data Mining. Springer Science & Business Media, 2001.
  • [3] L. De Raedt, Logical and relational learning. Springer, 2008.
  • [4] F. M. Suchanek, G. Kasneci, and G. Weikum, “Yago: A Core of Semantic Knowledge,’ in Proceedings of the 16th International Conference on World Wide Web. New York, NY, USA: ACM, 2007, pp. 697-706.
  • [5] S. Auer, C. Bizer, G. Kobilarov, J. Lehmann, R. Cyganiak, and Z. Ives, “DBpedia: A Nucleus for a Web of Open Data,” in The Semantic Web. Springer Berlin Heidelberg, 2007, vol. 4825, pp. 722-735.
  • [6] A. Carlson, J. Betteridge, B. Kisiel, B. Settles, E. R. H. Jr, and T. M. Mitchell, “Toward an Architecture for Never-Ending Language Learning,” in Proceedings of the Twenty-Fourth Conference on Artificial Intelligence (AAAI 2010). AAAT Press, 2010, pp. 1306-1313.
  • [7] K. Bollacker, C. Evans, P. Paritosh, T. Sturge, and J. Taylor, “Freebase: a collaboratively created graph database for structuring human knowledge,” in Proceedings of the 2008 ACM SIGMOD International Conference on Management of data. ACM, 2008, pp. 1247-1250.
  • [8] A. Singhal, “Introducing the Knowledge Graph: things, not strings,” May 2012. [Online]. Available: http://googleblog.blogspot.com/2012/05/ introducing-knowledge- graph-things-not.html
  • [9] G. Weikum and M. Theobald, “From information to knowledge: harvesting entities and relationships from Web sources,” in Proceedings of the twenty-ninth ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems. ACM, 2010, pp. 65-76.
  • [10] J. Fan, R. Hoffman, A. A. Kalyanpur, S. Riedel, F. Suchanek, and P. P. Talukdar, “AKBC-WEKE X: The Knowledge Extraction Workshop at NAACLHLT,’ 2012. [Online]. Available: https://akbcwekex2012. wordpress.com/
  • [11] R. Davis, H. Shrobe, and P. Szolovits, “What is a knowledge representation?” AI Magazine, vol. 14, no. 1, pp. 17-33, 1993.
  • [12] J. EK Sowa, “Semantic networks,’ Encyclopedia of Cognitive Science, 2006.
  • [13] M. Minsky, “A framework for representing knowledge,” MIT-AI Laboratory Memo 306, 1974.
  • [14] T. Berners-Lee, J. Hendler, and O. Lassila, “The Semantic Web,’ 2001. [Online]. Available: http://www. scientificamerican.com/article/the-semantic-web/
  • [15] T. Berners-Lee, “Linked Data - Design Issues,” Jul. 2006. [Online]. Available: http://www.w3.org/DesignIssues/ LinkedData.html
  • [16] C. Bizer, T. Heath, and T. Berners-Lee, “Linked data-the story so far,’ International Journal on Semantic Web and Information Systems, vol. 5, no. 3, pp. 1-22, 2009.
  • [17] G. Klyne and J. J. Carroll, “Resource Description Framework (RDF): Concepts and Abstract Syntax,” Feb. 2004. [Online]. Available: http://www.w3.org/TR/2004/ REC-rdf-concepts-20040210/
  • [18] R. Cyganiak, D. Wood, and M. Lanthaler, “RDF 1.1 Concepts and Abstract Syntax,’ Feb. 2014. [Online]. Available: http://www.w3.org/TR/2014/RECrdf11-concepts-20140225/
  • [19] R. Brachman and H. Levesque, Knowledge Representation and Reasoning. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 2004.
  • [20] J. F. Sowa, Knowledge Representation: Logical, Philosophical and Computational Foundations. Pacific Grove, CA, USA: Brooks/Cole Publishing Co., 2000.
  • [21] Y. Sun and J. Han, “Mining Heterogeneous Information Networks: Principles and Methodologies,” Synthesis Lectures on Data Mining and Knowledge Discovery, vol. 3, no. 2, pp. 1-159, 2012.
  • [22] R. West, E. Gabrilovich, K. Murphy, S. Sun, R. Gupta, and D. Lin, “Knowledge Base Completion via SearchBased Question Answering,” in Proceedings of the 23rd International Conference on World Wide Web, 2014, pp. 515-526.
  • [23] D. B. Lenat, “CYC: A Large-scale Investment in Knowledge Infrastructure,’ Commun. ACM, vol. 38, no. 11, pp. 33-38, Nov. 1995.
  • [24] G. A. Miller, “WordNet: A Lexical Database for English,’ Commun. ACM, vol. 38, no. 11, pp. 39-41, Nov. 1995.
  • [25] O. Bodenreider, ““The Unified Medical Language System (UMLS): integrating biomedical terminology,” Nucleic Acids Research, vol. 32, no. Database issue, pp. D267— 270, Jan. 2004.
  • [26] D. Vrandeci¢é and M. Krotzsch, “Wikidata: a free collaborative knowledgebase,” Communications of the ACM, vol. 57, no. 10, pp. 78-85, 2014.
  • [27] J. Hoffart, F. M. Suchanek, K. Berberich, and G. Weikum, “YAGO2: a spatially and temporally enhanced knowledge base from Wikipedia,” Artificial Intelligence, vol. 194, pp. 28-61, 2013.
  • [28] X. Dong, E. Gabrilovich, G. Heitz, W. Horn, N. Lao, K. Murphy, T. Strohmann, S. Sun, and W. Zhang, “Knowledge Vault: A Web-scale Approach to Probabilistic Knowledge Fusion,” in Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY, USA: ACM, 2014, pp. 601-610.
  • [29] N. Nakashole, G. Weikum, and F. Suchanek, “PATTY: A Taxonomy of Relational Patterns with Semantic Types,” in Proceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning, 2012, pp. 1135-1145.
  • [30] N. Nakashole, M. Theobald, and G. Weikum, “Scalable knowledge harvesting with high precision and high recall,’ in Proceedings of the fourth ACM International Conference on Web search and data mining. ACM, 2011, pp. 227-236.
  • [31] F. Niu, C. Zhang, C. Ré, and J. Shavlik, “Elementary: Large-scale knowledge-base construction via machine learning and statistical inference,’ International Journal on Semantic Web and Information Systems (IJSWIS), vol. 8, no. 3, pp. 42-73, 2012.
  • [32] A. Fader, S. Soderland, and O. Etzioni, “Identifying relations for open information’ extraction,’ in Proceedings of the Conference on Empirical Methods in Natural Language Processing. Stroudsburg, PA, USA: Association for Computational Linguistics, 2011, pp. 1535-1545.
  • [33] M. Schmitz, R. Bart, S. Soderland, O. Etzioni, and others, “Open language learning for information extraction,” in Proceedings of the 2012 Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning. Association for Computational Linguistics, 2012, pp. 523-534.
  • [34] J. Fan, D. Ferrucci, D. Gondek, and A. Kalyanpur, “Prismatic: Inducing knowledge from a large scale lexicalized relation resource,’ in Proceedings of the NAACL HLT 2010 First International Workshop on Formalisms and Methodology for Learning by Reading. Association for Computational Linguistics, 2010, pp. 122-127.
  • [35] B. Suh, G. Convertino, E. H. Chi, and P. Pirolli, "The Singularity is Not Near: Slowing Growth of Wikipedia,” in Proceedings of the 5th International Symposium on Wikis and Open Collaboration. New York, NY, USA: ACM, 2009, pp. 8:1—8:10.
  • [36] J. Biega, E. Kuzey, and F. M. Suchanek, “Inside YAGO2s: A transparent information — extraction architecture,” in Proceedings of the 22Nd International Conference on World Wide Web. Republic and Canton of Geneva, Switzerland: International World Wide Web Conferences Steering Committee, 2013, pp. 325-328.
  • [37] O. Etzioni, A. Fader, J. Christensen, S. Soderland, and M. Mausam, “Open Information Extraction: The Second Generation,’ in Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence - Volume Volume One. Barcelona, Catalonia, Spain: AAAI Press, 2011, pp. 3-10.
  • [38] D. B. Lenat and E. A. Feigenbaum, “On the thresholds of knowledge,” Artificial intelligence, vol. 47, no. 1, pp. 185-250, 1991.
  • [39] R. Qian, “Understand Your World ~~ with Bing, bing search blog,’ Mar. 2013. [Online]. Available: http://blogs.bing.com/search/2013/03/ 2 1/understand- your- world- with-bing/
  • [40] D. Ferrucci, E. Brown, J. Chu-Carroll, J. Fan, D. Gondek, A. A. Kalyanpur, A. Lally, J. W. Murdock, E. Nyberg, J. Prager, and others, “Building Watson: An overview of the DeepQA project,” AI magazine, vol. 31, no. 3, pp. 59-79, 2010.
  • [41] F. Belleau, M.-A. Nolin, N. Tourigny, P. Rigault, and J. Morissette, “Bio2RDF: towards a mashup to build bioinformatics knowledge systems,” Journal of Biomedical Informatics, vol. 41, no. 5, pp. 706—716, 2008.
  • [42] A. Ruttenberg, J. A. Rees, M. Samwald, and M. S. Marshall, “Life sciences on the Semantic Web: the Neurocommons and beyond,” Briefings in Bioinformatics, vol. 10, no. 2, pp. 193-204, Mar. 2009.
  • [43] V. Momtchev, D. Peychev, T. Primov, and G. Georgiev, “Expanding the pathway and interaction knowledge in linked life data,’ Proc. of International Semantic Web Challenge, 2009.
  • [44] G. Angeli and C. Manning, “Philosophers are Mortal: Inferring the Truth of Unseen Facts,” in Proceedings of the Seventeenth Conference on Computational Natural Language Learning. Sofia, Bulgaria: Association for Computational Linguistics, Aug. 2013, pp. 133-142.
  • [45] B. Taskar, M.-F. Wong, P. Abbeel, and D. Koller, “Link Prediction in Relational Data,’ in Advances in Neural Information Processing Systems, S. Thrun, L. Saul, and B. Schélkopf, Eds., vol. 16. Cambridge, MA: MIT Press, 2004.
  • [46] L. Getoor and C. P. Diehl, “Link mining: a survey,” ACM SIGKDD Explorations Newsletter, vol. 7, no. 2, pp. 3-12, 2005.
  • [47] H. B. Newcombe, J. M. Kennedy, S. J. Axford, and A. P. James, “Automatic Linkage of Vital Records Computers can be used to extract "follow-up" statistics of families from files of routine records,’ Science, vol. 130, no. 3381, pp. 954-959, Oct. 1959.
  • [48] S. Tejada, C. A. Knoblock, and S. Minton, “Learning object identification rules for information integration,” Information Systems, vol. 26, no. 8, pp. 607-633, 2001.
  • [49] E. Rahm and P. A. Bernstein, “A survey of approaches to automatic schema matching,’ the VLDB Journal, vol. 10, no. 4, pp. 334-350, 2001.
  • [50] A. Culotta and A. McCallum, “Joint deduplication of multiple record types in relational data,’ in Proceedings of the 14th ACM International Conference on Information and knowledge management. ACM, 2005, pp. 257-258.
  • [51] P. Singla and P. Domingos, “Entity Resolution with Markov Logic,” in Data Mining, 2006. ICDM ’06. Sixth International Conference on, Dec. 2006, pp. 572-582.
  • [52] I. Bhattacharya and L. Getoor, “Collective entity resolution in relational data,’ ACM Trans. Knowl. Discov. Data, vol. 1, no. 1, Mar. 2007.
  • [53] S. E. Whang and H. Garcia-Molina, “Joint Entity Resolution,” in 20/2 IEEE 28th International Conference on Data Engineering. Washington, DC, USA: IEEE Computer Society, 2012, pp. 294-305.
  • [54] S. Fortunato, “Community detection in graphs,’ Physics Reports, vol. 486, no. 3, pp. 75-174, 2010.
  • [55] M. E. J. Newman, “The structure of scientific collaboration networks,’ Proceedings of the National Academy of Sciences, vol. 98, no. 2, pp. 404-409, Jan. 2001.
  • [56] D. Liben-Nowell and J. Kleinberg, “The link-prediction problem for social networks,” Journal of the American society for information science and technology, vol. 58, no. 7, pp. 1019-1031, 2007.
  • [57] D. Jensen and J. Neville, “Linkage and Autocorrelation Cause Feature Selection Bias in Relational Learning,” in Proceedings of the Nineteenth International Conference on Machine Learning. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 2002, pp. 259-266.
  • [58] P. W. Holland, K. B. Laskey, and S. Leinhardt, “Stochastic blockmodels: First steps,” Social networks, vol. 5, no. 2, pp. 109-137, 1983.
  • [59] C. J. Anderson, S. Wasserman, and K. Faust, “Building stochastic blockmodels,’ Social Networks, vol. 14, no. 1-2, pp. 137-161, 1992, special Issue on Blockmodels.
  • [60] P. Hoff, “Modeling homophily and _ stochastic equivalence in symmetric relational data,” in Advances in Neural Information Processing Systems 20. Curran Associates, Inc., 2008, pp. 657-664.
  • [61] J. C. Platt, “Probabilities for SV Machines,’ in Advances in Large Margin Classifiers. MIT Press, 1999, pp. 61-— 74.
  • [62] P. Orbanz and D. M. Roy, “Bayesian models of graphs, arrays and other exchangeable random structures,” JEEE Trans. Pattern Analysis and Machine Intelligence, 2015.
  • [63] M. Nickel, V. Tresp, and H.-P. Kriegel, “A Three-Way Model for Collective Learning on Multi-Relational Data,” in Proceedings of the 28th International Conference on Machine Learning, 2011, pp. 809-816.
  • [64] M. Nickel, V. Tresp, and H.-P. Kriegel, “Factorizing YAGO: scalable machine learning for linked data,” in Proceedings of the 21st International Conference on World Wide Web, 2012, pp. 271-280.
  • [65] M. Nickel, “Tensor factorization for relational learning,” PhD Thesis, Ludwig-Maximilians-Universitat Miinchen, Aug. 2013.
  • [66] Y. Koren, R. Bell, and C. Volinsky, “Matrix factorization techniques for recommender systems,” JEEE Computer, vol. 42, no. 8, pp. 30-37, 2009.
  • [67] T. G. Kolda and B. W. Bader, “Tensor Decompositions and Applications,’ SIAM Review, vol. 51, no. 3, pp. 455-500, 2009.
  • [68] M. Nickel and V. Tresp, “Logistic Tensor-Factorization for Multi-Relational Data,’ in Structured Learning: Inferring Graphs from Structured and Unstructured Inputs (SLG 2013). Workshop at ICML’13, 2013.
  • [69] K.-W. Chang, W.-t. Yih, B. Yang, and C. Meek, “Typed Tensor Decomposition of Knowledge Bases for Relation Extraction,’ in Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing. ACL —- Association for Computational Linguistics, Oct. 2014.
  • [70] S. Kok and P. Domingos, “Statistical Predicate Invention,’ in Proceedings of the 24th International Conference on Machine Learning. New York, NY, USA: ACM, 2007, pp. 433-440.
  • [71] Z. Xu, V. Tresp, K. Yu, and H.-P. Kriegel, “Infinite Hidden Relational Models,” in Proceedings of the 22nd International Conference on Uncertainity in Artificial Intelligence. AUAI Press, 2006, pp. 544-551.
  • [72] C. Kemp, J. B. Tenenbaum, T. L. Griffiths, T. Yamada, and N. Ueda, “Learning systems of concepts with an infinite relational model,’ in Proceedings of the Twenty-First National Conference on Artificial Intelligence, vol. 3, 2006, p. 5.
  • [73] I. Sutskever, J. B. Tenenbaum, and R. R. Salakhutdinov, “Modelling Relational Data using Bayesian Clustered Tensor Factorization,’ in Advances in Neural Information Processing Systems 22, 2009, pp. 1821-1828.
  • [74] D. KrompabB, M. Nickel, and V. Tresp, “Large-Scale Factorization of Type-Constrained Multi-Relational Data,” in Proceedings of the 2014 International Conference on Data Science and Advanced Analytics (DSAA’2014), 2014.
  • [75] M. Nickel and V. Tresp, “Learning Taxonomies from Miulti-Relational Data via Hierarchical LinkBased Clustering,” in Learning Semantics. Workshop at NIPS’11, Granada, Spain, 2011.
  • [76] T. G. Kolda, B. W. Bader, and J. P. Kenny, “Higher-order web link analysis using multilinear algebra,” in Proceedings of the Fifth IEEE International Conference on Data Mining. Washington, DC, USA: IEEE Computer Society, 2005, pp. 242-249.
  • [77] T. Franz, A. Schultz, S. Sizov, and S. Staab, ““Triplerank: Ranking semantic web data by tensor decomposition,” The Semantic Web-ISWC 2009, pp. 213-228, 2009.
  • [78] L. Drumond, S. Rendle, and L. Schmidt-Thieme, “Predicting RDF Triples in Incomplete Knowledge Bases with Tensor Factorization,’ in Proceedings of the 27th Annual ACM Symposium on Applied Computing. Riva del Garda, Italy: ACM, 2012, pp. 326-331.
  • [79] S. Rendle and L. Schmidt-Thieme, “Pairwise interaction tensor factorization for personalized tag recommendation,’ in Proceedings of the third ACM International Conference on Web Search and Data Mining. ACM, 2010, pp. 81-90.
  • [80] S. Rendle, “Scaling factorization machines to relational data,” in Proceedings of the 39th International Conference on Very Large Data Bases. Trento, Italy: VLDB Endowment, 2013, pp. 337-348.
  • [81] R. Jenatton, N. L. Roux, A. Bordes, and G. R. Obozinsky, “A latent factor model for highly multi-relational data,” in Advances in Neural Information Processing Systems .Curran Associates, Inc., 2012, pp. 3167-3175.
  • [82] P. Miettinen, “Boolean Tensor Factorizations,’ in 20/1] IEEE 11th International Conference on Data Mining, Dec. 2011, pp. 447-456.
  • [83] D. Erdos and P. Miettinen, “Discovering Facts with Boolean Tensor Tucker Decomposition,” in Proceedings of the 22nd ACM International Conference on Conference on Information & Knowledge Management. New York, NY, USA: ACM, 2013, pp. 1569-1572.
  • [84] X. Jiang, V. Tresp, Y. Huang, and M. Nickel, “Link Prediction in Multi-relational Graphs using Additive Models.” in Proceedings of International Workshop on Semantic Technologies meet Recommender Systems & Big Data at the ISWC, M. de Gemmis, T. D. Noia, P. Lops, T. Lukasiewicz, and G. Semeraro, Eds., vol. 919. CEUR Workshop Proceedings, 2012, pp. 1-12.
  • [85] S. Riedel, L. Yao, B. M. Marlin, and A. McCallum, “Relation Extraction with Matrix Factorization and Universal Schemas,” in Joint Human Language Technology Conference/Annual Meeting of the North American Chapter of the Association for Computational Linguistics (HLT-NAACL ’/3), Jun. 2013.
  • [86] V. Tresp, Y. Huang, M. Bundschus, and A. Rettinger, “Materializing and querying learned knowledge,” Proc. of IRMLeS, vol. 2009, 2009.
  • [87] Y. Huang, V. Tresp, M. Nickel, A. Rettinger, and H.-P. Kriegel, “A scalable approach for statistical learning in semantic graphs,’ Semantic Web journal SW), 2013.
  • [88] P. Smolensky, “Tensor product variable binding and the representation of symbolic structures in connectionist systems,” Artificial intelligence, vol. 46, no. 1, pp. 159-216, 1990.
  • [89] G. S. Halford, W. H. Wilson, and S. Phillips, “Processing capacity defined by relational complexity: Implications for comparative, developmental, and cognitive psychology,’ Behavioral and Brain Sciences, vol. 21, no. 06, pp. 803-831, 1998.
  • [90] T. Plate, “A common framework for distributed representation schemes for compositional structure,’ Connectionist systems for knowledge representation and deduction, pp. 15-34, 1997.
  • [91] T. Mikolov, K. Chen, G. Corrado, and J. Dean, “Efficient Estimation of Word Representations in Vector Space,” in Proceedings of Workshop at ICLR, 2013.
  • [92] R. Socher, D. Chen, C. D. Manning, and A. Ng, “Reasoning With Neural Tensor Networks for Knowledge Base Completion,” in Advances in Neural Information Processing Systems 26. Curran Associates, Inc., 2013, pp. 926-934.
  • [93] A. Bordes, J. Weston, R. Collobert, and Y. Bengio, “Learning Structured Embeddings of Knowledge Bases,” in Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence, San Francisco, USA, 2011.
  • [94] A. Bordes, N. Usunier, A. Garcia-Duran, J. Weston, and O. Yakhnenko, “Translating Embeddings for Modeling Multi-relational Data,” in Advances in Neural Information Processing Systems 26. Curran Associates, Inc., 2013, pp. 2787-2795.
  • [95] B. Yang, W.-t. Yih, X. He, J. Gao, and L. Deng, “Embedding Entities and Relations for Learning and Inference in Knowledge Bases,’ CoRR, vol. abs/1412.6575, 2014.
  • [96] P. D. Hoff, A. E. Raftery, and M. S. Handcock, “Latent space approaches to social network analysis,” Journal of the American Statistical Association, vol. 97, no. 460, pp. 1090-1098, 2002.
  • [97] L. Lit and T. Zhou, “Link prediction in complex networks: A survey,” Physica A: Statistical Mechanics and its Applications, vol. 390, no. 6, pp. 1150-1170, Mar. 2011.
  • [98] L. A. Adamic and E. Adar, “Friends and neighbors on the Web,” Social Networks, vol. 25, no. 3, pp. 211-230, 2003.
  • [99] A.-L. Barabasi and R. Albert, “Emergence of Scaling in Random Networks,” Science, vol. 286, no. 5439, pp. 509-512, 1999.
  • [100] L. Katz, “A new status index derived from sociometric analysis,’ Psychometrika, vol. 18, no. 1, pp. 39-43, 1953.
  • [101] E. A. Leicht, P. Holme, and M. E. Newman, “Vertex similarity in networks,” Physical Review E, vol. 73, no. 2, p. 026120, 2006.
  • [102] S. Brin and L. Page, “The anatomy of a large-scale hypertextual Web search engine,’ Computer networks and ISDN systems, vol. 30, no. 1, pp. 107-117, 1998.
  • [103] W. Liu and L. Lu, “Link prediction based on local random walk,’ EPL (Europhysics Letters), vol. 89, no. 5, p. 58007, 2010.
  • [104] S. Muggleton, “Inverse entailment and progol,”’ New Generation Computing, vol. 13, no. 3-4, pp. 245-286, 1995.
  • [105] S. Muggleton, “Inductive logic programming,’ New generation computing, vol. 8, no. 4, pp. 295-318, 1991.
  • [106] J. R. Quinlan, “Learning logical definitions from relations,” Machine Learning, vol. 5, pp. 239-266, 1990.
  • [107] L. A. Galarraga, C. Teflioudi, K. Hose, and F. Suchanek, “AMIE: Association Rule Mining Under Incomplete Evidence in Ontological Knowledge Bases,’ in Proceedings of the 22nd International Conference on World Wide Web, 2013, pp. 413-422.
  • [108] L. Galarraga, C. Teflioudi, K. Hose, and F. Suchanek, “Fast rule mining in ontological knowledge bases with AMIE+,” The VLDB Journal, pp. 1-24, 2015.
  • [109] F. A. Lisi, “Inductive logic programming in databases: From datalog to dl+log,’ TPLP, vol. 10, no. 3, pp. 331-359, 2010.
  • [110] C. d’ Amato, N. Fanizzi, and F. Esposito, “Reasoning by analogy in description logics through instance-based learning,” in Proceedings of Semantic Wep Applications and Perspectives. CEUR-WS.org, 2006.
  • [111] J. Lehmann, “DL-learner: Learning concepts in description logics,’ Journal of Machine Learning Research, vol. 10, pp. 2639-2642, 2009.
  • [112] A. Rettinger, U. Loésch, V. Tresp, C. d’Amato, and N. Fanizzi, “Mining the semantic web - statistical learning for next generation knowledge bases,” Data [96] [97] [98] [99] [100] [101] [105] [106] [107] [108] [110] [111] [112] Min. Knowl. Discov., vol. 24, no. 3, pp. 613-662, 2012.
  • [113] U. Loésch, S. Bloehdorn, and A. _ Rettinger, “Graph kernels for rdf data,’ in Proceedings of the 9th International Conference on The Semantic Web: Research and Applications. Berlin, Heidelberg: Springer-Verlag, 2012, pp. 134-148.
  • [114] P. Minervini, C. dAmato, N. Fanizzi, and V. Tresp, “Learning to propagate knowledge in web ontologies,” in 10th International Workshop on Uncertainty Reasoning for the Semantic Web (URSW 2014), 2014, pp. 13-24.
  • [115] N. Lao and W. W. Cohen, “Relational retrieval using a combination of path-constrained random _ walks,’ Machine learning, vol. 81, no. 1, pp. 53-67, 2010.
  • [116] N. Lao, T. Mitchell, and W. W. Cohen, “Random walk inference and learning in a large scale knowledge base,” in Proceedings of the Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, 2011, pp. 529-539.
  • [117] K. Toutanova and D. Chen, “Observed versus latent features for knowledge base and text inference,’ in 3rd Workshop on Continuous Vector Space Models and Their Compositionality, 2015.
  • [118] M. Nickel, X. Jiang, and V. Tresp, “Reducing the Rank in Relational Factorization Models by Including Observable Patterns,” in Advances in Neural Information Processing Systems 27. Curran Associates, Inc., 2014, pp. 1179-1187.
  • [119] Y. Koren, “Factorization Meets the Neighborhood: A Multifaceted Collaborative Filtering Model,’ in Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, NY, USA: ACM, 2008, pp. 426-434.
  • [120] S. Rendle, “Factorization machines with libFM,’ ACM Transactions on Intelligent Systems and Technology (TIST), vol. 3, no. 3, p. 57, 2012.
  • [121] D. H. Wolpert, “Stacked generalization,’ Neural net works, vol. 5, no. 2, pp. 241-259, 1992.
  • [122] L. Bottou, “Large-Scale Machine Learning with Stochastic Gradient Descent,’ in Proceedings of COMPSTAT’2010. — Physica-Verlag HD, 2010, pp. 177-186.
  • [123] K. P. Murphy, Machine learning: a probabilistic per spective. Cambridge, MA: MIT Press, 2012.
  • [124] J. Davis and M. Goadrich, “The Relationship Between Precision-Recall and ROC Curves,” in Proceedings of the 23rd International Conference on Machine learning. ACM, 2006, pp. 233-240.
  • [125] D. Koller and N. Friedman, Probabilistic Graphical Models: Principles and Techniques. MIT Press, 2009.
  • [126] M. Richardson and P. Domingos, “Markov logic networks,” Machine Learning, vol. 62, no. 1, pp. 107—136, 2006.
  • [127] C. Zhang and C. Ré, “Towards high-throughput Gibbs sampling at scale: A study across storage managers,” in Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data. ACM, 2013, pp. 397-408.
  • [128] H. Poon and P. Domingos, “Sound and efficient inference with probabilistic and deterministic dependencies,” in AAAT, 2006.
  • [129] A. Globerson and T. S. Jaakkola, “Fixing Max-Product: Convergent message passing algorithms for MAP LPRelaxations,”’” in NJPS, 2007.
  • [130] S. H. Bach, M. Broecheler, B. Huang, and L. Getoor, “Hinge-loss markov random fields and probabilistic soft logic,” arXiv: 1505.04406 [cs.LG], 2015.
  • [131] A. Kimmig, S. H. Bach, M. Broecheler, B. Huang, and L. Getoor, “A Short Introduction to Probabilistic Soft Logic,” in NIPS Workshop on Probabilistic Programming: Foundations and Applications, 2012.
  • [132] J. Pujara, H. Miao, L. Getoor, and W. W. Cohen, “Using semantics and statistics to turn data into knowledge,” AJ Magazine, 2015.
  • [133] J. Neville and D. Jensen, “Relational dependency net works,” The Journal of Machine Learning Research, vol. 8, pp. 637-652, May 2007.
  • [134] D. Krompaβ, X. Jiang, M. Nickel, and V. Tresp, “Probabilistic Latent-Factor Database Models,” in Proceedings of the 1st Workshop on Linked Data for Knowledge Discovery co-located with European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML PKDD 2014), 2014.
  • [135] H. Li, S. Krause, F. Xu, A. Moro, H. Uszkoreit, and R. Navigli, “Improvement of n-ary relation extraction by adding lexical semantics to distant-supervision rule learning,’ in ICAART 2015 - Proceedings of the 7th International Conference on Agents and Artificial Intelligence. International Conference on Agents and Artificial Intelligence (ICAART-15), 7th, January 10-12, Lisbon, Portugal. SciTePress, 2015.
  • [136] H. Ji, T. Cassidy, Q. Li, and S. Tamang, “Tackling Representation, Annotation and Classification Challenges for Temporal Knowledge Base Population,’ Knowledge and Information Systems, pp. 1-36, Aug. 2013.
  • [137] D. L. McGuinness, F Van Harmelen, and others, “OWL web ontology language overview,’ W3C recommendation, vol. 10, no. 10, p. 2004, 2004.
  • [138] A. Hogan, A. Harth, A. Passant, S. Decker, and A. Polleres, “Weaving the pedantic web,’ in 3rd International Workshop on Linked Data on the Web (LDOW2010), in conjunction with 19th International World Wide Web Conference. Raleigh, North Carolina, USA: CEUR Workshop Proceedings, 2010.
  • [139] H. Halpin, P. Hayes, J. McCusker, D. Mcguinness, and H. Thompson, “When owl: sameAs isn’t the same: An analysis of identity in linked data,’ The Semantic Web-ISWC 2010, pp. 305-320, 2010.
  • [140] D. Krompaβ, M. Nickel, and V. Tresp, “Querying Factorized Probabilistic Triple Databases,’ in The Semantic Web-ISWC 2014. Springer, 2014, pp. 114— 129.
  • [141] D. Suciu, D. Olteanu, C. Re, and C. Koch, Probabilistic Databases. Morgan & Claypool, 2011.
  • [142] D. Z. Wang, E. Michelakis, M. Garofalakis, and J. M. Hellerstein, “BayesStore: managing large, uncertain data repositories with probabilistic graphical models, Proceedings of the VLDB Endowment, vol. 1, no. 1, pp. 340-351, 2008.
  • [143] J. Bleiholder and F Naumann, “Data fusion,’ ACM Comput. Surv., vol. 41, no. 1, pp. 1:1-1:41, Jan. 2009.
  • [144] X. Li, X. L. Dong, K. Lyons, W. Meng, and D. Srivastava, “Truth finding on the deep web: Is the problem solved?” Proceedings of the VLDB Endowment, vol. 6, no. 2, pp. 97-108, Dec. 2012.
  • [145] X. L. Dong, E. Gabrilovich, G. Heitz, W. Horn, K. Murphy, S. Sun, and W. Zhang, “From data fusion to knowledge fusion,” Proceedings of the VLDB Endowment, vol. 7, no. 10, pp. 881-892, Jun. 2014.
  • [146] X. L. Dong, E. Gabrilovich, K. Murphy, V. Dang, W. Horn, C. Lugaresi, S. Sun, and W. Zhang, “Knowledge-based trust: Estimating the trustworthiness of web sources,” Proceedings of the VLDB Endowment, vol. 8, no. 9, pp. 938-949, May 2015.

BibTeX

@article{2016_AReviewofRelationalMachineLearn,
  author    = {Maximilian Nickel and
               Kevin Murphy and
               Volker Tresp and
               Evgeniy Gabrilovich},
  title     = {A Review of Relational Machine Learning for Knowledge Graphs},
  journal   = {Proceedings of the IEEE},
  volume    = {104},
  number    = {1},
  pages     = {11--33},
  year      = {2016},
  url       = {https://doi.org/10.1109/JPROC.2015.2483592},
  doi       = {10.1109/JPROC.2015.2483592},
}


 AuthorvolumeDate ValuetitletypejournaltitleUrldoinoteyear
2016 AReviewofRelationalMachineLearnEvgeniy Gabrilovich
Kevin P. Murphy
Volker Tresp
Maximilian Nickel		A Review of Relational Machine Learning for Knowledge Graphs2016
  1. ↑ For detailed statistics, see http://www.mpi-inf.mpg.de/departments/databases-and-information-systems/research/yago-naga/yago/statistics/.
  2. ↑ http://thenoisychannel.com/2011/11/15/cikm-2011-industry-eventjohngiannandrea-on-freebase-a-rosetta-stone-for-entities
  3. ↑ Non-redundant triples, see [28, Table 1]
  4. ↑ Last published numbers: https://tools.wmflabs.org/wikidata-todo/stats.php and https://www.wikidata.org/wiki/Category:All_Properties.
  5. ↑ English content, Version 2014 from http://wiki.dbpedia.org/data-set-2014
  6. ↑ See [ 27, Table 5]
  7. ↑ Last published numbers: http://insidesearch.blogspot.de/2012/12/getsmarter-answers-from-knowledge_4.html
  8. ↑ As an example, there are currently 10,306 male and 7,586 female American actors listed in Wikipedia, while there are only 1,268 male and 1,354 female Indian, and 77 male and no female Nigerian actors. India and Nigeria, however, are the largest and second largest film industries in the world.
  9. ↑ ALS stands for Alternating Least-Squares
  10. ↑ The relations edu-start, edu-end, job-start, job-end represent the start and end dates of attending an educational institution and holding a particular job, respectively.
  11. ↑ [85 considered an additional term $f_{ijk}^{UNI}:=f_{ijk}^{ADD}+\mathbf{w}_k^{\top}\phi_{ij}^{SUB+OBJ}$ , where $\phi_{ij}^{SUB+OBJ}i$ object pairs. is a (non-composite) latent feature representation of subject-object pair
  12. ↑ Technically, since we are conditioning on some observed features $\mathbf{x}$, this is a Conditional Random Field (CRF), but we will ignore this distinction.
  13. ↑ For clarity of presentation we show a simplified triple. Please see [28] for the actually extracted triples including compound value types (CVT).
  14. ↑ Source: http://www.legendsofhockey.net/LegendsOfHockey/jsp/SearchPlayer.jsp?player=1_1377
  15. ↑ Source: —_ http://host.madison.com/sports/high-school/hockey/numbersdwindling-for-once-mighty-madison-high-school-hockey-programs/article_ 95843e00-ec34-11df-9da9-001cc4c002e0.html
  16. ↑ Triples with the calibrated probability of correctness above 90%.
Retrieved from "http://www.gabormelli.com/RKB/index.php?title=2016_AReviewofRelationalMachineLearn&oldid=865565"